Summary
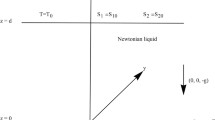
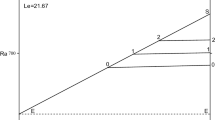
The onset of convection in a fluid layer with an internal heat source is studied. In addition to the temperature field there are present two different, dissolved salt fields. Thus, this paper investigated the effect of an internal heat source on the problem of triply-diffusive convection. The effect of the boundary conditions is found to be important. For two surfaces free of tangential stress a disconnected oscillatory neutral curve can be found which has the same minimum as the stationary convection one. Thus the possibility of simultaneous initiation of convection by two different mechanisms, but with two different aspect ratios, is found. It is also found that the above effect is prsent when the lower surface is fixed while the upper surface is free of tangential stress, even if the container of the fluid is of finite horizontal extent. When both surfaces are fixed we have not observed the twin minima effect.
Similar content being viewed by others
References
Chen, C. F., Su, T. F.: Effect of surface tension on the onset of convection in a double-diffusive layer. Phys. FluidsA 4, 2360–2367 (1992).
Corriel, S. R., McFadden, G. B., Voorhees, P. W., Sekerka, R. F.: Stability of a planar interface solidification of a multicomponent system. J. Crystal Growth82, 300–313 (1987).
Drazin, P. G., Reid, W. H.: Hydrodynamic stability. Cambridge: Cambridge University Press 1981.
Guo, J. L., Kaloni, P. N.: Nonlinear stability problem of a rotating double-diffusive porous layer. J. Math. Anal. Appl.190, 373–390 (1995).
Guo, J. L., Kaloni, P. N.: Double-diffusive convection in a porous medium, nonlinear stability, and the Brinkman effect. Stud. Appl. Math.94, 341–358 (1995).
Guo, J. L., Qin, Y., Kaloni, P. N.: Nonlinear stability problem of a rotating doubly diffusive fluid layer. Int. J. Eng. Sci.104, 173–200 (1995).
Hutter, K., Strughan, B.: Penetrative convection in thawing subsea permafrost. Cont. Mech. Thermodyn.9, 259–272 (1997).
Kaloni, P. N., Guo, J. L.: Steady nonlinear double-diffusive convection in a porous medium based upon the Brinkman-Forchheimer model. J. Math. Anal. Appl.204, 138–155 (1996).
Lopez, A. R., Romero, L. A., Pearlstein, A. J.: Effect of rigid boundaries on the onset of convective instability in a triply diffusive fluid layer. Phys. FluidsA 2, 897–902 (1990).
Matthews, P. C.: A model for the onset of penetrative covection. J. Fluid Mech.188, 571–583 (1988).
McKenzie, D. P., Roberts, J. M., Weiss, N. O.: Convection in the Earth' mantle: towards a numerical solution. J. Fluid Mech.62, 465–538 (1974).
Mielke, A.: Mathematical analysis of sideband instabilities with application to Rayleigh-Bénard convection. J. Nonlin. Sci.7, 57–99 (1997).
Moroz, I. M.: Multiple instabilities in a triply diffusive system. Stud. Appl. Math.80, 137–164 (1989).
Mulone, G.: On the nonlinear stability of a fluid layer of a mixture heated and salted from below. Cont. Meth. Thermodyn.6, 161–184 (1994).
Noulty, R. A., Leaist, D. G.: Quarternary diffusion in aqueous KCl−K2PO4−H3PO4 mixtures. J. Phys. Chem.91, 1655–1658 (1987).
Payne, L. E., Song, J. C., Straughan, B.: Double diffusive porous penetrative convection-thawing subsea permaforst. Int. J. Eng. Sci.26, 797–809 (1988).
Pearlstein, A. J., Harris, R. M., Terrones, G.: The onset of convective instability in a triply diffusive fluid layer. J. Fluid Mech.202, 443–465 (1989).
Roberts, P. H.: Convection in horizontal layers with internal heat generation. Theory J. Fluid Mech.30, 33–49 (1967).
Rosenblat, S., Homsy, G. M., Davis, S. H.: Nonlinear Marangoni convection in bounded layers. Part 2. Rectangular cylindrical containers. J. Fluid Mech.120, 123–138 (1982).
Straughan, B.: The energy method, stability and nonlinear convection. Springer Ser. in Appl. Math. Sci. (1992).
Straughan, B.: Mathematical aspects of penetrative convection. Harlow: Longman 1993.
Straughan, B., Walker, D. W.: Anisotropic porous penetrative convection. Proc R. Soc. London Ser.A 452, 97–115 (1966).
Straughan, B., Walker, D. W.: Multi-component convection-diffusion and penetrative convection. Fluid Dyn. Res.19, 77–89 (1997).
Tracey, J.: Multi-component convection-diffusion in a porous medium. Cont. Mech. Thermodyn.8, 361–381 (1996).
Tracey, J.: Stability analyses of multi-component convection-diffusion problems. Ph.D. Thesis, University of Glasgow 1997.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Straughan, B., Tracey, J. Multi-component convection-diffusion with internal heating or cooling. Acta Mechanica 133, 219–238 (1999). https://doi.org/10.1007/BF01179019
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01179019