Skip to main content
Springer Nature Link
Log in

Viscous dissipation effects on thermal entrance region heat transfer in pipes with uniform wall heat flux

  • Published:
Applied Scientific Research Aims and scope Submit manuscript

Abstract

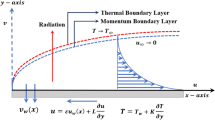
The analytical solution to Graetz problem with uniform wall heat flux is extended by including the viscous dissipation effect in the analysis. The analytical solution obtained reduces to that of Siegel, Sparrow and Hallman neglecting viscous dissipation as a limiting case. The sample developing temperature profiles, wall and bulk temperature distributions and the local Nusselt number variations are presented to illustrate the viscous dissipation effects. It is found that the role of viscous dissipation on thermal entrance region heat transfer is completely different for heating and cooling at wall. In the case of cooling at wall, a critical value of Brinkman number, Br c=−11/24, exists beyond which (−11/24<Br<0) the fluid bulk temperature will always be less than the uniform entrance temperature indicating the predominance of cooling effect over the viscous heating effect. On the other hand, with Br < Br c the bulk temperature T b will approach the wall temperature T w at some downstream position and from there onward the bulk temperature T b becomes less than the wall temperature T w with T w > B b > T 0 indicating overall heating effect for the fluid. The numerical results for the case of cooling at wall Br < 0 are believed to be of some interest in the design of the proposed artctic oil pipeline.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Abbreviations

Br :

Brinkman number, μU 2m /kT c=Pr Ec

C n , D n , K n :

coefficients in the series expansion of θ, equation (13)

C p :

specific heat at constant pressure

Ec :

Eckert number, U 2m /C p T c

h :

local heat transfer coefficient

k :

thermal conductivity

Nu :

local Nusselt number, (2R 0) h/k

P :

axial pressure

Pr :

Prandtl number, C p μ/k

q w :

uniform wall heat flux per unit area

R, X :

radial and axial coordinates

Re :

Reynolds number, (2R 0) U m/ν

R 0 :

pipe radius

r, x :

dimensionless radial and axial coordinates, R/R 0, X/R 0 Re Pr

T, T b, T 0, T w :

fluid temperature, bulk temperature, uniform fluid temperature at entrance and wall temperature, respectively

T c :

characteristic temperature, q w R 0/k

U, U m :

fluid velocity and mean fluid velocity in X direction

u :

dimensionless axial velocity, U/2 U m=(1−r 2)

Y n :

eigenfunctions of equation (10)

β n :

eigenvalues of equation (10)

θ :

dimensionless temperature difference defined in equation (6)

θ :

dimensionless temperature difference, (T−T 0)/T c

θ b :

bulk temperature, 4 ∝ 10 θur dr

θ w :

wall temperature (T w−T 0)/T c

μ :

absolute viscosity

ν :

kinematic viscosity

ρ :

fluid density

References

  1. Jakob, M., Heat Transfer, Vol. 1, p. 451, John Wiley, New York, 1956.

    Google Scholar 

  2. Sellars, J. R., M. Tribus, and J. S. Klein, Trans. Am. Soc. Mech. Engrs. 78 (1956) 441.

    Google Scholar 

  3. Siegel, R., E. M. Sparrow, and T. M. Hallman, Appl. Sci. Res. A 7 (1958) 386.

    Article  MATH  MathSciNet  Google Scholar 

  4. Hsu, C.-J., Appl. Sci. Res. 17 (1967) 359.

    Article  MATH  Google Scholar 

  5. Hsu, C.-J., A.I.Ch.E. J. 17 (1971) 732.

    Google Scholar 

  6. Brinkman, H. C., Appl. Sci. Res. A 2 (1951) 120.

    Article  Google Scholar 

  7. Bird, R. B., W. E. Steward, and E. N. Lightfoot, Transport Phenomena, p. 296, John Wiley, New York, 1960.

    Google Scholar 

  8. Nelson, W. L., Petroleum Refinery Engineering, Appendix B, McGraw-Hill, New York, 1958.

    Google Scholar 

  9. Ou, J. W. and K. C. Cheng, Submitted for publication.

Download references

Author information

Authors and Affiliations

  1. Dept. of Mech. Eng., University of Alberta, Edmonton, Alberta, Canada

    J. W. Ou & K. C. Cheng

Authors
  1. J. W. Ou
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. K. C. Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ou, J.W., Cheng, K.C. Viscous dissipation effects on thermal entrance region heat transfer in pipes with uniform wall heat flux. Appl. Sci. Res. 28, 289–301 (1973). https://doi.org/10.1007/BF00413074

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00413074

Keywords