Abstract
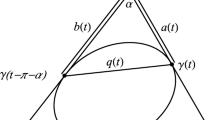
Suppose that two distinct plane convex bodies have the same Steiner symmetrals about a finite number n of given lines. Then we obtain an upper bound for the measure of their symmetric difference. The bound is attained if, and only if, the directions of the lines are equally spaced and the bodies are two regular concentric polygons, with n sides, each obtained from the other by rotation through an angle π/n. This result follows from a new isoperimetric inequality for convex polygons.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Davison, M. and Grünbaum, F, ‘Tomographic Reconstruction with Arbitrary Directions’, Comm. Pure Appl. Math. 34 (1981), 77–120.
Falconer, K. J., ‘X-Ray Problems for Point Sources’, Proc. London Math. Soc. (3) 46 (1983), 241–262.
Falconer, K. J., ‘Hammer's X-Ray Problem and the Stable Manifold Theorem’, J. London Math. Soc. (2) 28 (1983), 149–160.
Falconer, K. J., ‘On the Equireciprocal Point Problems’, 14 (1983), 113–126.
Gardner, R. J. and McMullen, P., ‘On Hammer's X-Ray Problem’, J. London Math. Soc. (2) 21, (1980), 171–175.
Gardner, R. J., ‘Symmetrals and X-rays of Planar Convex Bodies’, Archiv. Math. 41 (1983), 183–189.
Giering, O., ‘Bestimming von Eibereichen un Eikörpern durch Steiner-Symmetrisierungen’, Sber. Bayer. Akad. Wiss. München, Math.-Nat. Kl. (1962), 225–253.
Hammer, P. C., ‘Problem 2’, Proc. Symp. in Pure Mathematics, Vol. VII, Convexity, American Mathematical Society, 1963.
Madych, W. R., ‘Degree of Approximation in Computerized Tomography’ in E. W. Cheney (ed.), Approximation Theory, III, Academic Press, New York, 1980.
Madych, W. R. and Nelson, S. A., ‘Polynomial Based Algorithms for Computed Tomography’, SIAM J. Appl. Math. 43 (1983), 157–185.
Shepp, L. A. and Logan, B. F., ‘The Fourier Reconstruction of a Head Section’, IEEE Trans. Nucl. Sci., NS 21, (1974), 21–43.
Shepp, L. A., ‘Computed Tomography’, Proc. Symp. in applied Mathematics, 27, American Math. Soc., Cincinnati, 1982.
Volčič, A., ‘Ghost Convex Bodies’ (to appear in Boll. Un. Mat. Ital.).
Volčič, A., ‘Well-Posedness of the Gardner-McMullen Reconstruction Problem’, Proc. Conf. on Measure theory, Oberwolfach 1983, Springer Lecture Notes in Mathematics.
Volčič, A., ‘A Three Point Solution to Hammer's X-ray Problem’ (to appear).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Longinetti, M. An isoperimetric inequality for convex polygons and convex sets with the same symmetrals. Geom Dedicata 20, 27–41 (1986). https://doi.org/10.1007/BF00149270
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00149270