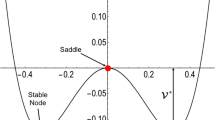
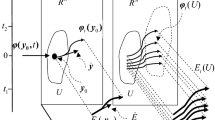
Abstract
The purpose of this paper is to provide a brief summary of the various analytical predictive criteria in order for “strange phenomena” to occur in a class of softening nonlinear oscillators, oscillators which may exhibit escape from a potential well. Implications of Melnikov's criteria are discussed first and transient chaos in the twin-well potential oscillator is illustrated. Three different heuristic criteria for steady state chaos or escape solution, proposes by F. Moon, G. Schmidt and W. Szemplińskia-Stupnicka, are then presented and compared to computer simulation results.
Similar content being viewed by others
References
Ueda, Y., ‘Steady motions exhibited by Duffing's equation: A picture book of regular and chaotic motions’, in New Approaches to Nonlinear Problems in Dynamics, ed. P.J.Holmes, SIAM, Philadelphia, 1980, pp. 331–322.
Ueda, Y., ‘Randomly transitional phenomena in the system governed by Duffing's equation, J. Stat. Phys. 20, 1979, 181–196.
Ueda, Y., ‘Survey of regular and chaotic phenomena in the forced Duffing oscillator’, Chaos, Solitons and Fractals 1, 1991, 199–231.
Moon, F.C., ‘Experiments on chaotic motion of a forced nonlinear oscillator—strange attractors‘, ASME J. Appl. Mech. 47, 1980, 648–644.
Moon, F.C., Chaotic Vibrations, J. Wiley & Sons, New York, 1987.
Szemplińska-Stupnicka, W., ‘Secondary resonances and approximate models of routes to chaotic motions in non-linear oscillators’, J. Sound and Vib. 113, 1987, 155–172.
Szemplińska-Stupnicka, W. and Niezgodzki, P., ‘The approximate approach to chaos phenomena in oscillators having single equilibrium position’, J. Sound and Vib. 141, 1990, 181–192.
Leung, A.Y.T. and Fung, T.C., ‘Construction of chaotic regions’, J. Sound and Vib. 131, 1989, 445–455.
Benedettini, F. and Rega, G., ‘Periodic solutions leading to chaos in an oscillator with quadratic and cubic nonlinearity’, Intern. Series of Numerical Mathematics 97, 1991, 115–120.
Rega, G., Benedettini, F., and Salvatori, A., ‘Periodic and chaotic motion of an unsymmetrical oscillator in nonlinear structural dynamics’, Chaos, Solitons and Fractals 1, 1991, 39–54.
Nayfeh, A.H. and Sanchez, N.E., ‘Bifurcations in a forced softening Duffing oscillator’, Int. J. Non-Linear Mech. 24, 1989, 483–497.
Zavodney, L.D., Nayfeh, A.H., and Sanchez, N.E., ‘Bifurcations and chaos in parametrically excited single-degree-of-freedom systems’, Nonlinear Dynamics 1, 1990, 1–21.
Tang, D.M. and Dowell, E.H., ‘On the threshold force for chaotic motions for a forced buckled beam’, J. Appl. Mech. 55, 1988, 190–196.
Thompson, J.M.T., ‘Loss of engineering integrity due to the erosion of absolute and transient basin boundaries’, in Nonlinear Dynamics in Engineering Systems, ed. W.Schiehlen, Springer-Verlag, Berlin, 1990, pp. 313–320.
Thompson, J.M.T., ‘Chaotic phenomena triggering the escape from a potential well’, Proc. R. Soc. London A 421, 1989, 195–225.
Szemplińska-Stupnicka, W., Plaut, R.H., and Hsieh, J.C., ‘Period doubling and chaos in unsymmetric structures under parametric excitation’, J. Appl. Mech. 56, 1989, 947–952.
Szemplińska-Stupnicka, W., ‘Cross-well chaos and escape phenomena in driven oscillators’, Nonlinear Dynamics 3, 1992, 225–243.
Szemplińska-Stupnicka, W. and Rudowski, J., ‘Local methods in predicting occurrence of chaos in two-well potential systems: superharmonic frequency region’, J. Sound and Vib. 152, 1992, 57–72.
Dowell, E.H. and Pezeshki, C., ‘On necessary and sufficient conditions for chaos to occur in Duffing's equation: an heuristic approach’, J. Sound and Vib. 121, 1988, 195–200.
Dowell, E.H., ‘Chaotic oscillations in mechanical systems’, Computational Mech. 3, 1988, 199–216.
Szemplińska-Stupnicka, W., ‘A discussion on necessary and sufficient conditions for steady state chaos’, J. Sound and Vib. 152, 1992, 369–372.
Guckenheimer, J. and Holmes, P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer-Verlag, New York, 1983.
Koch, B.P. and Leven, R.D., ‘Subharmonic and homoclinic bifurcations in a parametrically forced pendulum’, Physica D 16, 1985, 4–13.
Bishop, S.R., Mathematical and computational modeling for the design of pipe bend and compliant systems, Ph.D. Thesis, Polytechnic of North London, 1987.
Schmidt, G., ‘Onset of chaos and global analytical solutions for Duffing's oscillator’, ZAMM 16, 1986, 129–140.
Schmidt, G. and Dum, R., ‘Van der Pol-Duffing oscillators an trigonometric iteration’, ZAMM 69, 1989, 267–274.
Huberman, B.A. and Crutchfield, J.P., ‘Chaotic states of anharmonic system in periodic fields’, Phys. Rev. Letters 43, 1979, 1743–1747.
Räty, R., Isomaki, H.M., and Boëhm, J., ‘Chaotic motion of a classical anharmonic oscillator’, Acta Politechn. Scand. Me 85, 1984, 1–30.
Räty, R., vonBoëhm, J., and Isomaki, H.M., ‘Absence of inversion-symmetric limit cycles of even periods and the chaotic motion of Duffing's oscillator’, Phys. Letters 103A, 1984, 289–291.
Szemplińska-Stupnicka, W., The Behavior of Nonlinear Vibrating Systems, Kluwer Academic Press, Dordrecht, London, Vol I and II, 1990.
Szemplińska-Stupnicka, W., ‘The approximate analytical methods in the study of transition to chaotic motion in nonlinear oscillators’, in Engineering Applications of Dynamics of Chaos, eds. W.Szemplińska and H.Troger, Springer Verlag, Wien, 1991.
Szemplińska-Stupnicka, W. and Rudowski, J., ‘Bifurcations phenomena in a nonlinear oscillator: Approximate analytical studies versus computer simulation results’, Physica D (in print).
Virgin, L.N., ‘On the harmonic response of an oscillator with unsymmetric restoring force’, J. Sound and Vib. 126, 1988, 157–166.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Szemplińska-Stupnicka, W. The analytical predictive criteria for chaos and escape in nonlinear oscillators: A survey. Nonlinear Dyn 7, 129–147 (1995). https://doi.org/10.1007/BF00053705
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00053705