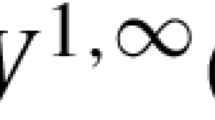Abstract
These notes are devoted to a summary on the mean-field limit of large ensembles of interacting particles with applications in swarming models. We first make a summary of the kinetic models derived as continuum versions of second order models for swarming. We focus on the question of passing from the discrete to the continuum model in the Dobrushin framework. We show how to use related techniques from fluid mechanics equations applied to first order models for swarming, also called the aggregation equation. We give qualitative bounds on the approximation of initial data by particles to obtain the mean-field limit for radial singular (at the origin) potentials up to the Newtonian singularity. We also show the propagation of chaos for more restricted set of singular potentials.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
Bibliography
M. Agueh, R. Illner, and A. Richardson, Analysis and simulations of a refined flocking and swarming model of Cucker-Smale type, Kinetic and Related Models 4:1–16, 2011.
L.A. Ambrosio, N. Gigli, and G. Savaré, Gradient flows in metric spaces and in the space of probability measures, Lectures in Mathematics, Birkhäuser, 2005.
G. Albi, L. Pareschi, Modelling self-organized systems interacting with few individuals: from microscopic to macroscopic dynamics, Applied Math. Letters, 26:397–401, 2013.
I. Aoki, A Simulation Study on the Schooling Mechanism in Fish, Bull. Jap. Soc. Sci. Fisheries 48:1081–1088, 1982.
D. Balagué, and J. A. Carrillo, Aggregation equation with growing at infinity attractive-repulsive potentials, Proceedings of the 13th International Conference on Hyperbolic Problems, Series in Contemporary Applied Mathematics CAM 17, Higher Education Press, 1:136–147, 2012.
D. Balagué, Carrillo, T. J. A., Laurent, and G. Raoul, Nonlocal interactions by repulsive-attractive potentials: radial ins/stability, to appear in Physica D, 2013.
D. Balagué, Carrillo, T. J. A., Laurent, and G. Raoul, Dimensionality of Local Minimizers of the Interaction Energy, to appear in Arch. Rat. Mech. Anal., 2013.
A. Barbaro, K. Taylor, P. F. Trethewey, L. Youseff, and B. Birnir, Discrete and continuous models of the dynamics of pelagic fish: application to the capelin, M ath. and Computers in Simulation, 79:3397–3414, 2009.
A. L. Bertozzi and T. Laurent, Finite-time blow-up of solutions of an aggregation equation in Rn , Comm. Math. Phys., 274:717–735, 2007.
A. L. Bertozzi, J. A. Carrillo, and T. Laurent, Blowup in multidimensional aggregation equations with mildly singular interaction kernels, N onlinearity, 22:683–710, 2009.
A. L. Bertozzi, T. Laurent, and J. Rosado, Lp theory for the multidimensional aggregation equation, Comm. Pure Appl. Math., 43:415–430, 2010.
A. L. Bertozzi, T. Laurent, and F. Léger, Aggregation and spreading via the newtonian potential: the dynamics of patch solutions, M athematical Models and Methods in Applied Sciences, 22(supp01):1140005, 2012.
M. Bodnar, J.J.L. Velazquez, Friction dominated dynamics of interacting particles locally close to a crystallographic lattice, accepted in Math. Methods Appl. Sci., 2012.
E. Boissard, Simple bounds for convergence of empirical and occupation measures in 1-Wasserstein distance, Electron. J. Probab. 16:2296–2333, 2011.
E. Boissard, Problémes d’interaction discret-continu et distances de Wasserstein, Thesis, http://thesesups.ups-tlse.fr/1389/, 2011.
F. Bolley, J. A. Cañizo, and J. A. Carrillo Stochastic mean-field limit: non-Lipschitz forces & swarming, Math. Mod. Meth. Appl. Sci., 21:2179-2210, 2011.
F. Bolley, A. Guillin, and C. Villani, Quantitative concentration inequalities for empirical measures on non-compact spaces, Probab. Theory Related Fields, 137:541–593, 2007.
W. Braun and K. Hepp, The Vlasov Dynamics and Its Fluctuations in the 1/N Limit of Interacting Classical Particles, Commun. Math. Phys., 56:101–113, 1977.
M. Burger, P. Markowich, and J. Pietschmann, Continuous limit of a crowd motion and herding model: Analysis and numerical simulations, Kinetic and Related Methods, 4:1025–1047, 2011.
S. Camazine, J.-L. Deneubourg, N. R. Franks, J. Sneyd, G. Theraulaz, and E. Bonabeau, Self-Organization in Biological Systems, Princeton University Press, 2003.
J.A. Cañizo, J.A. Carrillo, and J. Rosado, Collective Behavior of Animals: Swarming and Complex Patterns, Arbor, 186:1035–1049, 2010.
J.A. Cañizo, J.A. Carrillo, and J. Rosado : A well-posedness theory in measures for some kinetic models of collective motion, M ath. Mod. Meth. Appl. Sci., 21:515–539, 2011.
J. A. Carrillo, M. Di Francesco, A. Figalli, T. Laurent, and D. Slepčev, Global-in-time weak measure solutions and finite-time aggregation for nonlocal interaction equations, Duke Math. J., 156:229–271, 2011.
J. A. Carrillo, M. Di Francesco, A. Figalli, T. Laurent, and D. Slepčev, Confinement in nonlocal interaction equations, N onlinear Anal., 75(2):550–558, 2012.
J. A. Carrillo, M. R. D’Orsogna, and V. Panferov, Double milling in selfpropelled swarms from kinetic theory, Kinetic and Related Models 2:363-378, 2009.
J.-A. Carrillo, M. Fornasier, J. Rosado, and G. Toscani, Asymptotic Flocking Dynamics for the kinetic Cucker-Smale model, SIAM J. Math. Anal., 42:218–236, 2010.
J.A. Carrillo, M. Fornasier, G. Toscani, and F. Vecil, Particle, Kinetic, and Hydrodynamic Models of Swarming, Mathematical Modeling of Collective Behavior in Socio-Economic and Life Sciences, Series: Modelling and Simulation in Science and Technology, Birkhauser, pages 297-336, 2010.
J.A. Carrillo, A. Klar, S. Martin, and S. Tiwari, Self-propelled interacting particle systems with roosting force, M ath. Mod. Meth. Appl. Sci., 20:1533–1552, 2010.
J. A. Carrillo, V. Panferov, S. Martin, A new interaction potential for swarming models, to appear in Physica D, 2013.
J.A. Carrillo, R.J. McCann, and C. Villani, Kinetic equilibration rates for granular media and related equations: entropy dissipation and mass transportation estimates, Rev. Matemática Iberoamericana, 19:1–48, 2003.
J.A. Carrillo, R.J. McCann, and C. Villani, Contractions in the 2-Wasserstein length space and thermalization of granular media, Arch. Rat. Mech. Anal., 179:217–263, 2006.
T. Champion, L. D. Pascale, and P. Juutinen, The ∞-Wasserstein distance: local solutions and existence of optimal transport maps, SIAM J. Math. Anal., 40:1–20, 2008.
I. D. Couzin, J. Krause, N. R. Franks, and S. A. Levin, Effective leadership and decision making in animal groups on the move, N ature 433:513–516, 2005.
F. Cucker and S. Smale, Emergent behavior in flocks, I EEE Trans. Automat. Control 52:852-862, 2007.
C. De Lellis and L. Székelyhidi, The Euler equations as a differential inclusion, Ann. of Math. 170:1417–1436, 2009.
R. Dobrushin, Vlasov equations, Funct. Anal. Appl. 13:115–123, 1979.
M. R. D’Orsogna, Y. L. Chuang, A. L. Bertozzi, and L. Chayes, Selfpropelled particles with soft-core interactions: patterns, stability, and collapse, Phys. Rev. Lett. 96, 2006.
R. Eftimie, G. de Vries, and M.A. Lewis, Complex spatial group patterns result from different animal communication mechanisms, Proceedings of the National Academy of Sciences, 104:6974–6979, 2007.
N. Fournier, M. Hauray, and S. Mischler, Propagation of chaos for the 2D viscous vortex model, preprint http://arxiv.org/abs/1212.1437
I. Gallagher, L. St-Raymond, and B. Texier, From Newton to Boltzmann: hard spheres and short-range potentials, preprint http://arxiv.org/abs/1208.5753
C. R. Givens and R. M. Shortt, A class of Wasserstein metrics for probability distributions, M ichigan Math. J., 31(2):231–240, 1984.
F. Golse, The Mean-Field Limit for the Dynamics of Large Particle Systems, Journées équations aux dérivées partielles, 9:1–47, 2003.
J. Goodman, T. Hou, and J. Lowengrub Convergence of the point vortex method for the 2-D Euler equations, Comm. Pure Appl. Math. 43:415–430, 1990.
C. Graham, and S. Méléard, Stochastic particle approximations for generalized Boltzmann models and convergence estimates, The Annals of Probability, 25:115–132, 1997.
S.-Y. Ha, J.-G. Liu, A simple proof of the Cucker-Smale flocking dynamics and mean-field limit, Commun. Math. Sci. 7 (2) (2009) 297–325.
S.-Y. Ha and E. Tadmor, From particle to kinetic and hydrodynamic descriptions of flocking, Kinetic and Related Models 1:415–435, 2008.
J. Haskovec, Flocking dynamics and mean-field limit in the Cucker-Smaletype model with topological interactions, preprint, 2013.
M. Hauray, Wasserstein distances for vortices approximation of Euler-type equations, M ath. Mod. Meth. Appl. Sci., 19:1357–1384, 2009.
M. Hauray and P.-E. Jabin, Particles approximations of Vlasov equations with singular forces : Propagation of chaos, preprint.
M. Hauray and S. Mischler. On Kac’s chaos and related problems, preprint.
C. K. Hemelrijk and H. Hildenbrandt, Self-Organized Shape and Frontal Density of Fish Schools, Ethology 114, 2008.
A. Huth and C. Wissel, The Simulation of the Movement of Fish Schools, J. Theo. Bio., 1992.
M. Kac, Foundations of kinetic theory, I n Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, 1954–1955, vol. III (Berkeley and Los Angeles, 1956), University of California Press, pp. 171–197.
H. P. Mckean, An exponential formula for solving Boltzmann’s equation for a Maxwellian gas, J. Combinatorial Theory, 2:358–382, 1967.
H. P. Mckean, The central limit theorem for Carleman’s equation, I srael J. Math., 21:54–92, 1975.
T. Kolokonikov, H. Sun, D. Uminsky, and A. Bertozzi. Stability of ring patterns arising from 2d particle interactions, Physical Review E, 84:015203, 2011.
O.E. III. Lanford Time evolution of large classical systems. Lecture Notes in Phys. 38, Springer Verlag 1975, p. 1–111.
T. Laurent, Local and global existence for an aggregation equation, Communications in Partial Differential Equations, 32:1941–1964, 2007.
H. Levine, W.-J. Rappel and I. Cohen, Self-organization in systems of selfpropelled particles, Phys. Rev. E, 63:017101-1/4, 2000.
Y. X. Li, R. Lukeman, and L. Edelstein-Keshet, Minimal mechanisms for school formation in self-propelled particles, Physica D, 237:699–720, 2008.
R. J. McCann, Stable rotating binary stars and fluid in a tube, H ouston J. Math., 32(2):603–631, 2006.
A. Majda and A.L. Bertozzi, Vorticity and Incompressible Flow, Cambridge Texts in Applied Mathematics, Cambridge University Press, United Kingdom, 2002.
C. Marchioro and M. Pulvirenti, Mathematical theory of incompressible nonviscous fluids, Applied Mathematical Sciences 96, Springer-Verlag, New York, 1994.
S. Méléard, Asymptotic behaviour of some interacting particle systems; McKean-Vlasov and Boltzmann models, In Probabilistic models for nonlinear partial differential equations (Montecatini Terme, 1995), Lecture Notes in Math. 1627. Springer, Berlin, 1996.
S. Mischler and C. Mouhot, Kac’s program in kinetic theory, to appear in Inventiones mathematicae, 2013.
A. Mogilner and L. Edelstein-Keshet, A non-local model for a swarm, J. Math. Bio., 38:534–570, 1999.
A. Mogilner, L. Edelstein-Keshet, L. Bent, and A. Spiros, Mutual interactions, potentials, and individual distance in a social aggregation, J. Math. Biol., 47:353–389, 2003.
H. Neunzert, An introduction to the nonlinear Boltzmann-Vlasov equation, In Kinetic theories and the Boltzmann equation (Montecatini Terme, 1981), Lecture Notes in Math. 1048. Springer, Berlin, 1984.
H. Osada, Propagation of chaos for the two-dimensional Navier-Stokes equation, In Probabilistic methods in mathematical physics (Katata/Kyoto, 1985), Academic Press, Boston, 1987, 303–334.
F. Otto, The geometry of dissipative evolution equations: the porous medium equation, Comm. Partial Differential Equations 26:101–174, 2001.
J. Parrish, and L. Edelstein-Keshet, Complexity, pattern, and evolutionary trade-offs in animal aggregation, Science, 294: 99–101, 1999.
L. Perea, G. Gómez, P. Elosegui, Extension of the cucker–smale control law to space flight formations, AIAA Journal of Guidance, Control, and Dynamics, 32:527–537, 2009.
S. Schochet, The point-vortex method for periodic weak solutions of the 2-D Euler equations, Comm. Pure Appl. Math. 49:911–965, 1996.
H. Spohn, Large scale dynamics of interacting particles, Texts and Monographs in Physics, Springer, 1991.
A.-S. Sznitman, Topics in propagation of chaos, In Ecole d’Eté de Probabilités de Saint-Flour XIX 1989, Lecture Notes in Math. 1464. Springer, Berlin, 1991.
C.M. Topaz and A.L. Bertozzi, Swarming patterns in a two-dimensional kinematic model for biological groups, SIAM J. Appl. Math., 65:152–174, 2004.
C.M. Topaz, A.L. Bertozzi, and M.A. Lewis, A nonlocal continuum model for biological aggregation, Bulletin of Mathematical Biology, 68:1601–1623, 2006.
T. Vicsek, A. Czirok, E. Ben-Jacob, I. Cohen, and O. Shochet, Novel type of phase transition in a system of self-driven particles, Phys. Rev. Lett., 75:1226–1229, 1995.
C. Villani, Limite de champ moyen, Lecture notes, 2002.
C. Villani, Topics in optimal transportation, volume 58 of Graduate Studies in Mathematics, American Mathematical Society, Providence, RI, 2003.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 CISM, Udine
About this chapter
Cite this chapter
Carrillo, J.A., Choi, YP., Hauray, M. (2014). The derivation of swarming models: Mean-field limit and Wasserstein distances. In: Muntean, A., Toschi, F. (eds) Collective Dynamics from Bacteria to Crowds. CISM International Centre for Mechanical Sciences, vol 553. Springer, Vienna. https://doi.org/10.1007/978-3-7091-1785-9_1
Download citation
DOI: https://doi.org/10.1007/978-3-7091-1785-9_1
Publisher Name: Springer, Vienna
Print ISBN: 978-3-7091-1784-2
Online ISBN: 978-3-7091-1785-9
eBook Packages: EngineeringEngineering (R0)