Improving Performance of Convolutional Neural Networks by Separable Filters on GPU

Abstract

Convolutional neural networks (CNNs) are one of the most successful deep architectures in machine learning. While they achieve superior recognition rate, the intensive computation of CNNs limits their applicability. In this paper, we propose a method based on separable filters to reduce the computational cost. By using Singular Value Decompositions (SVDs), a 2D filter in the CNNs can be approximated by the product of two 1D filters, and the 2D convolution can be computed via two consecutive 1D convolutions. We implemented a batched SVD routine on GPUs that can compute the SVD of multiple small matrices simultaneously, and three convolution methods using different memory spaces according to the filter size. Comparing to the state-of-art GPU implementations of CNNs, experimental results show that our methods can achieve up to 2.66 times speedup in the forward pass and up to 2.35 times speedup in the backward pass.

1 Introduction

Deep learning has gained popularity recently in machine learning owing to its great recognition ability. The success of deep learning lies in its hierarchical features composition, which constructs features hierarchically from low levels to higher ones. By which, one can obtain more useful features for learning than that of “shallow learning”. Architectures or models that utilize this concept are called deep architectures.

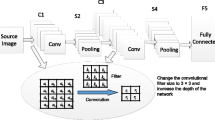
Among various deep architectures, convolutional neural networks (CNNs), proposed by LeCun et al. [16], achieve superior recognition ability, especially for images [26]. CNNs exploit the idea of hierarchical features composition by a sequence of convolutions and pooling operations, followed by classification operations such as logistic regressions [16, 26] or SVMs [20, 24]. Many industrial applications were built based on CNNs, for example, the face recognition systems of Google and Facebook [15, 23], and the search engine of Baidu [10].

One drawback of CNNs is their high computational cost. There are some approaches to accelerate the training speed. Glorot et al. used a biologically plausible activation function called rectified linear unit (ReLU), which converges faster than the commonly used sigmoid logistic and tanh activation functions [8]. Mamalet et al. proposed a method to combine the convolutions with the average pooling operations which leads to $1.6 \times$ speedup [18]. Mathieu et al. performed convolutions in Fourier domain through FFTs and achieve $3 \times$ speedup [19]. Cuda-convnet and Caffe drastically shortened the training time by using well-optimized GPU codes [1, 13].

In this paper, we propose a method based on the separable filters to improve the performance convolution calculation on GPU. If a 2D filter is a rank 1 matrix of dimension $p \times q$, it can be decomposed into a product of two 1D filters [22], and the computation cost is decreased by a factor of $(pq/(p+q))$ theoretically. Many works have utilized this idea to accelerate the performance of CNNs, such as [5, 12, 17, 21, 25]. However, how to implement separable filters on GPU for better performance is still under investigation.

The implementation of separated filters on GPU requires two kernels. One is to decompose the separated filters and the other is to compute two 1D convolutions consecutively. We used singular value decomposition (SVD) to obtain the approximation and implemented a batched SVD kernel. For the computation of convolutions, we designed three implementations that use different memory spaces. The performance of those methods are varied for different filter sizes.

The contributions of this paper are summarized as follows:

• Design and implement batched SVD kernel on GPU.

• Design and implement GPU kernels to compute consecutive 1D filters.

• Analyze the performance and recognition accuracy of CNNs using approximate separable filters.

The rest of this paper is organized as follows. The notation and background knowledge including the architecture of CNNs in is introduced in Sect. 2. In Sect. 3, the SVD approximation algorithm and the proposed method are illustrated. In Sect. 4, the details of our GPU implementations are described. Experiment results are presented in Sect. 5. In Sect. 6, conclude and future work are given.

2 Background

2.1 Convolutional Neural Networks

Neural networks (NNs) are powerful models for machine learning due to their capability of learning nonlinear and complex mappings from input data to outputs. In [16], convolutional neural networks (CNNs) have been widely applied to image processing nowadays. CNNs perform a sequence of convolutions and pooling operations to extract features, which are then served as the input to classification operations such as logistic regressions and SVMs.

The convolution is an important operation in image processing field, which can be used to detect edges, to blur images, to sharpen details, etc. The convolution of two matrices $X \in \mathbb {R}^{m \times n}$ and $F \in \mathbb {R}^{p \times q}$ is $Y = X \otimes F$, where X is called the input and F is called the filter.

After convolutions, the pooling layer takes place. It summarizes a small subset of the input by taking their maximum or average. The outputs of the pooling layer are the features invariant to shifts because the same results will always be obtained no matter where the specific values are located in the pooling region.

CNNs construct deep architectures by stacking multiple stages, each of which consists of one convolutional layer and one pooling layer. There is an additional classification layer in the final stage, and the nonlinear activation functions are usually applied element-wisely between two stages [4].

2.2 Separable Filters

A 2D filter is separable if it can be expressed as an outer product of two vectors, so that a 2D convolution operation is equal to the combination of two 1D convolutions. The following proof is based on [22]. Let Y and X be $m \times n$ matrices and F be a $p \times q$ filter. By the definition of 2D convolution:

$$\begin{aligned} Y&= X \otimes F, \nonumber \\ y_{i,j}&= \sum _{k=-\frac{p}{2}}^{\frac{p}{2}} \sum _{l=-\frac{q}{2}}^{\frac{q}{2}} x_{i+k, j+l} \cdot f_{k,l}, \end{aligned}$$

(1)

where $x_{i,j}=0$ for $i<0, i\ge m$ and $j<0, j\ge n$.

Suppose an $p\times q$ matrix $F=uv^T$, where u and v are vectors of length p and q respectively. The element $f_{k,l}$ in F can be expressed as

$$\begin{aligned} f_{k,l}&= u_k \cdot v_l. \end{aligned}$$

(2)

By substituting (2) into (1) we can get:

(3)

Equation (3) first convolves X with v, and then convolves again with u. This equals to perform two 1D convolutions.

2.3 Singular Value Decomposition

In linear algebra, the singular value decomposition (SVD) is a decomposition of a matrix having the form:

$$\begin{aligned} A = U \varSigma V^T \end{aligned}$$

(4)

where A is an $m \times n$ matrix and $m \ge n$, U is an $m \times m$ orthogonal matrix, V is an $n \times n$ orthogonal matrix, and $\varSigma$ is an $m \times n$ diagonal matrix. The diagonal elements of $\varSigma$ are called singular values and are sorted in the descending order. If A has rank r, the tailing $(n-r)$ entries are zeros. The m columns of U are the left singular vectors while the n columns of V are the right singular vectors.

The SVD can be used to obtain the low rank matrix approximation. Let $\varSigma _k$ be a diagonal matrix that keeps the first k entries and zeros out the last $(r-k)$ entries in $\varSigma$. By multiplying $\varSigma _k$ with U and V, we obtain a truncated matrix $A_k = U \varSigma _k V^T$. Let B be any matrix with rank k. It can be shown that

$$\begin{aligned} \left\| A-A_k \right\| _F \le \left\| A-B \right\| _F, \end{aligned}$$

where $\left\| \cdot \right\| _F$ denotes Frobenius norm of matrices. This shows that the error between A and $A_k$ is smaller than the error between A and any other matrix B with rank k [6].

Alternatively, the SVD can be viewed as a weighted sum of rank 1 matrices. Let $u_i$ and $v_i$ be the i-th column of U and V respectively, and $\sigma _i$ be the i-th entry along the diagonal of $\varSigma$. Equation (4) can be rewritten as $A = \sum _{i=1}^{r} \sigma _i u_i v^{T}_{i}$.

3 Algorithms

3.1 Filters Approximated by SVD

A 2D filter is separable into two 1D filters if it is a rank 1 matrix. But most 2D filters in CNNs are unlikely to be rank 1. As a result, we use the SVD decomposition to generate rank 1 matrices to approximate the filters, which is the well-known problem low rank matrix approximation. The common approaches to solve SVD are the Jacobi Algorithm and the Golub Kahan Algorithm [9], which are implemented in many LAPACK libraries [3, 7]. Since we only interest in the rank 1 matrix approximation, the Power Method is used to decompose the matrix [9].

The power method is used to find the largest eigenvalue in magnitude and the corresponding eigenvector of a matrix. The power method performs refinements iteratively to approximate the largest eigenvalue in magnitude. The convergence rate is $\left| \frac{\lambda _1}{\lambda _0} \right|$, where $\lambda _0$ and $\lambda _1$ are the largest and the second largest eigenvalues in magnitude [9].

Let F be a $p \times p$ filter (assume all filters in CNNs are square.), and be decomposed into $F = U \varSigma V^T$. By pre-multiplying $F^T$ to F, we obtain $F^TF = V \varSigma ^2 V^T$, which can be applied through the power method to find the largest eigenvalue $\lambda _0$ and the corresponding eigenvector $v_0$, i.e. the singular value $\sigma _0 = \sqrt{\lambda _0}$, and the right singular vector. The left singular vector $u_0$ can be obtained by $u_0 = \frac{1}{\sigma _0} Fv_0$. The algorithm is provided in Algorithms 1 and 2.

3.2 CNNs Training Based on Separable Filters

The standard backpropagation algorithm consists of a forward pass and a backward pass. In the forward pass, it approximates 2D filters by two 1D filters as shown in Algorithm 2, and performs two 1D convolutions. In the backward pass, it reuses computed 1D filters to perform two 1D convolutions as well. The approximations are computed once in one batch (or mini-batch) iteration, and it is computed again when the filters (parameters) are updated.

To apply rotations to 1D filters, we have to flip the row filters in left/right direction and flip the column filters in up/down direction.

4 GPU Implementations

This section presents the GPU implementations based on cuda-convnet. Two major kernels are focused: batched SVDs and separable convolutions.

4.1 Batched SVDs

There are many GPU accelerated LAPACK libraries, such as CULA [11] and MAGMA [2], capable of computing SVDs. However, they are designed to parallelize over one problem with rather large size (more than $1000 \times 1000$). What needed in CNN is to solve many (several hundreds) but small (usually less than $15 \times 15$) SVDs simultaneously. Furthermore, we only need the largest singular value and the corresponding singular vectors. Other libraries do not meet those requirements.

We implemented the batched SVDs based on Algorithm 2 and assign each SVD problem to one block in the GPU. Some considerations relating to performance are addressed. First, there are several matrix-matrix and matrix-vector multiplications involved. Their data can be completely stored in the shared memory for fast computation because of their small dimensions. Second, in Algorithm 1, the number of iterations required for convergence are different among filters. It is unsatisfied that we have to wait for a few of the SVDs to converge while most of them are already finished. Therefore, in addition to the termination criterion stated in Algorithm 1, we set an upper limit for the number of iterations which stops the SVD computations no matter whether they are converged or not.

Third, the initialization of the vector $b_0$ in Algorithm 1 is an important factor for the convergence. A vector that is close to the eigenvector requires less iterations than those of a vector that is far from it. We can initialize $b_0$ to be the eigenvector in the previous batch iteration for fast convergence, since the eigenvector in this batch iteration is more close to that in the previous batch iteration than to a random vector.

Fig. 1.

An example illustrating the tile and the halo region.

4.2 Separable Convolutions

We implemented the separable convolutions by the tiling algorithm which proceeds as follows.

• 1. Divide the input into several small tiles to fit each of them into the fast but small memory.

• 2. Perform the convolutions in parallel.

• 3. Store the results to the destinations (the slow memory).

In the step 1, in addition to loading input data within the tile region, we have to load the “halo region” of the half of the filter size outside of the tile region. As can be seen in Fig. 1, the larger the filter size, the more the number of memory accesses are required. Therefore, we have implemented three versions which utilize different memory spaces according to their filter sizes: register-based method, one-pass method, and two-pass method.

Register-Based Method. For small filter, it is possible to load the whole data (the tile and the halo region) into the register file, which is the fastest but least memory and is only private to its thread. We load all data into the register file and let every thread perform convolutions in parallel. Because the register file cannot be indexed dynamically at runtime, we hardcode the filter sizes by using C++ templates, which allow the same code to be compiled for different sizes according to compile-time parameters. Below shows the partial code:

One-Pass Method. For larger filters, the whole data cannot fit into the register file and will cause the exceeding data be spilled into the slow memory. Thus, the one-pass method loads the data into the shared memory in which the data can be shared among the block. This method proceeds as follows.

• 1. Load all data into the shared memory.

• 2. Perform the first convolutions in parallel.

• 3. Store the intermediate results to the shared memory.

• 4. Wait until all threads are finished.

• 5. Perform the second convolutions with the intermediate results.

• 6. Store the final results to the destinations.

The above steps are similar to that of the register-based method. The major difference is the synchronization in the step 4. It has to wait all intermediate results are correctly stored in the shared memory because they are required for the second convolutions.

Two-Pass Method. In the one-pass method, a larger filter implies a larger halo region, which accounts for more memory accesses and the operation counts. The two-pass method solves this problem by breaking the computation in the one-pass method into two independent computations, which are

• 1. Computation 1:

  • (a) Load data into the shared memory.

  • (b) Perform the first convolutions in parallel.

  • (c) Store the intermediate results to the slow memory.

• 2. Computation 2:

  • (a) Load the intermediate results into the shared memory.

  • (b) Perform the second convolutions in parallel.

  • (c) Store the final results to the destinations.

The two computations are identical except that they take different input data. There is no explicit synchronization between the two computations and an additional memory is required to store the intermediate results. Figure 2 illustrates one-pass method and two-pass method pictorially.

Fig. 2.

Comparison of one-pass method and two-pass method.

Comparison of Three Implementations. Let the size of tile be $m\times m$ and the size of filter be $p\times p$. Table 1 compares the number of memory accesses and operation counts of three implementations of separable filter and the traditional 2D convolution.

Table 1. Comparison of memory accesses and operation counts of three implementations of separable filters and traditional 2D convolution.

5 Experiments

This section reports the evaluation results of the speed and the recognition accuracy for the proposed methods. All experiments were performed on the NVIDIA Tesla K20m GPU which has 5 GB memory and 2496 cores. Computation time is measured in milliseconds.

5.1 Evaluation of SVD Approximations

We report the computation time of our method by performing 1024 SVDs for different matrix sizes. We have set the relative error to be $10^{-6}$ and the max number of iterations to be to 100. As can be seen in Table 2, there are less than 20 % of the SVDs not converged under the limit. Without this limit, the computation time was increased because some SVDs required thousands of iterations to converge. The computation time can be further reduced by using the eigenvector in the previous batch iterations as the initial vector. This reduced the computation time by 27 % $\sim$ 77 % as the size increases.

Table 2. Average number of iterations of batched SVD.

5.2 Evaluation of CNNs

We first compared the speed of our method with the original cuda-convnet and then compared the recognition accuracy.

Evaluation of Speed. The speed of the three implementations are compared with various filter sizes. For all experiments, we used 64 feature maps for both of the input and output. These settings are typical configurations in CNNs. The tile size is $16\times 16$, which means each feature map has 16 tiles.

Figure 3 shows the computation time for the forward pass. For small filter sizes (less than 5), the register-based method is the fastest, but it slows down rapidly as the filter size increases. For the one-pass and the two-pass method, the computation time is increased more smoothly comparing to the register-based method. They are faster when the filter size is larger than 7. But overall, the separated filters methods are faster than cuda-convnet, which implements 2D convolutions. For the forward pass, the speedup is up to 2.66 times; and for the backward pass, the speedup is up to 2.35 times.

Fig. 3.

Speed of the forward pass comparison with respect to the filter size.

Evaluation of Recognition Accuracy. We evaluated the proposed method for image classification with the CIFAR-10 dataset [14]. CIFAR-10 consists of 60000 $32\times 32$ color images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 testing images. The 10 classes are airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck.

We construct two CNNs with different architectures. The first architecture (layers-18pct.cfg) consists of 3 convolutional layers, each of which followed by a pooling layer, and a logistic regression layer. All of the convolutional layers have filter size 5, and the input and output feature maps are 3 and 32, 32 and 32, 32 and 64 for the first, the second, and the third convolutional layer. The second architecture (layers-conv-local-11pct.cfg) consists of 4 convolutional layers, 2 pooling layers followed by the first 2 convolutional layers, and a logistic regression layer. The first 2 convolutional layers have filter size 5 and the last convolutional layers have filter size 3. The input and output feature maps are 3 and 64, 64 and 64, 64 and 64, 64 and 32 respectively. The experimental results are shown in the Table 3. Only slight accuracy degradation are observed when the sparable filter methods are used.

Table 3. Comparison of classification accuracy.

6 Conclusion

In this paper, we proposed a performance improving method for training CNNs based on separable filters. First, by using the SVDs, the 2D filters in the convolutional layers can be approximated by the product of two 1D filters. Then, these approximated 1D filters were used to perform two 1D convolutions, which reduces the computation cost. We presented a batched SVDs that can compute multiple small matrices simultaneously, and three methods which used different memory spaces according to the filter size. For small filter sizes, it was possible to load the entire data into the register file to efficiently compute the convolutions. For large filter sizes, we used the tiled algorithm to compute the convolutions in the shared memory. Our method achieved $1.38\times \sim 2.66\times$ speedup in the forward and the backward pass. The overall training time could be reduced by 13 % with 1 % drop in the recognition accuracy.

Table 4. Percentage of the largest singular value in all singular values.

Because only the rank 1 filter approximations are used in our method, though a large speedup is achieved,the error also becomes large as the filter size increases. Table 4 shows the percentage of the largest singular values in the summation of all singular values for different filter sizes. In the future work, we will explore the higher rank filter approximation which can reduce the computation cost while sustain the recognition accuracy. One direction will be the use of multi-GPU in which multiple rank 1 filters are computed to form the full rank filters. Another direction is to combine the FFT method in [19] with our method.