The Variant of Remote Set Problem on Lattices

Abstract

In 2015, Haviv proposed the Remote Set Problem ($RSP$) on lattices and gave a deterministic algorithm to find a set containing a point which is $O(\sqrt{k/n})$ far from the lattice in $\ell _{p}$ norm for $2\le p\le \infty$, where n is the lattice rank and k divides n. Inspired by it, we propose the variant of Remote Set Problem on Lattices (denoted by V-RSP) that only depends on parameter $\gamma \le 1$. We obtain that the complexity classes that $V-RSP$ belong to with the change of parameter $\gamma$. Using some elementary tools, we can solve $V-RSP$ that can find a set containing a point which is O(k / n) far from the lattice in any $\ell _{p}$ norm for $1\le p\le \infty$. Furthermore, we also study relationships between $\ell _{2}$ distance from a point to a lattice $\varvec{\mathcal {L}}$ and covering radius ($\rho ^{(p)}(\varvec{\mathcal {L}})$), where $\rho ^{(p)}(\varvec{\mathcal {L}})$ is defined with respect to the $\ell _{p}$ norm for $1\le p\le \infty$, here, for $p=\infty$, our proof does not rely on Komlós Conjecture.

1 Introduction

A lattice is a discrete additive subgroup of $\mathbb {R}^{m}$ and is the set of all integer linearly combinations of n linearly independent vectors $\varvec{b}_{1},\ldots ,\varvec{b}_{n}$ in $\mathbb {R}^{m}$, where n is the rank of the lattice, m is the dimension of the lattice and $\varvec{b}_{1},\ldots ,\varvec{b}_{n}$ is called a lattice basis. Gauss [7] gave an algorithm to find the shortest vector in any two dimension lattice that originated the study of lattices. Since then, many different lattice problems were proposed. In 1996, Ajtai [2] showed that finding relatively short nonzero vectors is as hard as approximating shortest vector problems in the worst case in a family of random lattice. These random lattices can be used for cryptography. Hence, the study of lattices gains a lot of attention from a computational point of view.

There are two classical problems in lattices. The first is the Shortest Vector Problem ($SVP$): given a lattice, find the shortest non-zero lattice vector. The second is the Closest Vector Problem ($CVP$): given a lattice and a target vector, find the closest lattice vector to the target vector.

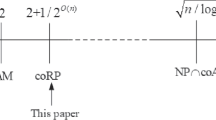
The covering radius $\rho ^{(p)}(\varvec{\mathcal {L}})$ of lattice $\varvec{\mathcal {L}}$ is the maximum $\ell _{p}$ distance of a point in the linear span of $\varvec{\mathcal {L}}$ from the lattice, where $\rho ^{(p)}(\varvec{\mathcal {L}})$ is measured with respect to the $\ell _{p}$ norm for $1\le p\le \infty$. The covering radius problem is to find $\rho ^{(p)}(\varvec{\mathcal {L}})$ for a given lattice $\varvec{\mathcal {L}}$. The Covering Radius Problem ($CRP$) is also an important lattice problem and the exact $CRP$ is in $\varPi _{2}$ at the second level of the polynomial hierarchy. Computing the covering radius of a lattice is a classic problem in geometry of numbers, but it has received so far little attention from an algorithmic point of view. In 2004, Micciancio [16] showed that finding collision of some hash function can be reduced to approximate $CRP$ of lattices, where $CRP$ only is used to connect the average and worst case complexity of lattice problems. Motivated by [8], Guruswami et al. [10] initiated the study of computation complexity for $CRP$, and showed that $CRP _{2}$ lies in AM, $CRP _{\sqrt{n/\log n}}$ lies in coAM and $CRP _{\sqrt{n}}$ lies in $NP\cap coNP$ which implies that under Karp reductions $CRP _{\sqrt{n}}$ is not NP-hard unless $NP=coNP$. But they did not give some hardness results for $CRP$ [10]. Peikert [18] showed that $CRP _{\sqrt{n}}$ lies in coNP in the $\ell _{p}$ norm for $2\le p\le \infty$. The first hardness result for $CRP$ was presented by Haviv and Regev, they proved that there exists some constant such that it is $\varPi _{2}$-hard in the $\ell _{p}$ norm for any sufficiently large value of p [12]. In 2015, Haviv [13] proposed the Remote Set Problem ($RSP$) on lattices which can be viewed as a generalized search variant of $CRP$. The goal of $RSP$ is to find a set of points containing a point which is far from the lattice under a deterministic algorithm in $\ell _{p}$ norm for $2\le p\le \infty$. By the deterministic polynomial time algorithm for $RSP$, Haviv showed that $CRP _{\sqrt{n/\log n}}$ lies in NP which improved the factor from [10], and proved that approximation $GAPCRP$ can be reduced to approximation $GAPCVP$.

In the study of $CRP$, we usually find a point whose distance from the lattice approximates the covering radius. There is a deterministic construction of all the $M^{n}$ linear combinations of the n basis vectors with all coefficients in $\{0,1/M,\ldots ,1-1/M\}$ where M is an integer. Micciancio [10] showed that there exists at least one of them whose distance from the lattice approximates the covering radius to within a factor of $1-1/M$. In order to decrease the number of exponential points in the above construction [10], Haviv proposed $RSP$ and gave a deterministic algorithm (see Sect. 3) that outputs $n/k\cdot 2^{k}$ linear combinations of vectors in basis with coefficient in $\{0,1/2\}$ (i.e. $M=2$) by partitioning the n basis vectors into n / k sets of size k [13]. The algorithm outputs a set of $n/k\cdot 2^{k}$ points containing a point whose $\ell _{p}$ distance from a lattice is at least $1/(2c_{p})\cdot \sqrt{k/n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ for $2\le p<\infty$, where $c_{p}$ is a constant. For $p=\infty$, there is a similar result. Haviv analyzed $RSP$ with respect to Banach spaces and obtained the results which hold for any $\ell _{p}$ norm for $2\le p\le \infty$. Here, we will consider the variant of Remote Set Problem which is denoted by $V$-$RSP$ with respect to any $\ell _{p}$ norm for $1\le p\le \infty$.

Our Contributions. In this paper, we consider the variant of Remote Set Problem ($V-RSP$) on lattices. Using elementary method, we prove that $V-RSP$ can be adapted to any $\ell _{p}$ norm for $1\le p\le \infty$.

The Remote Set Problem [13] is defined and depends on two parameters $d, \gamma$ to be minimized, where d is the size of the output set $\varvec{S}$ by the algorithm for $RSP$ and $\gamma \ge 1$ is the remoteness parameter for which $\varvec{S}$ contains a point whose distance from $\varvec{\mathcal {L}}$ is at least $1/\gamma \cdot \rho ^{(p)}(\varvec{\mathcal {L}})$. Here, we give the definition for $V-RSP$ which only depends on remoteness parameter $\gamma$:

• $\gamma \le 1$ is a parameter such that the algorithm finds a set containing a point whose distance from $\varvec{\mathcal {L}}$ is at least $\gamma \cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ for the input lattice $\varvec{\mathcal {L}}$ and $\gamma$.

• the size of the output set $\varvec{S}$ by the algorithm can be represented by parameter $\gamma$: $|\varvec{S}|\le O(n/(\alpha \gamma )\cdot M^{\alpha \gamma })$, where $\alpha =nM/(M-1)$ and $M\ge 2$ is an integer.

Our definition for $V-RSP$ only depends on the parameter $\gamma$. The size of the output set by the algorithm for $V-RSP$ is a function of $\gamma$. Therefore, we establish relationships between the size of the output set $\varvec{S}$ and the remoteness parameter $\gamma$. The algorithm for $RSP$ in [13] is also applied to solve $V-RSP$ (see Algorithm 1). The algorithm for $V-RSP$ outputs the set $\varvec{S}$ of vectors as a linear combinations of the basis vectors with all coefficients in $\{0,1/M,\ldots ,1-1/M\}$ where $M\ge 2$ by partitioning the n basis vectors into n / k sets of size $k=\lfloor (nM/c(M-1))\cdot \gamma \rfloor \ge 1$. We show that the deterministic algorithm that on input rank n lattice $\varvec{\mathcal {L}}$ and $\gamma \le 1$ outputs a set $\varvec{S}$ of size $|\varvec{S}|\le O(n/k\cdot M^{k})$ containing at least one points which is $(1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ far from $\varvec{\mathcal {L}}$. Moreover, we show that the complexity classes that $V-RSP$ belong to with the change of parameter $\gamma$. Using the triangle inequality of norm, the analysis for $V-RSP$ can be adapted to any $\ell _{p}$ norm for $1\le p\le \infty$. In the analysis of the algorithm for $V-RSP$, we use Hölder’s Inequality to obtain that the output set containing a point has $\ell _{2}$ distance from a lattice compared with the covering radius in any $\ell _{p}$ norm for $1\le p\le \infty$. We also prove that the relationships between the output set containing a point has $\ell _{2}$ distance from a lattice and $\rho ^{(p)}(\varvec{\mathcal {L}})$ for $1\le p\le \infty$. For $p=\infty$, we do not rely on Komlós Conjecture which is essential in [13]. We also obtain that the relationships between $\ell _{p}$ distance for $1\le p\le \infty$ and $\rho ^{(2)}(\varvec{\mathcal {L}})$.

Relation to Haviv’s RSP. This paper is inspired by Haviv’s, but differs from it in most of details. The definition for $RSP$ in [13] depends on two parameters d, $\gamma \ge 1$ to be minimized, where d is the size of the set constructed and $\gamma$ is the remoteness parameter. By the analysis the algorithm for $RSP$, Haviv showed that a deterministic time algorithm for $RSP$ that on full-rank lattice $\varvec{\mathcal {L}}$ outputs a set $\varvec{S}$ of points, at least one of which is $O(\sqrt{k/n})\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ in any $\ell _{p}$ norm for $2\le p\le \infty$. Hence, the distance from the lattice of at least one of the points in $\varvec{S}$ approximates the covering radius to within a factor of $O(\sqrt{k/n})$. Haviv also showed a polynomial time deterministic algorithm outputs a set of points, at least one of which is $\sqrt{\log n/n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ far from $\varvec{\mathcal {L}}$ for $2\le p\le \infty$. The proof techniques in [13] involved a theorem on balancing vectors [5] and six standard deviations theorem [19] of Spencer from Banach space theory, and specially depended on Komlós Conjecture for $\ell _{\infty }$ norm. All the analysis of Haviv’s algorithm for $RSP$ in [13] is hold in any $\ell _{p}$ norm for $2\le p\le \infty$.

Our definition for $V-RSP$ only depends on parameter $\gamma \le 1$, the size of the set is bounded by $\gamma$ and can not minimize arbitrarily. We prove that the output of the deterministic time algorithm for $V-RSP$ contains a point in $\varvec{S}$ whose distance from lattice $\varvec{\mathcal {L}}$ is at least $O(k/n)\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ in any $\ell _{p}$ norm for $1\le p\le \infty$. This implies that the distance of a point in $\varvec{S}$ from the lattice approximates the covering radius to within a factor of O(k / n). Moreover, when we choose $k=\lfloor M/(M-1)\cdot \sqrt{n\cdot \log _{M} n}\rfloor$, we also obtain that the set S containing a point which is $\sqrt{\log _{M} n/n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ far from $\varvec{\mathcal {L}}$ for $1\le p\le \infty$ in a deterministic time. The approximation factor is similar to Haviv’s $\sqrt{\log n/n}$. We also analyze the complexity of $V-RSP$. The proof techniques for $V-RSP$ only use some elementary inequalities involving triangle inequality of norm and Hölder’s Inequality. And our results for $V-RSP$ are adapted to any $\ell _{p}$ norm for $1\le p\le \infty$.

Organization. The rest of the paper is organized as follows. In Sect. 2 we introduce basic notations about lattices and some important inequalities that we need in the paper. In Sect. 3 we propose the variant of Remote Set Problem ($V-RSP$) and analyze $V-RSP$.

2 Preliminaries

Let $\mathbb {R}^{m}$ be a m-dimensional Euclidean space. A norm $\Vert \cdot \Vert$ is a positive real-valued function on $\mathbb {R}^{m}$ that satisfies the triangle inequality, i.e., a function $\Vert \cdot \Vert :\mathbb {R}^{m}\longrightarrow \mathbb {R}$ such that

• $\Vert \varvec{x}\Vert \ge 0$ with equality only if $\varvec{x}=\varvec{0}$.

• $\Vert k\varvec{x}\Vert =|k|\Vert \varvec{x}\Vert$.

• $\Vert \varvec{x}+\varvec{y}\Vert \le \Vert \varvec{x}\Vert +\Vert \varvec{y}\Vert$.

for all $\varvec{x}, \varvec{y}\in \mathbb {R}^{m}$ and $k\in \mathbb {R}$. For $1\le p<\infty$, the $\ell _{p}$ norm of a vector $\varvec{x}=(x_{1},x_{2},\ldots ,x_{m})\in \mathbb {R}^{m}$ is defined as $\Vert \varvec{x}\Vert _{p}=(\sum _{i=1}^{m}|x_{i}|^{p})^{1/p}$ and for $p=\infty$ the $\ell _{\infty }$ norm is defined as $\Vert \varvec{x}\Vert _{\infty }=\max \limits _{1\le i\le m}|x_{i}|$. The $\ell _{p}$ distance between two vector $\varvec{x}, \varvec{y}\in \mathbb {R}^{m}$ is defined as $dist_{p}(\varvec{x},\varvec{y})=\Vert \varvec{x}-\varvec{y}\Vert _{p}$. For any vector $\varvec{x}\in \mathbb {R}^{m}$ and any set $\varvec{S}\subseteq \mathbb {R}^{m}$, the $\ell _{p}$ distance from $\varvec{x}$ to $\varvec{S}$ is $dist_{p}(\varvec{x},\varvec{S})=\min \limits _{\varvec{y}\in \varvec{S}}dist_{p}(\varvec{x},\varvec{y})$.

A lattice $\varvec{\mathcal {L}}$ is the set of all linear combinations that generated by n linearly independent vectors $\varvec{b}_{1},\ldots ,\varvec{b}_{n}$ in $\mathbb {R}^{m}$($m\ge n$), that is

$$\varvec{\mathcal {L}}=\{\sum _{i=1}^{n}x_{i}\varvec{b}_{i}|x_{i}\in \mathbb {Z},1\le i\le n\}.$$

The integer n is the rank of the lattice, m is the dimension of the lattice. The sequence of linear independent vectors $\varvec{b}_{1},\ldots ,\varvec{b}_{n}\in \mathbb {R}^{m}$ is called a basis of the lattice. We represent $\varvec{b}_{1},\ldots ,\varvec{b}_{n}$ by the matrix $\varvec{B}$ of m rows and n columns, that is, $\varvec{B}=[\varvec{b}_{1},\ldots ,\varvec{b}_{n}]\in \mathbb {R}^{m\times n}$. The lattice $\varvec{\mathcal {L}}$ generated by a basis $\varvec{B}$ is denoted by $\varvec{\mathcal {L}}=\varvec{\mathcal {L}}(\varvec{B})=\{\varvec{B}\varvec{x}:\varvec{x}\in \mathbb {Z}^{n}\}$.

In the following, we consider the covering radius which is an important parameter associated with lattices.

Definition 1

(Covering Radius). The covering radius of $\varvec{\mathcal {L}}$, denoted $\rho (\varvec{\mathcal {L}})$, is defined as the smallest radius $\rho$ such that the (closed) spheres of radius $\rho$ centered at all lattice points cover the entire space, i.e., any point in span($\varvec{\mathcal {L}}$) is within distance $\rho$ from the lattice.

Formally, the covering radius $\rho ^{(p)}(\varvec{\mathcal {L}})$ is defined as the maximum distance $dist_{p}(\varvec{x},\varvec{\mathcal {L}})$:

$$\rho ^{(p)}(\varvec{\mathcal {L}})=\max \limits _{\varvec{x}\in span(\varvec{\mathcal {L}})}{dist_{p}(\varvec{x},\varvec{\mathcal {L}})},$$

where $\varvec{x}$ ranges over the linear span of $\mathcal {L}$.

There exists a set of all the vector as a linear combinations of the basis vectors with all coefficients in $\{0,1/M,\ldots ,1-1/M\}$. The following lemma shows that at least one of the points in the set is quite far from the lattice.

Lemma 1

[10]. For every $1\le p\le \infty$, any basis $\varvec{B}$ and an integer $M>0$, there exists a point

$$\varvec{v}=a_{1}\varvec{b}_{1}+\cdots +a_{n}\varvec{b}_{n}$$

such that $a_{i}\in \{0,1/M,\ldots ,1-1/M\}$ for all i, and $dist_{p}(\varvec{v},\varvec{\mathcal {L}})\ge (1-1/M)\cdot \rho ^{(p)}(\varvec{\mathcal {L}}).$

The definition of the variant of Remote Set Problem ($V-RSP$) for any $1\le p\le \infty$ and $\gamma \le 1$ is in the following.

Definition 2

( $V-RSP _{\gamma }^{(p)}$ ). For an integer $M\ge 2$, given a lattice basis $\varvec{B}\in \mathbb {Q}^{m\times n}$ and $\gamma \le 1$, the variant of Remote Set Problem is to find a set $\varvec{S}\subseteq span(\varvec{\mathcal {L}})$ of size $|\varvec{S}|\le O(n/(\alpha \gamma )\cdot M^{\alpha \gamma })$ such that S contains a point $\varvec{v}$ satisfying

$$dist_{p}(\varvec{v},\varvec{\mathcal {L}})\ge \gamma \cdot \rho ^{(p)}(\varvec{\mathcal {L}})$$

where $\alpha =nM/(M-1).$

The following inequalities are essential in this paper.

Lemma 2

(Equivalent Norms [9]). Let $\Vert \cdot \Vert _{\alpha }$ and $\Vert \cdot \Vert _{\beta }$ be two different norms on the same vector space V. There exists positive constants t, T such that

$$t\Vert \varvec{x}\Vert _{\alpha }\le \Vert \varvec{x}\Vert _{\beta }\le T\Vert \varvec{x}\Vert _{\alpha }$$

for any vector $\varvec{x}\in V$.

Theorem 1

(Hölder’s Inequality [9]). Fix an arbitrary norm $\Vert \cdot \Vert$ on $\mathbb {R}^{m}$, for any vector $\varvec{x}\in \mathbb {R}^{m}$, we have the following inequalities:

• for any $1\le p\le 2$, $\Vert \varvec{x}\Vert _{2}\le \Vert \varvec{x}\Vert _{p}\le m^{1/p-1/2}\Vert \varvec{x}\Vert _{2}$,

• for any $2< p<\infty$, $m^{1/p-1/2}\Vert \varvec{x}\Vert _{2}\le \Vert \varvec{x}\Vert _{p}\le \Vert \varvec{x}\Vert _{2}$,

• for $p=\infty$, $\frac{1}{\sqrt{m}}\Vert \varvec{x}\Vert _{2}\le \Vert \varvec{x}\Vert _{\infty }\le \Vert \varvec{x}\Vert _{2}$.

3 The Variant of Remote Set Problem

3.1 Algorithm for the Variant of Remote Set Problem

In this section, based on Definition 2, we use triangle inequality to analyze the algorithm for $V-RSP$ which applies to any $\ell _{p}$ norm for $1\le p\le \infty$.

Theorem 2

For an integer $M\ge 2$, for every $1\le p\le \infty$ and every $k=k(n,\gamma )=\lfloor \frac{nM}{c(M-1)}\gamma \rfloor \ge 1$, there exists a deterministic $M^{k}\cdot b^{O(1)}$ time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice basis $\varvec{B}\in \mathbb {Q}^{m\times n}$ and $\gamma \le 1$, outputs a set $\varvec{S}$ of size $|\varvec{S}|=O(n/k\cdot M^{k})= O(n/(\alpha \gamma )\cdot M^{\alpha \gamma })$ containing a point which is quite far from a lattice, where $\alpha =nM/(M-1)$, n denotes lattice rank, m denotes lattice dimension, b is the input size, c is a constant.

Proof

Our proof is similar to [13], but our technique is different since we only use the triangle inequality of norm. We will give full proof for completeness here.

Assume that $k=k(n,\gamma )$ divides n. First, we partition the lattice basis $\varvec{B}=(\varvec{b}_{1},\varvec{b}_{2},\ldots ,\varvec{b}_{n})$ into n / k sets of size k each, i.e., $\varvec{B}=(\varvec{B}_{1},\varvec{B}_{2},\ldots ,\varvec{B}_{n/k})$. Then the algorithm outputs a set $\varvec{S}$ containing $n/k\cdot M^{k}$ vectors in span($\varvec{B}$) that are linear combinations of vectors in $\varvec{B}_{i}$ with coefficients in $\{0,1/M,\ldots ,1-1/M\}$. These vectors must be in some $\varvec{S}_{i},i=1,2,\ldots ,n/k$.

For every $1\le i\le n/k$, $j=1,2,\ldots ,k,$

$$\varvec{S}_{i}=\{v|v=a_{1}\varvec{b}_{(i-1)k+1}+a_{2}\varvec{b}_{(i-1)k+2}+\cdots +a_{k}\varvec{b}_{ik} \}$$

where $a_{j}\in \{0,1/M,\ldots ,1-1/M\}$. The algorithm outputs $\varvec{S}=\bigcup _{i=1}^{n/k}\varvec{S}_{i}$. Hence, we have $|\varvec{S}|\le n/k\cdot M^{k}$ and obtain $\varvec{S}$ in time $M^{k}\cdot b^{O(1)}$, where b is the input size.

For $1\le p\le \infty$, we claim that there exists a vector $\varvec{w}$ in $\varvec{S}$ such that $\ell _{p}$ distance from $\varvec{\mathcal {L}}(\varvec{B})$ is at least $(1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))$, i.e., $dist_{p}(w,\varvec{\mathcal {L}}(\varvec{B}))\ge (1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))$. Assume for contradiction that for every vector $\varvec{v}$ in $\varvec{S}$ there exists a lattice vector $\varvec{y}$ such that

$$dist_{p}(\varvec{v},\varvec{y})<(1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B})).$$

By Lemma 1, there exists a point $\varvec{v}=a_{1}\varvec{b}_{1}+a_{2}\varvec{b}_{2}+\cdots +a_{n}\varvec{b}_{n}$ such that $a_{i}\in \{0,1/M,\ldots ,1-1/M\}$ for all i and $dist_{p}(\varvec{v},\varvec{\mathcal {L}}(\varvec{B}))\ge (1-1/M)\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))$.

Let

$$\varvec{v}=\varvec{v}_{1}+\varvec{v}_{2}+\cdots +\varvec{v}_{n/k}$$

where $\varvec{v}_{i}=a_{(i-1)k+1}\varvec{b}_{(i-1)k+1}+a_{(i-1)k+2}\varvec{b}_{(i-1)k+2}+\cdots +a_{ik}\varvec{b}_{ik}$, $a_{j}\in \{0,1/M,\ldots ,1-1/M\}$ for $j=(i-1)k+1,\ldots ,ik$, $1\le i\le n/k$.

Clearly, $\varvec{v}_{i}\in \varvec{S}_{i}\subseteq \varvec{S}$, by assumption that there exists a lattice vector $\varvec{y}_{i}\in \varvec{\mathcal {L}}(\varvec{B})$ such that

$$dist_{p}(\varvec{v}_{i},\varvec{y}_{i})=\Vert \varvec{v}_{i}-\varvec{y}_{i}\Vert _{p}<(1-\frac{1}{M})\cdot \frac{k}{n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B})).$$

For every $1\le i\le n/k$, let $\varvec{\beta }_{i}=\varvec{v}_{i}-\varvec{y}_{i}$. Using the triangle inequality, we have

$$\begin{aligned} \Vert \sum _{i=1}^{n/k}\varvec{\beta }_{i}\Vert _{p}\le & {} \Vert \varvec{\beta }_{1}\Vert _{p}+\Vert \varvec{\beta }_{2}\Vert _{p}+\cdots +\Vert \varvec{\beta }_{n/k}\Vert _{p} \\< & {} (1-\frac{1}{M})\cdot \frac{n}{k}\cdot \frac{k}{n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))\\= & {} (1-\frac{1}{M})\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B})). \end{aligned}$$

Since

$$\varvec{v}-\sum _{i=1}^{n/k}\varvec{\beta }_{i}=\sum _{i=1}^{n/k}\varvec{v}_{i}-\sum _{i=1}^{n/k}\varvec{\beta }_{i}=\sum _{i=1}^{n/k}\varvec{y}_{i} \in \varvec{\mathcal {L}}(\varvec{B}),$$

we have

$$\begin{aligned} dist_{p}(\varvec{v},\varvec{\mathcal {L}}(\varvec{B}))= & {} dist_{p}(\sum _{i=1}^{n/k}\varvec{\beta }_{i},\varvec{\mathcal {L}}(\varvec{B})) \\\le & {} \Vert \sum _{i=1}^{n/k}\varvec{\beta }_{i}\Vert _{p}\\< & {} (1-\frac{1}{M})\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B})). \end{aligned}$$

This contradicts the choice of $\varvec{v}$. So, there exists a vector in $\varvec{S}$ whose $\ell _{p}$ distance from $\varvec{\mathcal {L}}(\varvec{B})$ is quite far.

Using the triangle inequality, the algorithm for $V-RSP$ is also holding in any $\ell _{p}$ norm for $1\le p\le \infty$ and solves the case of $1\le p<2$. When $M=2$, we can obtain a similar result to Haviv (see [13], Theorem 3.1), though our approximation factor is a little weaker. However, our techniques are simpler.

By choosing $k=\lfloor cM/(M-1)\cdot \sqrt{n\log _{M}n}\rfloor$, where c is a constant and n is the lattice rank, we will derive that the output of our algorithm contains a point whose distance from lattice $\varvec{\mathcal {L}}$ is at least $\sqrt{\log _{M}n/n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$. This approximation factor is similar to Haviv’s. We will describe in the following.

Corollary 1

For an integer $M\ge 2$, for every $1\le p\le \infty$ and $k=\lfloor cM/(M-1)\cdot \sqrt{n\log _{M}n}\rfloor$, there exists a deterministic time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice $\varvec{B}\in \mathbb {Q}^{m\times n}$ and $\gamma \le 1$, outputs a set containing a point which is $\sqrt{\log _{M}n/n}\cdot \rho ^{(p)}(\varvec{\mathcal {L}})$ far from lattice $\varvec{\mathcal {L}}$, where n denotes lattice rank and c is a constant.

3.2 The Complexity Classes for V-RSP

We will analyze the complexity classes for $V-RSP ^{(p)}_{\gamma }$ with the change of parameter $\gamma$, as stated in the following.

1.   For every $1\le p\le \infty$ and $0\le \epsilon \le 1$, for $\frac{1}{n}(1-\frac{1}{M})\le \gamma \le \frac{\log _{M}^{\epsilon }n}{n}(1-\frac{1}{M})$, there exists a deterministic polynomial time algorithm for $V-RSP ^{(p)}_{\gamma }$, and $V-RSP ^{(p)}_{\gamma }$ lies in Class P.

2.   For every $1\le p\le \infty$ and $\epsilon >1$, for $\frac{\log _{M}n}{n}(1-\frac{1}{M})\le \gamma \le \frac{\log _{M}^{\epsilon }n}{n}(1-\frac{1}{M})$, there exists a deterministic (single) exponential time algorithm for $V-RSP ^{(p)}_{\gamma }$.

3.3 An Additional Property of V-RSP

By the Theorem 2, we show that the algorithm for $V-RSP$ can find a set of points containing a point which is far from the lattice. We use the Hölder’s Inequality in Theorem 1 to study the relationships between the $\ell _{2}$ distance from a point of the output set to a lattice $\varvec{\mathcal {L}}$ and the covering radius ($\rho ^{(p)}(\varvec{\mathcal {L}})$) of the lattice $\varvec{\mathcal {L}}$ for every $1\le p\le \infty$. The case of $1\le p<2$ is not mentioned in [13]. Specially, when $p=\infty$, we do not depend on Komlós Conjecture. Similar to [13], the following theorems are based on algorithm presented in the proof of Theorem 2.

Theorem 3

For an integer $M\ge 2$, for every $1\le p\le 2$ and every $k=k(n,\gamma )=\lfloor \frac{nM}{c(M-1)}\gamma \rfloor \ge 1$, there exists a deterministic $M^{k}\cdot b^{O(1)}$ time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice basis $\varvec{B}\in \mathbb {R}^{m}$ and $\gamma \le 1$ outputs a set $\varvec{S}$ of size $|\varvec{S}|=O(n/k\cdot M^{k})=O(n/(\alpha \gamma )\cdot M^{\alpha \gamma })$ containing a point whose $\ell _{2}$ distance from $\varvec{\mathcal {L}}$ is at least $1/m^{1/p-1/2} \cdot (1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))$, where $\alpha =nM/(M-1)$, m denotes lattice dimension, b is the input size, c is a constant. For a special case of full-rank lattice($m=n$), one of the points whose $\ell _{2}$ distance is at least $k/n^{1/p+1/2} \cdot (1-1/M)\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B})).$

Theorem 4

For an integer $M\ge 2$, for every $2< p\le \infty$ and every $k=k(n,\gamma )=\lfloor \frac{nM}{c(M-1)}\gamma \rfloor \ge 1$, there exists a deterministic $M^{k}\cdot b^{O(1)}$ time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice $\varvec{B}\in \mathbb {R}^{m}$ and $\gamma \le 1$, outputs a set $\varvec{S}$ of size $|\varvec{S}|=O(n/k\cdot M^{k})=O(n/(\alpha \gamma )\cdot M^{\alpha \gamma })$ containing a point whose $\ell _{2}$ distance from $\varvec{\mathcal {L}}$ is at least $(1-1/M)\cdot k/n\cdot \rho ^{(p)}(\varvec{\mathcal {L}}(\varvec{B}))$, where $\alpha =nM/(M-1)$, m denotes lattice dimension, b is the input size, c is a constant.

In the following, we study the relationships between the $\ell _{p}$($1\le p\le \infty$) distance from a point of the output set to a lattice $\varvec{\mathcal {L}}$ and the covering radius ($\rho ^{(2)}(\varvec{\mathcal {L}})$) of the lattice $\varvec{\mathcal {L}}$.

Corollary 2

For an integer $M\ge 2$, for every $1\le p\le 2$ and every $k=k(n,\gamma )=\lfloor \frac{nM}{c(M-1)}\gamma \rfloor \ge 1$, there exists a deterministic $M^{k}\cdot b^{O(1)}$ time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice $\varvec{B}\in \mathbb {R}^{m}$ and $\gamma \le 1$ outputs a set $\varvec{S}$ of size $|\varvec{S}|=O(n/k\cdot M^{k})$ containing a point whose $\ell _{p}$ distance from $\varvec{\mathcal {L}}$ is at least $(1-1/M)\cdot k/n\cdot \rho ^{(2)}(\varvec{\mathcal {L}}(\varvec{B}))$. For every $2< p<\infty$, one of points whose $\ell _{p}$ distance is at least $1/m^{1/p-1/2} \cdot (1-1/M)\cdot k/n\cdot \rho ^{(2)}(\varvec{\mathcal {L}}(\varvec{B}))$. For a the full-rank lattice $(m=n)$, one of the points whose $\ell _{p}$ distance is at least $k/n^{1/p+1/2} \cdot (1-1/M)\cdot \rho ^{(2)}(\varvec{\mathcal {L}}(\varvec{B}))$, where m denotes lattice dimension, b is the input size, c is a constant.

Corollary 3

For an integer $M\ge 2$, for every $p=\infty$ and every $k=k(n,\gamma )=\lfloor \frac{nM}{c(M-1)}\gamma \rfloor \ge 1$, there exists a deterministic $M^{k}\cdot b^{O(1)}$ time algorithm for $V-RSP _{\gamma }^{(p)}$ that on input a lattice $\varvec{B}\in \mathbb {R}^{m}$ and $\gamma \le 1$ outputs a set $\varvec{S}$ of size $|\varvec{S}|=O(n/k\cdot M^{k})$ containing a point whose $\ell _{p}$ distance from $\varvec{\mathcal {L}}$ is at least $1/\sqrt{m} \cdot (1-1/M)\cdot k/n\cdot \rho ^{(2)}(\varvec{\mathcal {L}}(\varvec{B}))$, where m denotes lattice dimension, b is the input size, c is a constant.

4 Conclusion

In our paper, we propose the variant of Remote Set Problem ($V-RSP$) which only relies on the parameter $\gamma \le 1$. From the algorithm for $RSP$, we knew that the distance from the lattice of at least one of the point in the set $\varvec{S}$ approximates the covering radius to within a factor of $O(\sqrt{k/n})$ in $\ell _{p}$ norm for $2\le p\le \infty$. However, using some elementary tools, we obtain that the approximation is O(k / n) in the algorithm for $V-RSP$ in $\ell _{p}$ norm for $1\le p\le \infty$. This introduces a $O(\sqrt{k/n})$ loss in the approximation factors. We also can get the same approximation factors at the cost of more time in the algorithm for $V-RSP$. Hence, there is an interesting problem to reduce the gap between $RSP$ and $V-RSP$.