Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The extraction of multiple models from noisy or outlier-contaminated data – a.k.a. Multiple Structure Recovery (MSR) – is an important and challenging problem that emerges in many Computer Vision applications [7, 10, 31]. With respect to single-model estimation in presence of noise and outliers, MRS aims at facing the so called pseudo-outliers (i.e. “outliers to the structure of interest but inliers to a different structure” [27]), which push robust estimation to its limit. If, in addition, the number of structures is not known in advance, MSR turns into a thorny model-selection problem, as one have to pick, among all the possible interpretations of the data, the most appropriate one.

In the literature, the problem of MSR has been successfully tackled by leveraging on clustering techniques [13, 18, 19, 25]. Generally, the data matrix to analyze reports the points to cluster on one dimension and the features/descriptors on the other dimension [1]. Clustering approaches group the rows (or the columns) of a given data matrix on the basis of a similarity criterion. For example in these recent approaches J-linkage[30], T-linkage [18] and RPA [19]. The feature vector used to represent data is derived form the preferences expressed by the data points for a pool of tentative structures obtained by random sampling. Hence cluster analysis is performed via either agglomerative or partitional methods where distances measure the (dis)agreement between preferences.

Although it has been shown that clustering provides good solution to the MSR problem, there are situations where the performances of clustering can be highly compromised by data matrix structure (e.g. noisy data matrices; or rows behaving similarly only in a small portion of the data matrix). Retrieving information in scenarios where clustering struggles can be done through a recent class of approaches called biclustering.

Fig. 1.
figure 1

Example of overlapping biclusters on Multiple Structure Recovery. In this case the possible biclusters are the: \(b_1\)) the points lying on \(m_1\), \(b_2\)) the points lying on \(m_2\) and \(b_3\)) the points lying on the intersections.

Full size image

With the term bi-clustering we refer to a specific category of algorithms performing clustering on both rows and columns of a given data matrix [17]. The goal of biclustering is to isolate sub-matrices where the rows present a “coherent behavior” in a restricted columns subset, and vice-versa. Compared with clustering, biclustering exploits local information to retrieve structures that cannot be found performing analysis on whole rows or columns. The problem of biclustering (also known as co-clustering, and strongly related to subspace clustering) is gaining increasing attention in the Pattern Recognition community, with many papers being published in recent years (e.g. [4, 8, 11, 22]). Even if it was originally proposed in biological scenarios (i.e. analysis of gene expression microarray datasets [2, 17, 20]), biclustering has been widely adopted in many other contexts ranging from market segmentation to data mining [6, 14, 21].

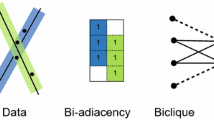
This paper is positioned exactly in this context, investigating the performance of biclustering on MSR. The main advantage of using biclustering on MSR is that biclustering can isolate portions of the data matrix where a subset of points share similar attitudes in a subset of models. Compared to clustering, biclustering retrieves additional information on which models better describes a particular subset of points. Moreover, biclustering provides better understanding of the data since different biclusters can overlap (on rows, columns or both). This means that a certain point can belong to different biclusters and hence it can be characterized by distinct subsets of models (see Fig. 1 for an example). Thus biclustering approaches can easily deal with intersections, which is a known problematic situation when using clustering algorithms [28].

To the best of our knowledge there exists only a preliminar work applying biclustering techniques to MSR [28]. In [28] authors show that the application of biclustering techniques to MSR is promising and provides superior solution when compared with clustering. While this provides a significant contribution to the state of the art, there is large room for improvements since the method adopted by the authors has some limitations (i.e. it works with sparse binary matrices and it needs some pre-processing/post-processing operations to retrieve the final solutions).

In this paper we investigate the use of a recent probabilistic biclustering approach, namely Factor Analysis for BIcluster Acquisition (FABIA) [12] for MSR. We choose this algorithm because it has been shown to perform better than the state of the art in the Microarray Gene Expression analysis, a widely exploited scenario to test biclustering algorithms [12, 17].

We evaluate the performances of probabilistic biclustering on a real benchmark dataset (Adelaide dataset) and we compare against the recent clustering algorithms adopted for MSR. Results confirm that biclustering favorably compares with the state-of-the-art.

The reminder of the paper is organized as follows: Sect. 2 provides a brief review of MSR and the clustering methods we compare to. Section 3 formalizes the biclustering problem and the algorithm we adopt. Section 4 presents and discusses the experimental evaluation. Finally, some concluding remarks are presented in Sect. 5

2 Background and Related Work

This section provides background knowledge about the proposed framework. It formalizes the MSR problem and the clustering approaches currently adopted.

2.1 Multiple Structure Recovery

MSR aims at retrieving parametric models from unstructured data in order to organize and aggregate visual content in significant higher-level geometric structures. This task is commonly found in many Computer Vision applications, a typical example being 3D reconstruction, where MSR is employed either to estimate multiple rigid moving objects (to initialize multibody Structure from Motion [7, 23]), or to produce intermediate geometric interpretations of reconstructed 3D point cloud [10, 31]. Other instances include face clustering, body-pose estimation and video motion segmentation. In all these scenarios the information of interest can be extracted from the observed data and aggregated in suitable structures by estimating some underlying geometric models, e.g. planar patches, homographies, fundamental matrices or linear subspaces.

More formally, to set a general context, let \(\mu \) be a model e.g. lines, subspace, homography, fundamental matrices or other geometric primitives and \(X = \{x_1,\ldots ,x_n\}\) be a finite set of n points, possibly corrupted by noise and outlier. The problem of MSR consists in extracting k instances of \(\mu \) termed structures from the data, defining, at the same time, subsets \(C_i \subset X, i = 1,\ldots \), such that all points described by the i-th structures are aggregated in \(C_i\). Often the models considered are parametric, i.e. the structures can be represented as vectors in a proper parameter space.

2.2 Clustering

The extensive landscape of approaches aimed at MSR can be broadly categorized along two mutually orthogonal strategies, namely consensus analysis and preference analysis. Focusing on preference analysis, these methods reverse the role of data and models: rather than considering models and examining which points match them, the residuals of individual data points are taken into account [3, 29, 32]. This information is exploited to shift the MSR problem from the ambient space where data lives to a conceptual [24] one where it is addressed via cluster analysis techniques.

T-Linkage [18] and RPA [19] can be ascribed to these clustering-based methods as they share the same first-represent-then-clusterize approach. Both the algorithms represent data points in a m-dimensional unitary cube as vectors whose components collect the preferences granted to a set of m hypotheses structures instantiated by drawing at random m minimal sample sets – the minimum-sized set of data points necessary to estimate a structure. Preferences are expressed with a soft vote in [0, 1] according to the continuum of residuals in two different fashions. As regards T-linkage, a voting function characterized by an hard cutoff is employed. RPA, instead, exploits the Cauchy weighting function (of the type employed in M-estimators) that has an infinite rejection point mitigating the sensitivity of the inlier threshold.

The rationale beyond both these representations is that the agreement between the preferences of two points in this conceptual space reveals the multiple structures hidden in the data: points sharing the same preferences are likely to belong to the same structures.

T-Linkage captures this notion through the Tanimoto distance, which in turn is used to segment the data via a tailored version of average linkage that succeeds in detecting automatically the number of models. If rogue points contaminate the data, outlier structures need to be pruned via ad hoc-post processing techniques.

RPA, on the contrary, requires the number of desired structures as input but inherently caters for gross contamination. At first a kernelized version of the Tanimoto distances is feed to Robust Principal Analysis to remove outlying preferences. Then Symmetric Non Negative Factorization [15] is performed on the low rank part of the kernel to segment the data. Hence, the attained partition is refined in a MSAC framework. More precisely, the consensus of the sampled hypotheses are scrutinized and the structures that, within each segment, support more points are retained as solutions.

While T-linkage can be considered as a pure preference method, RPA attempts to combine also the consensus-side of the MSR problem. However it does not fully reap the benefit of working with both the dimensions of the problem, as biclustering does, for preference and consensus are considered only sequentially.

All these methods can be regarded as processing the Preference Matrix, where each entry (i, j) represents the vote granted by the i-th point to the j-th tentative structures. Rows of that matrix provides the representation of points that are used to derive the affinity matrices for clustering. Column of that matrix are the consensus set of a model hypothesis.

An example where clustering struggles is provided in Fig. 2, which describes a simple MSR problem: to group similar points on the basis of their behavior with respect to the proposed models we should perform clustering on the Preference Matrix P which describes the relationship between the points \(\{x_1, x_2, x_3, x_4\}\) and the models \(\{m_1, \cdots , m_{13}\}\). Assume we perform clustering adopting the Hamming distance (i.e. number of different bits): since the distance between the \(x_3\) and the \(x_4\) is smaller than the distance between \(x_3\) and \(x_2\), clustering would assign the third and the fourth point to the same group. However looking at the problem diagram it is clear that points \(x_1, x_2\) and \(x_3\) should belong to the same cluster. This information can be retrieved performing a simultaneous clustering of both rows and columns of the Preference Matrix, isolating a subset of models \((m_1, m_2\) and \(m_3)\) where the points \({x_1, x_2, x_3}\) share a similar behavior (shaded area in Fig. 2). This is exactly what biclustering techniques do.

Next section provides a more formal definition of the biclustering problem, focusing on the approach adopted to analyze the Preference Matrix (FABIA [12]).

Fig. 2.
figure 2

Shortfalls of clustering on MRS.

Full size image

3 Biclustering

As mentioned in Sects. 1 and 2.2 the goal of biclustering applied to MSR is the simultaneous clustering of points and structures/models of a given Preference Matrix, merging the well known concepts of consensus analysis and preference analysis. Due to the similarity of RPA (where the kernelized matrix is factorized in order to obtain point clusters) we present biclustering from a sparse low-rank matrix factorization perspective, also the most suitable to understand the insights behind the FABIA algorithm [12].

We denote as \(D \in \mathbb {R}^{n\times m}\) the given data matrix, and let \(R = \{1,\dots ,n\}\) and \(C = \{1,\dots ,m\}\) be the set of row and column indices. We adopt \(D_{TK}\), where \(T\subseteq R\) and \(K\subseteq C\), to represent the submatrix with the subset of rows in T and the subset of columns in K. Given this notation, we can define a bicluster as a submatrix \(D_{TK}\), such that the subset of rows of D with indices in T exhibits a “coherent behavior” (in some sense) across the set of columns with indices in K, and vice versa. The choice of coherence criterion defines the type of biclusters to be retrieved (for a comprehensive survey of biclustering criteria, see [8, 17, 22]).

A possible coherence criterion for a bicluster (sub-matrix) is for the corresponding entries to have a similar value, significantly different from the other entries of the matrix. For example, a data matrix containing one bicluster with rows \(T = \{1,2,3,4\}\) and columns \(K = \{1,2\}\) may look like

$$\begin{aligned} D = \begin{bmatrix} \mathbf {10}&\mathbf {10}&0&0 \\ \mathbf {10}&\mathbf {10}&0&0 \\ \mathbf {10}&\mathbf {10}&0&0 \\ \mathbf {10}&\mathbf {10}&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ \end{bmatrix} ,\quad v = \begin{bmatrix} \mathbf 5 \\ \mathbf 5 \\ \mathbf 5 \\ \mathbf 5 \\ 0\\ 0\\ \end{bmatrix} , \quad z = \begin{bmatrix} \mathbf 2 \\ \mathbf 2 \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

From an algebraic point of view, this matrix can be represented by the outer product \(D = v z^T\) of the sparse vectors v and z. We call these vectors prototypes (for v) and factors (for z). Generalizing to k biclusters, we can formulate the biclustering problem as the decomposition of the given data matrix D as the sum of k outer products,

$$\begin{aligned} D = \sum _{i = 1}^{k} v_i z_i^T= VZ, \end{aligned}$$
(1)

where \(V = [v_1, \dots , v_k] \in \mathbb {R}^{n\times k}\) and \(Z = [z_1, \dots , z_k]^T \in \mathbb {R}^{k\times m}\).

The connection between biclustering and sparse low-rank matrix factorization can be highlighted by observing that the factorization of the original data matrix shows that it has rank no larger than the number of biclusters (usually much lower than the number of rows or columns). Moreover, if the size of the matrix D is much bigger than the bicluster size (as it is typically the case in many applications), the resulting prototype and factor vectors should be composed mostly by zeros (i.e., the prototypes and factors should be sparse).

3.1 FABIA

In the biclustering literature, there are several proposals of biclustering methods through matrix factorization (e.g., [16, 33]); however, to the best of our knowledge, the only probabilistic approach is FABIA.

FABIA is a generative model for biclustering based on factor analysis [12]. The model proposes to decompose the data matrix by adding noise to the strict low rank decomposition in (1),

$$\begin{aligned} D = \sum _{i = 1}^{k} v_i z_i^T + Y = VZ + Y, \end{aligned}$$
(2)

where matrix \(Y \in \mathbb {R}^{n \times m}\) accounts for random noise or perturbations, assumed to be zero-mean Gaussian with a diagonal covariance matrix. As explained above (Sect. 3) the prototypes in V and factors in Z should be sparse. To induce sparsity, FABIA uses two types of priors: (i) an independent Laplacian prior, and (ii) a prior distribution that is non-zero only in region where prototypes are sparse (for further details, see [12]). The model parameters are estimated using a variational EM algorithm [9, 12], for all the details about FABIA derivation and implementationFootnote 1, please refer to [12].

4 Experimental Evaluation

This section provides the performances comparison between some clustering methods recently applied to MSR [18, 19, 25] and the probabilistic biclustering approach presented in Sect. 3.1. The comparison with [28] was not possible since the code is not available. The workflow of the overall procedure can be sketched as follows: starting from an image (i) we generate the hypothesis and compute the Preference Matrix following the guidelines in [19]; (ii) then the probabilistic biclustering technique have been applied.

To assess the quality of the approaches we used the widely adopted Adelaide real benchmark datasetFootnote 2. Moreover we conduct a reproducibility analysis, since it is known that RPA algorithm can produce very different solutions due to the random initialization required by the Symmetric NNMF step.

4.1 Adelaide Dataset

We explored the performances of probabilistic biclustering on two type of experiments, namely motion and plane estimation. In motion segmentation experiments, we were provided with two different images of the same scene composed by several objects moving independently; the aim was to recover fundamental matrices to subsets of point matches that undergo the same motion. With respect to the plane segmentation scenario, given two uncalibrated views of a scene, the goal was to retrieve the multi-planar structures by fitting homographies to point correspondences. The AdelaideRMF dataset is composed of 38 image pairs (19 for motion segmentation and 19 for plane segmentation) with matching points contaminated by gross outliers. The ground-truth segmentations are also available. In order to assess the quality of the results, we adopted the misclassification errors, that counts the number of wrong point assignment according to the map between ground-truth labels and estimated ones that minimize the overall number of misclassified points (as in [26]). For fair comparison, the Preference Matrix fed to FABIA was generated relying on the guided sampling scheme presented in [19].

Table 1. Misclassification error (ME %) for motion segmentation (left) and planar segmentation (right). k is the number of models and % out is the percentage of outliers.
Full size table

FABIA parameters which regulate the factors/prototypes sparsity and the threshold to retrieve biclusters memberships have been varied in the range suggested by the authors in [12]. The best results on the whole Adelaide dataset (motion and plane estimation) are reported in Table 1. The performances of other methods are taken from [19]; results show that FABIA provides higher quality solutions on the motion segmentation dataset, and on average it performs better on the planar segmentation. Focusing on the motion segmentation dataset, there are only three situations where FABIA works worse than clustering approaches. A possible explanation on why FABIA struggles could be because general biclustering approaches are tested in scenarios where the number of biclusters is much higher than in MSR (i.e. \(\sim \)100 in Gene Expression analysis versus 3–7 in this dataset). To overcome this behavior we run FABIA increasing the number of biclusters to retrieve and aggregating the results on the basis of column overlap as done in [5], this leads to an improvement of the solution quality; results are reported in Table 2.

Table 2. Increasing the number of biclusters improve the results obtained by FABIA on the motion segmentation dataset.
Full size table

4.2 Reproducibility

In this section we assess the reproducibility of the two methods that better perform on the Adelaide dataset: RPA and FABIA. The goal is to demonstrate that probabilistic approaches can overcome the problem of reproducibility present in RPA. For a fair comparison we adopted the 2R3RTCRT video sequence from the Hopkins datasetFootnote 3: a dataset where both the approaches retrieve good and similar solutions.

Hopkins dataset is a motion segmentation benchmark where the input data consists in a set of features trajectories across a video taken by a moving camera, and the problem consist in recovering the different rigid-body motions contained in the dynamic scene. Motion segmentation can be seen as a subspace clustering problem under the modeling assumption of affine cameras. In fact, under the assumption of affine projection, it is simple to demonstrate that all feature trajectories associated with a single moving object lie in a linear subspace of dimension at most 4 in \(\mathbb {R}^{2F}\) (where F is the number of video frames). Feature trajectories of a dynamic scene containing k rigid motion lie in the union of k low dimensional subspace of \(\mathbb {R}^{2F}\) and segmentation can be reduced to clustering data points in a union of subspaces.

To test the reproducibility of RPA and FABIA we run the algorithms on the same Preference Matrix hundred times, and for each trial we assess the misclassification error; the results are reported in Fig. 3. The figure shows the result obtained by the approaches in each iteration and its distance from the average results. Results clearly show that while the two approaches are compatible on average, FABIA retrieves the same solution in each iteration while RPA is much less stable.

Fig. 3.
figure 3

Reproducibility. The methods have been run 100 times on the same Preference Matrix. Plots show the misclassification error in of each trials along with the distance from the mean (RPA mean = 1.93 %, FABIA mean = 1.95 %).

Full size image

5 Conclusion and Discussion

In this paper we present an alternative to clustering for the problem of Multiple Structure Recovery (MSR), namely biclustering. In general, biclustering techniques allow to retrieve superior and more accurate information than clustering approaches, characterizing each cluster of points with the subset of features that better describes them. The goal of biclustering approaches applied to MSR is isolate submatrices inside the Preference Matrix where a subset of points behave “coherently” in a subset of models/structures. We tested the recent probabilistic biclustering approach FABIA on the Adelaide benchmark dataset, proving that it favorably compares with the state of the art. Moreover we tested the reproducibility of the analyzed methods showing that FABIA is much more stable than the second competitor RPA.