1 Introduction

Spherical deconvolution [14] is widely used to analyze white matter (WM) in high angular resolution diffusion imaging (HARDI). Recently, it has been shown that, when HARDI data is available on multiple shells, parameters related to the volume fractions of gray matter (GM) and corticospinal fluid (CSF) can be added to the deconvolution model [3, 5]. An important advantage of this is increased accuracy in voxels with partial voluming between different tissue types.

We present a novel method for multi-tissue deconvolution that makes two main contributions: First, non-negativity constraints have long been recognized as an indispensible regularization in deconvolution, and are most frequently enforced at a set of discrete points on the sphere [14, 16]. In contrast, we derive a positive definiteness constraint from a higher-order tensor representation of the fiber orientation distribution function (fODF) which implies non-negativity everywhere on the sphere. It can be implemented easily using quadratic cone programming, and can be combined both with multi-tissue and traditional single-shell single-tissue deconvolution.

Second, many dMRI acquisition schemes do not use a shell structure. This includes Diffusion Spectrum Imaging [15], which uses a Cartesian grid, and some recently proposed schemes that distribute samples freely in Q-space [7, 9]. Our approach improves upon previous multi-tissue deconvolution methods, which have modeled the signal on each shell separately [3, 5], by instead estimating the tissue response as a continuous function in Q-space, using the SHORE basis functions [8]. This allows us to work with data that is not organized on shells.

In a direct comparison between our approach and a state-of-the-art alternative [5], we demonstrate that ours is more well-conditioned, more accurate at small angles, and faster.

2 Related Work

Our approach extends previous work that has used higher-order Cartesian tensors to represent fiber ODFs [6, 11, 13, 16] by the ability to handle data acquired at multiple b-values and by modeling multiple tissue types.

Our H-psd constraint is new, and stronger than the non-negativity constraints used previously when estimating higher-order diffusion tensors [1, 4], or in the non-negative spherical deconvolution (NNSD) [2] approach. In addition, in contrast to NNSD, our method can be implemented using standard convex cone optimization packages rather than requiring a custom implementation of a computationally expensive Riemannian gradient descent.

3 Fiber ODFs are H-psd Tensors

Our approach extends previous work [13], which has proposed to describe fODFs f by fully symmetric fourth order tensors:

$$\begin{aligned} f({\mathbf {v}}) = T({\mathbf {v}}) = \sum _{i,j,k,l=1}^{3} T_{ijkl} \, v_i v_j v_k v_l, \quad {\mathbf {v}} \in {\mathbb {S}}^2 \end{aligned}$$
(1)

Such fODF tensors T are obtained by deconvolution in the Spherical Harmonics basis and a subsequent change to the monomial basis, which spans the same space of functions. However, there are two important differences to standard spherical deconvolution [14]: First, the deconvolution step is constructed so that it maps the single fiber response in direction \({\mathbf {v}}\) to a symmetric rank-one tensor \({\mathbf {v}}\otimes {\mathbf {v}}\otimes {\mathbf {v}}\otimes {\mathbf {v}}\), rather than to a truncated delta peak. Second, principal fODF directions for fiber tractography are found using a low-rank approximation of the fODF tensor, rather than peaks in the fODF function.

The set of symmetric three-dimensional fourth-order tensors will be denoted by \(S_{3,4}\). The subset of positive semidefinite tensors is

$$\begin{aligned} P_{3,4} = \{ T \in S_{3,4} : T({\mathbf {v}}) \ge 0 \quad \forall {\mathbf {v}} \in {\mathbb {S}}^2 \} \, . \end{aligned}$$
(2)

As pointed out in Chap. 5 of [10], \(T \in S_{3,4}\) has an associated matrix

$$\begin{aligned} H_T = \begin{pmatrix} T_{xxxx} &{} T_{xxxy} &{} T_{xxxz} &{} T_{xxyy} &{} T_{xxyz} &{} T_{xxzz} \\ T_{xxxy} &{} T_{xxyy} &{} T_{xxyz} &{} T_{xyyy} &{} T_{xyyz} &{} T_{xyzz} \\ T_{xxxz} &{} T_{xxyz} &{} T_{xxzz} &{} T_{xyyz} &{} T_{xyzz} &{} T_{xzzz} \\ T_{xxyy} &{} T_{xyyy} &{} T_{xyyz} &{} T_{yyyy} &{} T_{yyyz} &{} T_{yyzz} \\ T_{xxyz} &{} T_{xyyz} &{} T_{xyzz} &{} T_{yyyz} &{} T_{yyzz} &{} T_{yzzz} \\ T_{xxzz} &{} T_{xyzz} &{} T_{xzzz} &{} T_{yyzz} &{} T_{yzzz} &{} T_{zzzz} \end{pmatrix} \end{aligned}$$
(3)

that represents T’s action on the six-dimensional space of symmetric products \({\mathbf {v}} \otimes {\mathbf {v}}\). We will denote the subset of tensors with a positive semidefinite matrix \(H_T\) as

$$\begin{aligned} P_H = \{T \in S_{3,4} : H_T \; {\mathrm {is \, psd}} \} \end{aligned}$$
(4)

and call these tensors H-psd.

\(P_H\) is closely related to decomposable tensors. To show this, let

$$\begin{aligned} Q_{3,4} = \{ T \in S_{3,4} : T({\mathbf {v}}) = \sum _{i=1}^k \langle \alpha _i, {\mathbf {v}} \rangle ^4 \} \end{aligned}$$
(5)
$$\begin{aligned} \varSigma _{3,4} = \{ T \in S_{3,4} : T({\mathbf {v}}) = \sum _{i=1}^k h_i^{\,2}({\mathbf {v}}) \} \end{aligned}$$
(6)

be the subsets of tensors that are sums of fourth powers and sums of squares, respectively. Due to their geometric structure, these sets are called cones. They obey

$$\begin{aligned} Q_{3,4} \subsetneq \varSigma _{3,4} \subseteq P_{3,4} \, . \end{aligned}$$
(7)

Obviously, sums of squares and sums of fourth powers are positive semidefinite. In fact, a result by Hilbert, which has been applied to enforce non-negativity of fourth-order diffusion tensors [1, 4], states that \(P_{3,4} = \varSigma _{3,4}\). In contrast, not every tensor in \(P_{3,4}\) can be written as a sum of fourth powers [10].

The dual of a cone C is defined as \( C^\star = \{ y \in C : \langle x,y \rangle \ge 0 \; \forall x \in C \} \) and, in [10], it is shown that

$$\begin{aligned} \varSigma _{3,4}^\star = P_H \quad {\mathrm {and}} \quad P_{3,4}^\star = Q_{3,4} \, . \end{aligned}$$
(8)

Combining these dualities with the dual of the result by Hilbert yields

$$\begin{aligned} Q_{3,4} = P_{3,4}^\star = \varSigma _{3,4}^\star = P_H \, , \end{aligned}$$
(9)

i.e., a tensor in \(S_{3,4}\) can be written as a sum of fourth powers or, equivalently, decomposed into symmetric rank-1 terms, if and only if it is H-psd.

For spherical deconvolution, this has the following implications: First, fODF tensors arise from a mixture of an unknown number of single-fiber compartments, each of which is represented as a symmetric rank-1 tensor. Therefore, any valid fODF tensor must be decomposable. Second, decomposability can be checked easily by positive semidefiniteness of Eq. (3) (H-psd). Third, as Eq. (7) shows, H-psd is a stronger condition than simple non-negativity, as it has been imposed previously on fODFs [2, 14], or on fourth-order diffusion tensors [1, 4].

4 Using SHORE for Multi-tissue Deconvolution

Multi-tissue deconvolution requires modelling the dMRI response of all tissue types. Previous approaches [3, 5] do so separately for each shell. To avoid dependence on a shell structure, we instead create a continuous model of functions \(f(\mathbf{q } = q \mathbf{u })\) in Q-space using the SHORE basis functions [8]

$$\begin{aligned} \phi _{lnm}(\mathbf{q }) = \Biggl [\dfrac{2(n-l)!}{\zeta ^{3/2} \varGamma (n+3/2)} \Biggr ]^{1/2} \Biggl (\dfrac{q^2}{\zeta }\Biggr )^{l/2} {\mathrm {exp}}\Biggl (\dfrac{-q^2}{2\zeta }\Biggr ) L^{l+1/2}_{n-l} \Biggl (\dfrac{q^2}{\zeta }\Biggr ) Y_l^m(\mathbf{u }) \end{aligned}$$
(10)

with the associated Laguerre polynomials \(L^\alpha _n\), the real Spherical Harmonics \(Y_l^m\) and a radial scaling factor \(\zeta \).

Let \(K(\mathbf{q }) = \sum _{ln} K_{ln} \, \phi _{ln0}(\mathbf{q })\) be the white matter single-fiber response, with \(m=0\) due to cylinder symmetry. The signal from an fODF f is then modeled by a convolution on the sphere, \(S(\mathbf{q }) \approx K \star _{{\mathbb {S}}^2} f\) [2]. For a given K and signal vector \(S_i = S(\mathbf{q }_i)\), finding the Spherical Harmonics coefficients f via deconvolution then becomes a linear least squares problem with a nonlinear constraint:

$$\begin{aligned} {\text {argmin}}_{f} \Vert M f - S \Vert ^2 \quad {\mathrm {subject\, to}} \quad f \in P_H \end{aligned}$$
(11)

with convolution matrix

$$\begin{aligned} M_{(i)(lm)} = \sum _n \frac{1}{\alpha _l} \, K_{ln} \, \phi _{lnm}(\mathbf{q }_i). \end{aligned}$$
(12)

As in [13], the \(\alpha _l\) are the Spherical Harmonics coefficients of the unit rank-1 tensor along the z-axis.

The problem is equivalent to the quadratic cone program (QCP)

$$\begin{aligned} {\text {argmin}}_{f} \frac{1}{2} \langle f, P f \rangle + \langle q, f \rangle \quad {\mathrm {subject\, to}} \quad (G f) {\mathrm {\, psd}} \end{aligned}$$
(13)

with \(P = M^T M\), \(q = -M^T S\), and a matrix G that first maps f from Spherical Harmonics to the monomial basis, and then to its \(H_T\) matrix, \(G f = H_f\). This QCP can be solved efficiently using cvxopt (cvxopt.org).

Multi-tissue support is added by concatenating individual tissue matrices

$$\begin{aligned} M = \left[ M_{\mathrm {CSF}}, M_{\mathrm {GM}}, M_{\mathrm {WM}} \right] , \quad f = \begin{bmatrix} f_{\mathrm {CSF}} \\ f_{\mathrm {GM}} \\ f_{\mathrm {WM}} \end{bmatrix} \, . \end{aligned}$$
(14)

Since CSF and GM are isotropic, \(M_{\mathrm {CSF}}\) and \(M_{\mathrm {GM}}\) are single-column matrices. In the QCP, non-negativity constraints are enforced for \(f_{\mathrm {GM}}\) and \(f_{\mathrm {CSF}}\).

5 Results

5.1 Condition and Computational Efficiency

We compared our method to the approach of Jeurissen et al. [5], using cvxopt in both cases. We used data provided by the Human Connectome Project (HCP) with 270 DWIs, 90 each at \(b\approx \{1000,2000,3000\}\) s/mm\(^2\), and a two-shell clinical data set (“clin-2-sh”) with 94 DWIs, 30 at \(b=700\) and 64 at \(b=2000\). We also show results on another clinical data set (“clin-dsi”) with 128 DWIs, acquired on a Cartesian grid with \(b_{{\mathrm {max}}}=3000\). The approach in [5] cannot be applied to this data, since it includes many different b values with few directions each.

Tissue response functions were estimated as described previously [5], based on tissue segmentation of a coregistered \(T_1\) image, and FA thresholds (\({\mathrm {FA}} > 0.7\) for white matter, \({\mathrm {FA}} < 0.2\) for CSF), except that we model the responses in the SHORE basis as described in Sect. 4.

The processing time (on a single CPU core) as well as the condition number of the matrix P in the quadratic program are listed in Table 1. The fact that we use fourth-order fODFs makes the problem much better conditioned. Our method is also significantly faster, despite the fact that we guarantee non-negativity everywhere, instead of enforcing it only at discrete points. We will now demonstrate that, when combined with tensor approximation [13], order 4 is sufficient to resolve crossings, and even more accurate at smaller angles.

Table 1. Our approach is much better conditioned than the traditional one, and requires less computation. Unlike the existing method, it is applicable also to DSI data
Full size table

5.2 Accuracy on Simulated Data

Evaluating the accuracy of our method requires data for which volume fractions and orientations of crossing fiber compartments are known. From an HCP data set, we extracted the signal from voxels believed to contain a single fiber of white matter, i.e., being within the white matter mask and having \({\mathrm {FA}}>0.7\). The fiber direction for each voxel was estimated by fitting the diffusion tensor model and finding the eigenvector to the highest eigenvalue. Every voxel of simulated data was created by randomly choosing several single fiber voxels and a voxel with \({\mathrm {FA}}<0.2\) from either the grey matter or the CSF mask, and adding their signals with random volume fractions.

For comparison, we evaluated the original method by Jeurissen et al. [5], our proposed method, as well as a hybrid, which uses our novel regularization and tensor decomposition, but models the response functions using Spherical Harmonics for each shell, rather than SHORE.

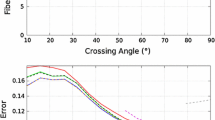
The accuracy of estimated fiber directions and volume fractions on simulated data containing two fibers can be seen in Fig. 1. They demonstrate that, for crossing angles below \(60^\circ \), order-4 tensor approximation reconstructs the fibers much more accurately than finding peaks in order-8 fODFs. The theoretical advantage of H-psd being stricter than non-negativity becomes relevant for small angles, starting around \(40^\circ \). Our simulated data includes the noise from the HCP data from which it was generated. We tried adding more noise, and observed that this increased the advantage of using the H-psd constraint.

Practically no difference is visible when replacing SHORE with Spherical Harmonics models on each shell. This demonstrates that, while SHORE is more flexible in that it does not assume a multi-shell structure, it does not decrease accuracy when data is given on shells.

Fig. 1.
figure 1

On simulated two-fiber crossings with variable amounts of GM and CSF, our method estimates fiber directions and volume fractions with improved accuracy.

Full size image

5.3 Results on Real Data

On the two-shell clinical data, our method and the state-of-the-art approach by Jeurissen et al. [5] produced similar results. The estimated directions of up to three fibers with volume fractions above 0.1 are shown on a map of white matter volume fractions in Fig. 2(a/b), and exhibit little difference.

Fig. 2.
figure 2

On two-shell clinical data, similar results were obtained using a state-of-the-art approach (a) and ours (b), which is faster and can also be applied to DSI data, as demonstrated in (c).

Full size image

Averaged over the brain mask, the absolute deviation between tissue volume fractions estimated by the two methods was only 0.005 (CSF), 0.022 (GM), and 0.027 (WM). Averaged over the white matter, the angular deviation of fiber directions, weighted by their volume fractions, was \(7.98^\circ \), which is comparable to our simulation-based estimate of accuracy.

Since the true fiber directions are unknown in this case, we cannot be sure which method is more accurate in practice. However, a clear practical benefit of our method is its increased speed, and the fact that it can also be applied to data that has multiple b values, but no shell structure, as the DSI clinical data, for which results are shown in Fig. 2(c).

6 Conclusion

We introduced H-psd, a new positive definiteness constraint for spherical deconvolution, and showed that it is more stringent than usual non-negativity. It can be combined with all deconvolution methods, multi-tissue as well as the more widely used single-shell single-tissue variant [14]. We showed that the H-psd constraint increases accuracy at small angles, and is easy to enforce using convex cone programming libraries.

We also demonstrated that SHORE can be used as an extension of multi-tissue deconvolution [5]. This allowed us to apply multi-tissue deconvolution to DSI data, without sacrificing accuracy when working with data on shells.

Our method relies on the use of fourth-order tensors to describe fODFs. However, it is clear from the results (and was observed previously in [13]) that fourth-order is enough even for low angles and three-way crossings if we combine it with low-rank tensor approximation.

In the future, we will apply the H-psd constraint in the context of adaptive deconvolution [12] to improve per-voxel estimations of fiber response in patients with demyelinating disease. We expect that this will result in more accurate maps of tissue properties, and more reliable tractography.