Keywords

1 Introduction and Motivation for Research

Automatic Machine Learning (aML) is increasingly making big theoretical as well as practical advances in many application domains, for example, in speech recognition [1], recommender systems [2], or autonomous vehicles [3].

The aML-approaches sometimes fail or deliver unsatisfactory results, when being confronted with complex problem. Here interactive Machine Learning (iML) may be of help and a “human-in-the-loop" may be beneficial in solving computationally hard problems, where human expertise can help to reduce, through heuristics, an exponential search space.

We define iML-approaches as algorithms that can interact with both computational agents and human agents and can optimize their learning behaviour through these interactions [4]. To clearly distinguish the iML-approach from a classic supervised learning approach, the first question is to define the human’s role in this loop (see Fig. 1), [5].

Fig. 1.
figure 1

The iML human-in-the-loop approach: The main issue is that humans are not only involved in pre-processing, by selecting data or features, but actually during the learning phase they are directly interacting with the algorithm, thus shifting away the black-box approach to a glass-box; there might also be more than one human agent interacting with the computational agent(s), allowing for crowdsourcing or gamification approaches

Full size image

There is evidence that humans sometimes still outperform ML-algorithms, e.g. in the instinctive, often almost instantaneous interpretation of complex patterns, for example, in diagnostic radiologic imaging: A promising technique to fill the semantic gap is to adopt an expert-in-the-loop approach, by integrating the physicians high-level expert knowledge into the retrieval process and by acquiring his/her relevance judgments regarding a set of initial retrieval results [6].

Despite these apparent assumption, so far there is little quantitative evidence on effectiveness and efficiency of iML-algorithms. Moreover there is practically no evidence of how such interaction may really optimize these algorithms as it is a subject that is still being studied by cognitive scientists for quite a while and even though “natural” intelligent agents are present in large numbers throughout the world [7].

From the theory of human problem solving it is known that for example, medical doctors can often make diagnoses with great reliability - but without being able to explain their rules explicitly. Here iML could help to equip algorithms with such “instinctive” knowledge and learn thereof. The importance of iML becomes also apparent when the use of automated solutions due to the incompleteness of ontologies is difficult [8].

This is important as many problems in machine learning and health informatics are \(\mathcal{NP}\)-hard, and the theory of \(\mathcal{NP}\)-completeness has crushed previous hopes that \(\mathcal{NP}\)-hard problems can be solved within polynomial time [9]. Moreover, in the health domain it is sometimes better to have an approximate solution to a complex problem, than a perfect solution to a simplified problem - and this within a reasonable time, as an average medical doctor has on average less than five minutes to make a decision [10].

Consequently, there is much interest in approximation and heuristic algorithms that can find near optimal solutions within reasonable time. Heuristic algorithms are typically among the best strategies in terms of efficiency and solution quality for problems of realistic size and complexity. Meta-heuristic algorithms are widely recognized as one of the most practical approaches for combinatorial optimization problems. Some of the most useful meta-heuristic algorithms include genetic algorithms, simulated annealing and Ant Colony Optimization (ACO).

In this paper we want to address the question whether and to what extent a human can be beneficial in direct interaction with an algorithm. For this purpose we developed an online-platform in the context of our iML-project [11], to evaluate the effectiveness of the “human-in-the-loop” approach and to discuss some strengths and weaknesses of humans versus computers. Such an integration of a “human-into-the-loop” may have many practical applications, as e.g. in health informatics, the inclusion of a “doctor-into-the-loop” [12, 13] can play a significant role in support of solving hard problems, particularly in combination with a large number of human agents (crowdsourcing).

2 Background

2.1 Problem Solving: Human Versus Computer

Many ML-methods perform very badly on extrapolation problems which would be very easy for humans. An interesting experiment was performed by [14]: humans were presented functions drawn from Gaussian Processes (GP) with known kernels in sequence and asked to make extrapolations. The human learners extrapolated on these problems in sequence, so having an opportunity to progressively learn about the underlying kernel in each set. To further test progressive function learning, they repeated the first function at the end of the experiment, for six functions in each set. The authors asked for extrapolation judgements because it provides more information about inductive biases than interpolation and pose difficulties for conventional GP kernels [15].

Research in this area, i.e. at the intersection of cognitive science and computational science is fruitful for further improving aML thus improve performance on a wide range of tasks, including settings which are difficult for humans to process (for example big data and high dimensional problems); on the other hand such experiments may provide insight into brain informatics.

The first question is: When does a human still outperform ML-algorithms? ML algorithms outperform humans for example in high-dimensional data processing, in rule-based environments, or in automatic processing of large quantities of data (e.g. image optimization). However, ML-algorithms have enormous problems when lacking contextual information, e.g. in natural language translation/curation, or in solving \(\mathcal{NP}\)-hard problems. One important issue is in so-called unstructured problem solving: Without a pre-set of rules, a machine has trouble solving the problem, because it lacks the creativity required for complex problem solving. A good example for the literal competition of the human mind and its supposed artificial counterpart are various games, because they require human players to use their skill in logic, strategic thinking, calculating or creativity. Consequently, it is a good method to experiment on the strength and weaknesses of both brains and algorithms. The field of ML actually started with such efforts: In 1958 the first two programs to put the above question to the test were a checker program by Arthur Samuel and the first full chess program by Alex Bernstein [16]. Whilst Samuel’s program managed to beat Robert Nealey, the Connecticut checkers champion at that time, chess proved to be the computers weakness at that time; because on average just one move offers a choice of 30 possibilities, with an average length of 40 moves that leaves \(10^{120}\) possible games. Recently, computers had impressive results in competitions against humans: In 1997, the world chess champion Garry Kasparov lost a six-game match against Deep Blue. A more recent example is the 2016 Google DeepMind Challenge, a five-game match between the world Go champion Lee Sedol and AlphaGo, developed by the Google DeepMind team. Although AlphaGo won the overall game, it should be mentioned that Lee Sedol won one game. These examples just shall demonstrate how much potential a combination of both sides may offer [17].

As test case for our approach we selected the Traveling Salesman Problem, which is a classical hard problem in computer science and studied for a long time, and where Ant Colony Optimization has been used to provide approximate solutions [18].

2.2 Traveling Salesman Problem (TSP)

The TSP appears in a number of practical problems in health informatics, e.g. the native folded three-dimensional conformation of a protein is its lowest free energy state and both a two- and three-dimensional folding processes as a free energy minimization problem belong to a large set of computational problems, assumed to be very hard (conditionally intractable) [19].

The TSP basically is about finding the shortest path through a set of points, returning to the origin. As it is an intransigent mathematical problem, many heuristics have been developed in the past to find approximate solutions [20].

Numerical examples of real-world TSP tours are given in [21]; so, for example in Sweden for 24,978 cities the length is approximative 72,500 km [22] and in Romania: for 2950 cities, the length is approximative 21,683 km) [23]. The World TSP tour, with the length 7,516,353,779 km was obtained by K. Helsgaun using 1,904,711 cities [22].

The Mathematical Background of TSP. The TSP is a important graph-based problem which was firstly claimed to be a mathematical problem in 1930 [24]. Given a list of cities and their pairwise distances: find the shortest possible tour that visits each city exactly once. It is a \(\mathcal{NP}\)-hard problem, meaning that there is no polynomial algorithm for solving it to optimality. For a given number of n cities there are \((n-1)!\) different tours.

In terms of integer linear programming the TSP is formulated as follows [25–27].

The cities, as the nodes, are in the set \(\mathcal {N}\) of numbers \(1,\dots , n\); the edges are \(\mathcal {L}=\{(i, j): i, j \in \mathcal {N}, i \ne j\}\)

There are considered several variables: \(x_{ij}\) as in Eq. (1), the cost between cities i and j denoted with \(c_{ij}\).

$$\begin{aligned} x_{ij} = \left\{ \begin{array}{lr} 1,&{}\text{ the } \text{ path } \text{ goes } \text{ from } \text{ city } \text{ i } \text{ to } \text{ city } \text{ j }\\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$
(1)

The Traveling Salesman Problem is formulated to optimize, more precisely to minimize the objective function illustrated in Eq. (2).

$$\begin{aligned} \text{ min } \sum ^{n}_{i=1}{\sum ^{n}_{i\ne j,j=1}{c_{ij}x_{ij}}} \end{aligned}$$
(2)

The TSP constraints follow.

  • The first condition, Eq. (3) is that each node i is visited only once.

    $$\begin{aligned} \sum _{i\in \mathcal {N}, (i,j)\in \mathcal {L}}{x_{ij}}+\sum _{j\in \mathcal {N}, (i,j)\in \mathcal {L}}{x_{ji}}=2 \end{aligned}$$
    (3)

  • The second condition, Eq. (4), ensures that no subtours, \(\mathcal {S}\) are allowed.

    $$\begin{aligned} \sum _{i,j\in \mathcal {L}, (i,j)\in \mathcal {S}}{x_{ij}\le |\mathcal {S}|-1}, \forall \mathcal {S} \subset \mathcal {N}: 2\le |\mathcal {S}|\le n-2 \end{aligned}$$
    (4)

For the symmetric TSP the condition \(c_{ij}=c_{ji}\) holds. For the metric version the triangle inequality holds: \(c_{ik}+c_{kj}\ge c_{ij} , \forall i, j, k\) nodes.

3 Ant Algorithms

There are many variations of the Ant Colony Optimization applied on different classical problems. For example an individual ant composes a candidate solution, beginning with an empty solution and adding solution components iteratively until a final candidate solution has been generated [28]. The ants solutions are not guaranteed to be optimal and hence may be further improved using local search methods. Based on this observation, the best performance is obtained using hybrid algorithms combining probabilistic solution constructed by a colony of ants with local search algorithms as 2-opt, 3-opt, tabu-search etc. In hybrid algorithms, the ants can be seen as guiding the local search by constructing promising initial solutions. Conversely, the local search guides the colony evolution, because ants preferably use solution components which, earlier in the search, have been contained in good locally optimal solutions.

3.1 Ant Behaviour and Pheromone Trails

Ants are (similar as termites, bees, wasps) socially intelligent insects living in organized colonies where each ant can communicate with each other. Pheromone trails laid by foraging ants serve as a positive feedback mechanism for the sharing of information. This feedback is nonlinear, in that ants do not react in a proportionate manner to the amount of pheromone deposited, instead, strong trails elicit disproportionately stronger responses than weak trails. Such nonlinearity has important implications for how an ant colony distributes its workforce, when confronted with a choice of food sources [29].

This leads to the emergence of shortest paths and when an obstacle breaks the path, ants try to get around the obstacle randomly choosing either way. If the two paths encircling the obstacle have the different length, more ants pass the shorter route on their continuous pendulum motion between the nest points in particular time interval. While each ant keeps marking its way by pheromone the shorter route attracts more pheromone concentrations and consequently more and more ants choose this route. This feedback finally leads to a stage where the entire ant colony uses the shortest path. Each point at which an ant has to decide which solution component to add to its current partial solution is called a choice point.

The ant probabilistically decides where to go by favouring the closer nodes and the nodes connected by edges with higher pheromone trails. After the solution construction is completed, the ants give feedback on the solutions they have constructed by depositing pheromone on solution components which they have used in their solution. Solution components which are part of better solutions or are used by many ants will receive a higher amount of pheromone and, hence, will more likely be used by the ants in future iterations of the algorithm. To avoid the search getting stuck, typically before the pheromone trails get reinforced, all pheromone trails are decreased by a factor [30, 31].

Such principles inspired from observations in nature can be very useful for the design of multi-agent systems aiming to solve hard problems such as the TSP. Pioneer work in that respect was done by Marco Dorigo, the inventor of the Ant Colony Optimization (ACO) meta-heuristic for combinatorial optimization problems [32].

In summary it can be stated that ACO algorithms are based on simple assumptions:

  • Foraging ants construct a path in a graph and some of them (according to updating rules) lay pheromone trail on their paths

  • Decisions are based on pheromone deposited on the available edges and on the distance to the available nodes

  • Pheromone evaporates over time

  • Every ant remembers already visited places

  • Foragers prefer to follow the pheromone trails and to choose close nodes

  • Local information improve the information content of pheromone trails

  • The colony converges to a high quality solution.

Convergence is a core-competence of distributed decision-making by insect colonies; an ant colony operates without central control, regulating its activities through a network of local interactions [33]. The evolution in this case is a probabilistic stepwise construction of a path, making use of pheromones and problem-specific heuristic information to incrementally find a solution [34, 35].

ACO Procedure. Ant Colony Optimization (ACO) metaheuristic is a framework for solving combinatorial optimization problems. Depending on the specific problem tackled, there are many successful ACO realizations. One of the oldest and specifically dedicated to TSP is the Ant Colony System (ACS) [36]. In ACS, ants concurrently traverse a complete graph with n nodes, construct solutions and deposit pheromone on their paths. The distances between nodes are stored in the matrix \((d_{ij})\), and the pheromone on edges are in \((\tau _{ij})\).

The pseudocode of Ant Colony Systems is illustrated in Algorithm 1.

figure a

The characteristics of ACS are:

  • the decision rule for an ant staying in node i for choosing the node j is a mix of deterministic and probabilistic processes.

  • two rules define the process of pheromone deposit.

The most important ACS parameters are: the number of ants (m), the balance between the effect of the problem data and the effect of the pheromone (\(\beta \)), the threshold for deterministic decisions (\(q_{0}\)) and the evaporation rate of the pheromone (\(\rho \)). These parameters allow the following description of ACS.

At the beginning, a TSP solution is generated, using a heuristic method (for example, the Nearest Neighbor). At this step, this solution is considered the global best. The ants are deployed at random in the nodes and they move to other nodes, until they complete a solution. If an ant stays in the node i, it can move to one of the unvisited nodes. The available nodes form the set \( J_i\).

The next node j is chosen based on the pheromone quantity on the corresponding edge, on the edge’s length, and on an uniformly generated random value q \(\in [0,1]\). \(\eta \) is considered the inverse of the distance between two nodes. If \(q \le q_{0}\), then the Eq. (5) holds. Otherwise,j is randomly selected from the available nodes using a proportional rule, based on the probabilities (Eq. 6).

$$\begin{aligned} j =arg max_{l\in J_i} {( \tau _{il} \cdot [\eta _{il} ]^\beta )} \end{aligned}$$
(5)
$$\begin{aligned} p_{ij} = \frac{ \tau _{ij} \cdot [\eta _{ij} ]^\beta }{\sum _{l\in J_i}\tau _{il} \cdot [ \eta _{il} ]^\beta } \end{aligned}$$
(6)

After all the solutions are constructed, their lengths are computed, and the global best is updated, if a better solution is founded. The local pheromone update is applied. Each ant updates the pheromone on its path using Eq. (7).

$$\begin{aligned} \tau _{ij}(t+1) = (1 - \rho ) \cdot \tau _{ij}(t) + \rho \frac{1}{n \cdot L_{initial}} \end{aligned}$$
(7)

where \(L_{initial}\) is the length of the initial tour. The current iteration of the ACS is ended by applying the global pheromone update rule: Only the current best ant reinforces the pheromone on its path, using Eq. (8).

$$\begin{aligned} \tau _{ij}(t+1) = (1 - \rho ) \cdot \tau _{ij}(t) + \rho \frac{1}{ L_{best}} \end{aligned}$$
(8)

where \(L_{best}\) is the length of the best tour. The algorithm is repeated until the stopping conditions are met and exits with the best solution.

3.2 Inner Ant System for TSP

In [37] the Inner Ant System (IAS) is introduced, also known as Inner Update System in [38] where the “inner” rule was firstly introduced to reinforce the local search during an iteration. The structure of the IAS is similar with the Ant Colony System. After the inner rule the Lin-Kernighan 2-opt and 3-opt [39] are used to improve the local solution.

After each transition the trail intensity is updated using the inner correction rule, Eq. (9), from [38].

$$\begin{aligned} \tau _{ij}(t+1)=(1-\rho )\tau _{ij}(t)+\rho \frac{1}{n \cdot L^{+}} \end{aligned}$$
(9)

where \(L^{+}\) is the cost of the best tour.

In Ant Colony Systems only ants which generate an optimal tour are allowed to globally update the pheromone. The global update rule is applied to the edges belonging to the best tour. The correction rule is Eq. (8). In IAS the pheromone trail is over an upper bound \(\tau _{max}\), the pheromone trail is re-initialized as in [40]. The pheromone evaporation is used after the global pheromone update rule.

4 Experimental Method, Setting and Results

The ACO as an aML algorithm usually use no interaction. The ants walk around and update the global weights after each iteration. This procedure is repeated a distinct number of times. Following the iML-approach the human now can open the black-box and can manipulate this algorithm by changing the behavior of the ants. This is done by changing the pheromones, i.e. the human has the possibility to add or remove pheromones after each iteration.

4.1 Experimental Method

Based on the Inner Ant System for TSP this could be understood as adding or removing of pheromones on a track between cities. So the roads become more or less interesting for the ants and there is a high chance that they will consider road changes. In pseudocode we can write Algorithm 2.

figure b

For testing the Traveling Salesman Problem using iML we implemented an online tool with the following workflow:

\(\longrightarrow \) Click on the empty field to add new cities.

\(\longrightarrow \) Press “Start” to initialize the ants and to let them run.

\(\longrightarrow \) With a click on “Pause/Resume” the algorithm will be paused.

\(\longrightarrow \) Selection of two edges (first vertex and second vertex).

\(\longrightarrow \) Between these two edges the pheromones can be now adjusted by the slider below.

\(\longrightarrow \) With “Set Pheromone” changes of pheromones are written in the graph.

\(\longrightarrow \) Another click on “Pause/Resume” continues the algorithm.

\(\longrightarrow \) The steps above can be repeated as often as needed.

4.2 Implementation Details

The implementation is based on Java-Script. So it is a browser based solution which has the great benefit of platform independence and no installation is required.

For the test-setup we used 30 ants, 250 iterations. For the other parameters we choose fixed default values: \(\alpha \) =1; \(\beta \) =3; \(\rho \) =0.1. The parameters are in the current prototype fixed, this makes it easier to compare the results.

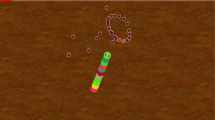
When starting the application an empty map appears on the left side. By clicking on the map a new city is created. The script automatically draws the connections between all the cities. After starting the algorithm, a list of cities/numbers will appear in the control center (see Fig. 2).

Fig. 2.
figure 2

The control-panel of our Java-Script code (Color figure online)

Full size image

After selecting two of them, the pheromones on the track between the cities can be adjusted with the slider. The current amount of pheromones is displayed as blue line with variance in the width for the amount of pheromones. After each iteration the current shortest path is calculated. If the new path is shorter than the old one, the green line will be updated. For the evaluation on testing process there are some pre-defined data sets. From these data sets the best solution is known. The original data sets can be found on [41].

The results of the pre-defined datasets can be compared with the optimal solution after finishing the algorithm by clicking on “Compare with optimal tour”. The optimal tour is displayed with a red line.

It is also possible to extend the existing data sets by adding points. A deletion of points is currently not possible, but we are working on it, as this allows a lot of interesting experiments (perturbation of graph structures). Saving and loading modules brings the benefit that the user can store and share the results if he discovered something interesting. During the loading the saved data is maximized to the size of the window.

4.3 Experimental Results

The update of the pheromones on a path changes the ant’s behavior. Because of human interaction such as adding pheromones the chances that an ant might take that path become higher. Consequently, this is a direct interaction with the algorithm. The interaction could not be effective through the evaporation of pheromones if this happens the user has to set pheromones again.

The interaction only changes the probability that the path could be taken. It has no effect on the shortest path. So it is obvious that a change of the pheromones may not necessarily result in a better path. An increase of this probability that it has an effect can be done by increasing the numbers of Iterations. If we take a closer look at our data set “14 cities in Burma”, Burma14.tsp, it is possible to see this effect. The path between city 1 and 10 is part of the shortest path (see Fig. 3).

Fig. 3.
figure 3

Not optimal path of Burma14.tsp dataset using an ant algorithm without iML after 250 iterations and using twenty ants.

Full size image

If we start the algorithm without interaction the probability that the shortest path is taken is very low. If we now increase some of our parameters like colony size (from 20 to 40) and the number of iterations (from 250 to 500), the chances become higher, that the algorithm will return the shortest path. When we now do the same with human interaction (add pheromones to path 1–10 and decrease pheromones on the surrounding paths), after iterations 10, 60, 100 and 150, then there is a high probability that the shortest path can be found in 250 iterations (see Fig. 4).

Fig. 4.
figure 4

Optimal path of Burma14.tsp dataset using iML, after 250 iterations including four human interactions and twenty ants for the ant algorithm.

Full size image

5 Discussion and Future Research

As we see in the test results above, the iML-approach poses benefits, however, further evaluations must also answer questions regarding the cost, reliability, robustness and subjectivity of humans-in-the-loop. Further studies must answer questions including: “When is it going to be inefficient?” In the example above the number of iterations can be reduced from 500 to 250, by three human interactions. The benefit is that after a few iterations the user can intuitively observe whether and to what extent ants are on a wrong way. The best number of cities, for an intuitively decision, is between about 10 and 150. A number beyond 150 cities poses higher complexity and prevent a global overview. An increase of the cities is possible, if there is for example a preprocessing phase of subspace clustering [42].

Further challenges are in the transfer of our approach to other nature inspired algorithms which have a lot of potential for the support of solving hard problems [43].

iML can be particular helpful whenever we are lacking large amounts of data, deal with complex data and/or rare events where traditional aML-algorithms suffer due to insufficient training samples. A doctor-in-the-loop can help where human expertise and long-term experience is useful, however, the optimal way will be in hybrid solutions in combining the “best of two worlds”, following the HCI-KDD approach [17, 44].

In the future it is planned to use gamification [45] and crowdsourcing [46], with the grand goal to make use of many humans to help to solve hard problems.

6 Conclusion

We demonstrated that the iML approach [5] can be used to improve current TSP solving methods. With this approach we have enriched the way the human-computer interaction is used [47]. This research is in-line with other successful approaches. Agile software paradigms, for example, are governed by rapid responses to change and continuous improvement. The agile rules are a good example on how the interaction between different teams can lead to valuable solutions. Gamification seeks for applying the Games Theory concepts and results to non-game contexts, for achieving specific goals. In this case, gamification could be helpful by considering the human and the computer as a coalition. There are numerous open research directions. The challenge now is to translate these approach to other similar problems, for example on protein folding, and at the same time to scale up on complex software applications.