Edge Directed Single Image Super Resolution Through the Learning Based Gradient Regression Estimation

Abstract

Single image super resolution (SR) aims to estimate high resolution (HR) image from the low resolution (LR) one, and estimating accuracy of HR image gradient is very important for edge directed image SR methods. In this paper, we propose a novel edge directed image SR method by learning based gradient estimation. In proposed method, the gradient of HR image is estimated by using the example based ridge regression model. Recognizing that the training samples of the given sub-set for regression should have similar local geometric structure based on clustering, we employ high frequency of LR image patches with removing the mean value to perform such clustering. Moreover, the precomputed projective matrix of the ridge regression can reduce the computational complexity further. Experimental results suggest that the proposed method can achieve better gradient estimation of HR image and competitive SR quality compared with other SR methods.

Z. Gan—This research was supported in part by the National Nature Science Foundation, P. R. China. (No. 61071166,61172118, 61071091, 61471201), Jiangsu Province Universities Natural Science Research Key Grant Project (No. 13KJA510004), Natural Science Foundation of Jiangsu Province (BK20130867), the Six Kinds Peak Talents Plan Project of Jiangsu Province ( 2014-DZXX-008), and the “1311” Talent Plan of NUPT.

1 Introduction

Image super resolution (SR) is a fundamental and significant issue in image processing community and computer vision applications. Generally, single image SR aims to recover a high resolution (HR) image from the low resolution (LR) one [1, 2]. The SR problem is inherently ill-posed given that many different HR images can produce the same LR image when blurred and down-sampled.

Currently, approaches solving the SR problem, can be classified into four categories, i.e., interpolation based, learning based, reconstruction based and edge directed (for a good survey see in [18]). Interpolation based approaches estimate the high-resolution image by interpolating the unknown pixels based on the surrounding known LR pixels, such as MSI [3] and SAI [4]. The underlying assumption of learning based approaches [5–9] is that there exists an inherent relationship between LR and HR image patch pairs. Then the relationship is learned and applied to a new LR image to recover its HR version. In addition, reconstruction based approaches highlight a reconstruction constraint and back-projection [10] is a classical reconstruction based one. Due to the jaggy or ringing artifacts of this method, many improvements have been made with different priors and regularization terms imposed [11–17]. The last category is about edge directed approaches. Edge directed approaches refer to the methods based on the edge models, where effective image edge priors [11–15] are enforced as a gradient domain constraint to estimate the target HR image, such as the edge smooth prior [14] or the gradient profile prior [11]. Thanks to the new algorithm, many scholars pay much attention to improve it. Adaptive gradient magnitude self-interpolation method GMSI [18] and cross-resolution sharpness preserving model DFSR [19] appear in succession.

Drawing a conclusion from previous work, instead of making use of gradient relationship between LR and HR image patch pairs, most edge directed methods estimate HR gradients of images according to edge pixels position or gradient magnitude for whole image. Motivated by it, we propose a novel edge directed image SR method by learning based gradient estimation. In particular, the gradient of HR image is estimated through using the example based ridge regression model. The main step of our method is about gradient regression estimation and reconstruction. The step about gradient regression estimation can further be divided into sample training and gradient estimation specifically. Recognizing that the training samples of the given sub-set for regression should have similar local geometric structure based on clustering, we employ high frequency of LR image patches with removing the mean value to perform such clustering. Moreover, the precomputed projective matrix of the ridge regression can reduce the computational complexity greatly. In reconstruction, the estimated gradient is regarded as a gradient constraint to guarantee that the result HR image preserves sharpness and refrains from artifacts such as jaggy and blurring. Experimental results suggest that the proposed method can achieve better gradient estimation of HR image and competitive SR quality compared with other SR methods. We will describe the main step of our method in detail in following section.

2 Edge Directed Single Image Super Resolution

In conventional SR problem [10–12], one LR image is modeled as the Gaussian blurred and down sampled one of its HR version. Namely, given a HR image $I_{h}$, a LR one $I_{l}$ is generated by

$$ I_{l} = (I_{h} *{\text{G}}) \downarrow_{s} $$

(1)

where $*$ is a convolution operator, $\downarrow$ is a down-sampling operation, s is a scaling factor, G is a blur kernel which is commonly approximated as a Gaussian function. The edge directed single image super resolution methods [11, 18] usually model the SR problem as Eq. 2, that is, given the LR image $I_{l}$ and the estimated HR gradient field $\nabla I_{h}^{T}$, $I_{h}$ can be reconstructed by minimizing the following energy function:

$$ I_{h}^{*} = \arg {\kern 1pt} \mathop {\hbox{min} }\nolimits_{{I_{h} }} E\left( {I_{h} |I_{l} ,\nabla I_{h}^{T} } \right) = E_{i} \left( {I_{h} |I_{l} } \right) + \beta E_{\text{g}} (\nabla I_{h} |\nabla I_{h}^{T} ) $$

(2)

where $E_{i} (I_{h} |I_{l} )$ is the reconstruction constraint in image domain, $E_{\text{g}} (\nabla I_{h} |\nabla I_{h}^{T} )$ is the gradient constraint in gradient domain, and parameter $\beta$ is a weighting constant to balance these two constraints as a trade-off. In experiments, a larger $\beta$ imposes more importance on the gradient domain, which contributes to producing sharp edges with little artifacts. Conversely, a smaller $\beta$ places much importance on the image domain, resulting in better image color and contrast, yet with ringing or jaggy artifacts along edges. The reconstruction constraint measures the difference between the LR image $I_{l}$ and the smoothed and down-sampled version of the HR image $I_{h}$, i.e.

$$ E_{i} \left( {I_{h} |I_{l} } \right) = |(I_{h} * {\text{G}}) \downarrow_{s} - I_{l} |^{2} $$

(3)

The gradient constraint requires that the gradient $\nabla I_{h}$ of the recovered HR image should be close to the estimated gradient $\nabla I_{h}^{T}$ as Eq. 4. This paper mainly focuses on the estimation of $\nabla I_{h}^{T}$, which will be presented in Sect. 3.1.

$$ E_{\text{g}} \left( {\nabla I_{h} |\nabla I_{h}^{T} } \right) = |\nabla I_{h} - \nabla I_{h}^{T} |^{2} $$

(4)

3 Proposed Edge Directed Super Resolution Method

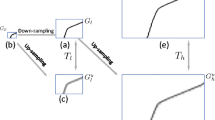
One motivation of our work is to estimate HR gradient of bicubic interpolated image patch with HR gradient of samples in the same cluster, based on the fact that image patches belonging to one cluster have similar local geometric structure. The main flow of our method is shown in Fig. 1, which includes gradient regression estimation and reconstruction.

Fig. 1.

Overview of our proposed method. First, bicubic interpolated image and its gradient is calculated. Second, HR gradient is estimated with regression coefficients and HR gradient of all samples. Last, the output image is reconstructed based on the edge directed SR model in Eq. 2 with the bicubic interpolated image as an initial.

Gradient regression estimation includes sample training and gradient estimation. First, in sample training (see Sect. 3.2), to generate meaningful clusters, we perform the clustering for image patches with removing their mean value. They are first classified into $s^{2}$ classes according to the central pixel position, where s is a scaling factor. Then K-means method is used to cluster patches into a lot of clusters for each class. After that, sparse filtering matrix W and sparse feature F is calculated for each cluster. Second, in gradient estimation, for each patch of high frequency in bicubic interpolated image, its sparse feature is calculated with sparse filtering matrix W. Then ridge regression method [7] is used to solve the coefficients of its sparse feature to all samples feature in the same cluster. And HR gradient of the patch is estimated with the coefficients and HR gradient of samples. In construction, the estimated gradient is regarded as the gradient domain constraint in the edge directed SR model as Eq. 2.

3.1 Gradient Regression Estimation of Super Resolution Image

Based on the fact that gradients of similar samples in one cluster are alike, we can estimate gradient of a patch by HR gradient of samples in the same cluster with their feature regression coefficients. Given a LR image $I_{l}$, we upsample it to obtain bicubic interpolated one $I_{bic}$. For patches whose variance is larger than a threshold ${\text{TH}}_{1}$ in $I_{bic}$, we perform our gradient estimation method to reduce computational complexity. And for the other patches, we use gradient of bicubic images instead. For each cropped image patch x with size $n \times n$ in $I_{bic}$, $\hat{\varvec{x}}$ is the high-frequency component as x minus its mean value u. Then we find the cluster that $\hat{\varvec{x}}$ belongs to by the standard of minimum Euclidean distance as Eq. 5 and calculate its sparse feature as Eq. 6

$$ k^{*} = \arg \;{\text{min }}_{k} \left\| {\hat{\varvec{x}} - {\text{C}}_{ck} } \right\|_{2}^{2} ,\;k = 1 \ldots K $$

(5)

$$ f = {\text{W}}_{{ck^{*} }} *\hat{\varvec{x}} $$

(6)

where ${\text{C}}_{ck}$ is cluster center of one cluster labeled by c and k (c and k is the label of cluster that will be introduced in Sect. 3.2), ${\text{W}}_{{ck^{*} }}$ is sparse filtering matrix of the cluster that $\hat{\varvec{x}}$ belongs to, f is feature of $\hat{\varvec{x}}$. Supposing there are N exemplar patches belonging to the cluster, then regression coefficients of feature f with all exemplar features can be formulated as:

$$ \varvec{\alpha}= \mathop {\hbox{min} }\nolimits_{\varvec{\alpha}} \left\| {f - {\text{F}}_{{ck^{*} }} \cdot\varvec{\alpha}} \right\|_{2}^{2} . $$

(7)

where ${\text{F}}_{{ck^{*} }} = [f_{1} ,f_{2} , \ldots ,f_{N} ] \in R^{m*N}$ is matrix of feature, ${\varvec{\upalpha}} = [\alpha_{1} ,\alpha_{2} , \ldots \alpha_{N} ] \in R^{1*N}$ is the vector of regression coefficients, m is feature dimension. For most clusters, number of exemplar patches is larger than feature dimension, which makes Eq. 7 an ill-posed problem. We can reformulate the problem as a least squares regression regularized by the $l_{2}$-norm of the coefficient vector ${\varvec{\upalpha}}$. Ridge regression [7] is used to solve the problem as Eq. 8:

$$ \varvec{\alpha}= \mathop {\hbox{min} }\nolimits_{\varvec{\alpha}} \left\| {f - {\text{F}}_{{ck^{*} }} \cdot\varvec{\alpha}} \right\|_{2}^{2} + \lambda \left\|\varvec{\alpha}\right\|_{2} $$

(8)

the parameter λ allows us to alleviate the ill-posed problem and stabilizes the solution of vector ${\varvec{\upalpha}}$. The solution is given by:

$$ \varvec{\alpha}= ({\text{F}}_{{ck^{*} }}^{T} \cdot {\text{F}}_{{ck^{*} }} +\uplambda{\text{I}})^{ - 1} {\text{F}}_{{ck^{*} }}^{T} f $$

(9)

where the projection matrix:

$$ {\text{T}} = ({\text{F}}_{{ck^{*} }}^{T} \cdot {\text{F}}_{{ck^{*} }} +\uplambda{\text{I}})^{ - 1} {\text{F}}_{{ck^{*} }}^{T} $$

(10)

then gradient can be estimated using the same coefficients on HR gradient of samples by (11) and (12)

$$ {\text{dx}} = {\text{DX}}_{{ck^{*} }} \cdot\varvec{\alpha}= \sum\nolimits_{j = 1}^{N} {(dx)_{j} \alpha_{j} } $$

(11)

$$ {\text{dy}} = {\text{DY}}_{{ck^{*} }} \cdot\varvec{\alpha}= \sum\nolimits_{j = 1}^{N} {(dy)_{j} \alpha_{j} } $$

(12)

where dx and dy is respectively estimated gradient in horizontal and vertical direction for the patch x,${\text{DX}}_{{ck^{*} }}$ and ${\text{DY}}_{{ck^{*} }}$ is respectively HR gradient matrix of all samples in these two directions, $(dx)_{j}$ and $(dy)_{j}$ is gradient of the j sample, which means that the estimated gradient is linear weighted sum of HR gradients of samples in the same cluster. For overlapped patches, two choices are alternative to estimate their gradients. First, only central pixel gradient is estimated. Second, we estimate gradient of each patch independently. Then to obtain the estimated image gradient, we average each pixel as it appears in the different patches. The second way yields better results so that we adopt it in our experiments. In implementation, in order to reduce the computational load, the projection matrix T is calculated offline, namely that we only need to multiply the precomputed projection matrix T with the sparse feature f.

3.2 Sample Training

(1) Clustering of Sample Sets.

Since natural images are abundant and easily acquired, we can assume that there are sufficient exemplar patches available for each cluster. Same with the gradient estimation step, only meaningful image patches whose variance is greater than ${\text{TH}}_{1}$ are selected.

Firstly, as shown in Fig. 2, for a scaling factor 3, only the pixels on position 1 in $I_{bic}$ are from LR image directly. While other pixels on positions 2–9 are interpolated by the surrounding pixels on position 1. Therefore overlapped patches in $I_{bic}$ can be classified into 9 classes centered by the 9 kinds of pixels. From each $I_{h}$ and the corresponding $I_{bic}$, a large set of patches ${\hat{\text{P}}}_{c} (c = 1, 2 , \ldots , 9)$ of $I_{bic}$ and corresponding HR gradient patches $\partial_{x} I_{h}$, $\partial_{y} I_{h}$ and can be cropped. For a patch ${\text{P}}_{c}$ in $I_{bic}$, we compute its mean value as μ and extract the feature ${\hat{\text{P}}}_{c}$ as the intensity ${\text{P}}_{c}$ minus μ. Denote the gradient field $\nabla I_{h} = \left( {\partial_{\text{x}} I_{h} ,\partial_{\text{y}} I_{h} } \right)$, the image $I_{h}$ is convolved respectively by discrete gradient operator $k_{1} = [ - \left( {1/2} \right), 0, (1/2)$ and $k_{2} = k_{1}^{T}$ to obtain $\partial_{\text{x}} I_{h}$ and $\partial_{\text{y}} I_{h}$. The similarity of two patches $p_{i}$ and $p_{j}$, is defined as $\updelta = \frac{{\left\| {p_{i} - p_{j} } \right\|_{1} }}{pixelnum}$. In order to avoid redundancy in one class, patches whose similarity is smaller than a threshold ${\text{TH}}_{2}$ are excluded.

Fig. 2.

Patches are classified into 9 classes by central pixel position for a scaling factor 3

Secondly, we adopt the K-means method to partition ${\hat{\text{P}}}_{c}$ into K clusters $\{ {\hat{\text{P}}}_{c1} ,{\hat{\text{P}}}_{c2} , \ldots ,{\hat{\text{P}}}_{cK} \}$ and denote by ${\text{C}}_{ck}$ the center of ${\hat{\text{P}}}_{ck}$. For given image patch, the most suitable cluster can be selected to estimate its HR gradient. Here K is usually set as integer power of 2 so that classification can be implemented with binary tree to improve efficiency.

(2) Feature of Image Patches.

Sparse filtering [20] is selected as the method of extracting feature, which is a simple but efficient algorithm with just one parameter. And the parameter presents the number of feature to learn. In order to learn the features of ${\hat{\text{P}}}_{c}$, we first note ${\hat{\text{P}}}_{c}$ as the data x. Supposing there are l LR exemplar patches belonging to the same cluster, feature of one sample is defined as soft-absolute function as Eq. 13, the sparse filtering objective function is as Eq. 14

$$\begin{aligned}&{\text{F}}_{j}^{(i)} = \sqrt {\varepsilon + ({\text{W}}_{j}^{T} \varvec{x}^{(i)} )^{2} } \approx |{\text{W}}_{j}^{T} \varvec{x}| \end{aligned}$$

(13)

$$\begin{aligned}&{ \hbox{min} } \sum\nolimits_{i = 1}^{l} {\left\| {{\hat{\text{F}}}^{(i)} } \right\|}_{1} = \sum\nolimits_{i = 1}^{l} {\left\| {\frac{{{\tilde{\text{F}}}^{i} }}{{\left\| {{\tilde{\text{F}}}^{i} } \right\|}}_{2} } \right\|}_{1} \end{aligned}$$

(14)

where ${\text{F}} \in R^{m*l}$ is feature matrix and W $\in R^{{m*n^{2} }}$ is sparse filtering matrix. Each row of F is a feature and each column is a sample, namely, each entry ${\text{F}}_{j}^{(i)}$ is the activity of feature j on sample i. For a cluster labeled by c and k, ${\hat{\text{P}}}_{ck}$ means LR patches, ${\text{DX}}_{ck}$ is horizontal HR gradient and ${\text{DY}}_{ck}$ represents vertical HR gradient. Meanwhile cluster centered noted as ${\text{C}}_{ck}$, ${\text{W}}_{ck}$ and ${\text{F}}_{ck}$ mean sparse filtering matrix and sparse feature matrix separately. Our training process is summarized in Algorithm 1 (Table 1).

Table 1. Main flow of sample training.

3.3 Reconstruction of Super Resolution Image

The estimated $\nabla I_{h}^{T}$ above is regarded as the gradient constraint in edge directed SR model as Eq. 2. The objective energy function Eq. 2 is a quadratic function with respect to $I_{h}$, therefore it is convex and the global minimum can be obtained by the standard gradient descent by solving the gradient flow equation. In our implementation, we use the following iterative schemes to optimize it:

$$ \begin{aligned} I_{h}^{t + 1} & = I_{h}^{t} - \tau \cdot \frac{{\partial E\left( {I_{h} |I_{l} ,\nabla I_{h}^{T} } \right)}}{{\partial I_{h} }} \nonumber\\ & = I_{h}^{t} - \tau \cdot \left[ {\left( {\left( {I_{h} * {\text{G}}} \right) \downarrow_{s} - I_{l} } \right) \uparrow_{s} * {\text{G}} - \beta ({\text{div}}\left( {\nabla I_{h} } \right) - {\text{div}}\left( {\nabla I_{h}^{T} } \right))} \right] \end{aligned} $$

(15)

where ${\text{div}}\left( {\nabla \cdot } \right) = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}$ is the Laplacian operator, ${\text{div}}\left( {\nabla I_{h} } \right) = \frac{{\partial (\partial_{\text{x}} I_{h} )}}{\partial x} + \frac{{\partial (\partial_{\text{y}} I_{h} )}}{\partial x}$. It can be carried out using standard finite difference scheme and $\tau$ is the step size.

4 Experiments

4.1 Settings

We select the Berkeley Segmentation Datasets [21] as our training set and test our method on a variety of natural images with rich edges. And 6 test examples are presented in Fig. 3. Note that, for color images, we transform them from RGB color space to YUV space. As human vision is more sensitive to luminance information, we only apply the proposed edge directed method on luminance channel (Y) and up-sample chrominance channels (UV) by bicubic interpolation. Finally, three channels are transformed into RGB as the final SR result. For a scaling factor 3, the patch size n is set as 11.

Fig. 3.

Six test example images (Color figure online).

Number of Clusters K:

Because of memory limitation (8 GB) of the computer, we randomly collected $10^{5}$ patches for 9 classes from the Berkeley Segmentation Datasets. The number of clusters is a trade-off between result quality and training computational complexity. In experiments, we compare super resolution results generated by 128 and 512 clusters. With more clusters, the most suitable cluster can be selected to estimate HR gradient for the given patch, so that the estimated gradient is close to HR gradient meanwhile high-frequency regions of the reconstructed image are better with less jaggy artifacts along edge. In other experiments, K is set as 512.

Parameters:

The standard variance of Gaussian blur kernel is set as 1.4 for a scaling factor 3. We set ${\text{TH}}_{1}$ and ${\text{TH}}_{2}$ as 10 and 0.2 separately and feature dimension m as 100 in sample training. In gradient estimation step, the results on different $\uplambda$ are stable and we set it as 50 in our experiments. In construction, in terms of the objective indicator and visual effect, $\beta$ and $\tau$ is respectively set as 0.1 and 1.5 with number of iterations set as 30.

4.2 Results

MSE between estimated gradient and HR gradient is calculated to evaluate their similarity and the fidelity of estimated gradient. We compare gradient MSE of results generated by 128 and 512 clusters. The gradient MSE results of bicubic, GMSI [18] and our method are listed in Table 2 and part images of estimated gradient maps are shown in Fig. 4. From Table 2, our error of estimated gradient is less than that of GMSI. With more clusters, the MSE are less. From Fig. 4, we can see the gradient of our method is sharper and much closer to the HR gradient compared to GMSI, because we estimate patch gradient with HR gradient of similar samples in the same cluster. Figure 9 shows one example results generated by 128 and 512 clusters with all the other same settings. As shown, edges of the reconstructed image are better with less jaggy artifacts along edge with more clusters.

Table 2. MSE of gradient compared to GMSI on six examples.

Fig. 4.

Comparisons of estimated gradient with GMSI [18] and bicubic. (a) Part of bicubic interpolated image. (b) The gradient field of images in (a) (MSE: 8.47). (c) Transformed gradient of GMSI [18] (MSE: 9.59). (d) Estimated gradient of our method (MSE: 6.17). (e) Ground truth gradient.

Fig. 5.

Results using different cluster number. (a) and (c) are estimated gradient and results generated by 128 clusters. (b) and (d) are generated by 512 clusters. (a) GMSE: 11.46. (b) GMSE: 10.98. (c) PSNR: 25.83 dB, SSIM: 0.880. (d) PSNR: 26.10 dB, SSIM: 0.889.

Fig. 6.

Super resolution comparison (3×) of other edge directed methods. (a) Bicubic upsample (31.39 dB/0.870). (b) Back-projection (33.09 dB/0.899) [10]. (c) GSMI (33.07 dB/0.892) [18]. (d) DFSR (32.74 dB/0.893) [19]. (e) Our method (33.56 dB/0.903). (f) Ground truth. The first line is gradient domain. Among them, (a), (b) and (d) is gradient of the image result. (c) and (e) are estimated gradient. (f) Ground truth gradient.

Fig. 7.

Super resolution comparison (3×) of other edge directed methods. (a) Bicubic upsample (25.630/0.767). (b) Back-projection (27.67 dB/0.837) [10]. (c) GSMI: (27.37 dB/0.820) [18]. (d) DFSR: (27.12 dB/0.827) [19]. (e) Our method (28.46 dB/0.845). (f) Ground truth. The first line is gradient domain. Among them, (a), (b) and (d) is gradient of the image result. (c) and (e) are estimated gradient. (f) Ground truth gradient.

Fig. 8.

Super resolution comparison (3×) of other edge directed methods. (a) Bicubic upsample (28.64 dB/0.8857). (b) GMSI (30.53 dB/0.913) [18]. (c) DFSR (30.44 dB/0.913) [19]. (d) Our method (31.29 dB /0.923). (e) Ground truth.

Fig. 9.

Super resolution comparison (3×) of other edge directed methods. (a) Bicubic upsample (23.27 dB/0.804). (b) GMSI (24.60 dB/0.859) [18]. (c) DFSR (25.70 dB/0.882) [19]. (d) Our method (26.10 dB/0.889). (e) Ground truth.

Moreover, the PSNR and SSIM [22] results are just calculated on Y channel, in order to measure the SR results qualitatively, which are separately listed in Tables 3 and 4. We compared our algorithm with IBP [10], GMSI [18], and DFSR [19]. Figures 6 and 7 present two comparisons of our method with GMSI and DFSR in gradient domain. As shown in these two figures, images are blurred by bicubic interpolation and jagged along edges by back-projection. GMSI method estimates a much sharper gradient domain, leading to edges of the reconstructed image sharper yet unnatural and artificial (refer to close-ups). The main reason is that the goal of GMSI is to obtain gradient domain which is sharper but not close to HR Gradient. Figures 8 and 9 present two examples with the two methods in image domain. As shown, the results of DFSR are very sharp, with rare ringing and blurring. However, unreal parts begin to appear and small scale edges are not well recovered. For example, eye area of Lady face seems to be very unreal and textures on Butterfly wing are less obvious. Compared to DFSR, our method recovers details better, especially on salient edges.

Table 3. PSNR measurement on six examples.

Table 4. SSIM measurement on six examples.

4.3 Complexity

In implementation, the projection matrix T in gradient regression estimation step is precomputed offline, meaning that we only need to multiply the precomputed projection matrix T with the sparse feature f. Therefore, the computation time is only linear multiplication and linear addition for a patch. The total computation complexity is linearly dependent on the number of high frequency patches in the bicubic interpolated image (Fig. 5).

5 Conclusion

In this paper, a novel edge directed image SR method by learning based gradient estimation has been presented. In proposed method, the gradient of HR image is estimated by using the example based ridge regression model. Considering the fact that the training samples of the given sub-set for regression should have similar local geometric structure based on clustering, we employed bicubic interpolated image patches with removing the mean value to perform clustering. Moreover, the precomputed projective matrix of the ridge regression reduced the computational complexity further. In reconstruction, the estimated gradient was regarded as the gradient constraint to guarantee that the result HR image preserves sharpness and refrains from artifacts. Experimental results showed that estimated gradient of our proposed method is much close to the ground truth and recovered image can preserve sharper edge compared with other SR methods.