Advance Reconnaissance and Optimal Monitoring

Abstract

Effective exploration techniques during mechanized tunneling are of high importance in order to prevent severe surface settlements as well as a damage of the tunnel boring machine, which in turn would lead to additional costs and a standstill in the construction process. A seismic methodology called full waveform inversion can bring a considerable improvement compared to state-of-the-art seismic methods in terms of precision. Another method of exploration during mechanized tunneling is to continuously monitor subsurface behavior and then use this data to identify disturbances through pattern recognition and machine learning techniques. Various probabilistic methods for conducting system identification and proposing an appropriate monitoring plan are developed in this regard. Furthermore, ground conditions can be determined by studying boring machine data collected during the excavation. The active and passive obtained data during performance of a shield driven machine were used to estimate soil parameters. The monitoring campaign can be extended to include above-ground structural surveillance as well as terrestrial and satellite data to track displacements of existing infrastructure caused by tunneling. The available radar data for the Wehrhahn-line project are displayed and were utilized to precisely monitor the process of anticipated uplift by injections and any subsequent ground building settlements.

2.1 Introduction

In mechanized tunneling, which is a highly automated process, a tunnel boring machine (TBM) sequentially excavates the ground and installs the tunnel lining. The high level of automation causes restrictions for a dynamic adaptation of the construction process and makes it vulnerable for unconsidered events. Sudden geological changes may endanger the process of tunnel construction by causing unexpected surface settlements, damage to the TBM or wear of the cutting tools. Since there is only a limited access to the front shield of the TBM during the construction, its maintenance turns out to be cumbersome. Furthermore, damage of the TBM leads to construction delays which may cause accumulation of running costs (e.g. personnel costs). Early identification of geological changes enables the opportunity to initiate countermeasures by, for instance, adapting the excavation velocity, changing the cutting tools or adapting the face pressure. During the planning as well as the construction phase, exploratory drilling is typically performed to characterize properties of the ground. However, such drilling is not sufficient for estimation of the subsoil properties along the whole tunnel track since it is locally limited.

Approaches that are suitable for exploring the space directly in front of the tunnel face are provided by exploration seismics. However, state-of-the-art methods only process the onsets of directly reflected waves and therefore neglect information of later arriving waves. In order to improve today’s exploration techniques, the application of a methodology called full waveform inversion (FWI) is proposed. Here, the whole information of the seismic records is taken into account. Different FWI approaches are proposed, investigated and validated with synthetic data and experimental laboratory data in Sect. 2.2.

Another possibility for exploration during mechanized tunneling is to analyze the gathered hydro-mechanical data during the excavation process. Measuring the changes of surface settlement or pore water pressure in various locations around the tunnel line is a common practice, and through analyzing these data the geotechnical pattern of the subsoil can be recognized. Therefore, a pattern recognition approach based on supervised machine learning is proposed and investigated in Sect. 2.3. To evaluate the surrounding geomaterial based on the measurements, one should carefully consider the associated aleatory and epistemic uncertainties in such problems. Uncertainties in geomaterials are mainly due to their geologic origin, which implies their heterogeneity as well as multiphase-nature at different aggregation states. Furthermore, the boundary conditions are frequently complicated as a result of multi-phase interactions in projects such as tunneling, making the conventional approaches of using soil sample and preliminary laboratory studies on limited number of samples to predict soil parameters less trustworthy. The impact of uncertainties on tunneling performance may be precisely assessed utilizing the model adaptation approach, which is primarily concerned with the use of previously acquired datasets in the subsequent prediction and TBM steering process. In this regard, various uncertainty quantification methods like sensitivity analysis, random field and back analysis were employed.

Afterwards, a scenario-based framework pattern recognition is used to explore the geological formation ahead of TBM based on the subsoil response to the excavation process. It takes into account several frequent geometrical variations of geological scenarios in tunnel construction, such as layer change, interlayers, or a large rock boulder. As a result, in the context of pattern identification, machine learning algorithms are used to identify critical changes in geological conditions, such as incoming new soil layers or enormous rock boulders.

Besides obtained data by sensors and gauges in the subsoil, TBMs constantly monitor several variables during excavation. Therefore, one may determine ground conditions by analyzing such machine data. Among all the monitored data, data on the movement of the cutting wheel and the shield in relation to subsoil conditions for a shield driven TBM, in particular, can be considered as formative data. Parameters as thrust force on cutting wheel, torque on cutting wheel and advance speed are referred to as excavation-specific data components, and they may be used as indicators for the Earth’s resistance to excavation (ground conditions) and the condition of the cutting wheel (wheel design, tool wear, and clogging), accordingly. The relation between different parameters on various projects and their effectiveness are studied in the Sect. 2.5.

A comprehensive monitoring campaign, which is required to prevent any unexpected or serious damage to above-ground structures, may include the use of available radar data and terrestrial technologies for the above-ground observations in addition to subterranean monitoring. Terrestrial settlement monitoring includes measurements of the interplay of all (settlement) data prior to, during, and after tunnel construction. The data delivered by these technologies may be detailed to the millimeter level for monitoring the settlement or tilting of buildings in the impacted geographical extent of tunnel excavation. Using the radar data, on-site installations, such as those found in buildings, are no longer necessary. The technology captures complicated raw data signals (amplitude and phase information) provided by radar waves (electromagnetic waves) reflect on the upper mantle. These data can be utilized in visualization process besides the actual settlement monitoring. Visualized in space and time, critical conditions such as torsional deformations when underpassing structures in parallel can be recognized easier. Details about the above-ground monitoring methods and data is presented in Sect. 2.6. The following section offers a case study of monitoring displacements of existing infrastructure caused by the excavation of the Wehrhahn railway tunnel in Dusseldorf using a series of 16 TerraSAR-X photos.

2.2 Seismic Reconnaissance

Triggered by man-made explosions or natural earthquakes, energy is induced into the ground and travels through it in the form of seismic body waves. These waves have different propagation modes, e.g. compressional waves that vibrate in propagation direction and shear waves that vibrate perpendicular to the propagation direction. The propagation velocity of the different waves depends on the elastic properties of the ground. These are, in the context of seismological applications, usually described in terms of the compressional wave velocity $v_{\text{p}}$ (or P-wave velocity) and the slower shear wave velocity $v_{\text{s}}$ (or S-wave velocity),

$$\displaystyle v_{\text{p}}=\sqrt{\frac{E\left(1-\nu\right)}{\rho\left(1+\nu\right)\left(1-2\nu\right)}}\,,\qquad v_{\text{s}}=\sqrt{\frac{E}{2\rho\left(1+\nu\right)}}\,,$$

(2.1)

rather than in terms of Young’s modulus $E$ and Poisson’s ratio $\nu$. The density of the ground is denoted by $\rho$. Waves that encounter a stress free surface, e.g. the Earth’s surface, are to some part reflected. Another portion of these waves induces surface waves with very high amplitudes that propagate along the surface with a velocity slightly lower than the shear wave velocity. At geological interfaces, reflections, refractions and conversions of the seismic waves occur, whereby the amount of reflected, refracted and converted energy as well as the refraction angle depends on the material contrast.

The physical behavior of the ground can be described by the elastic wave equation

$$\displaystyle\rho(\mathbf{x})\,\ddot{\mathbf{u}}(\mathbf{x},t)-\nabla\cdot\left(\mathsf{C}(\mathbf{x}):\nabla\mathbf{u}(\mathbf{x},t)\right)=\mathbf{f}(\mathbf{x},t),$$

(2.2)

where $\mathsf{C}(\mathbf{x})$ is the fourth-order material stiffness tensor which contains the elastic properties of the ground at the spatial position $\mathbf{x}$. The external force vector at the time $t$ is denoted by $\mathbf{f}(\mathbf{x},t)$ whereas the displacement vector is denoted by $\mathbf{u}(\mathbf{x},t)$ and its second derivative with respect to time by $\ddot{\mathbf{u}}(\mathbf{x},t)$.

For exploration in tunneling, a non-destructive artificial signal is induced into the ground. A wave propagation scenario within a two-dimensional tunnel environment with a disturbance in front of the tunnel is illustrated by Fig. 2.1 for two different points in time.

Fig. 2.1

A horizontal single-force source (triangle) at the tunnel face emits a Ricker wavelet with a peak frequency of 500 Hz. The vibration direction and amplitude of the waves are indicated by the red arrows. A rectangular shaped disturbance (indicated by its borders) with lower P- and S-wave velocities is located in front of the tunnel. The reflection of the first P-wave at the Earth’s surface can be observed in the left picture. The right picture illustrates the induced surface waves at the Earth’s surface as well as the interaction of the waves with the disturbance

The emitted seismic waves interact with anomalies and arrive at the geophones, which record the signal. The gained seismic records contain information about the geological conditions of the ground. Seismic exploration approaches utilize this information for the purpose of inferring the structure of the ground.

2.2.1 State-of-the-art Methods for Seismic Exploration in Mechanized Tunneling

State-of-the-art methods for seismic reconnaissance during mechanized tunneling are based on tomography methods. Certain parts of the seismic waveforms are evaluated, where most commonly reflected P-waves are extracted and processed for the purpose of estimating anomaly locations and properties. Two exemplary systems which are used in practice are Sonic Softground Probing (SSP) [49] and Tunnel Seismic Prediction (TSP) [92]. SSP is used for reconnaissance in soft rock. Sources and receivers are placed at the cutting wheel of the TBM and in the case that reflected waves arrive at the receivers, they are extracted from the waveform and evaluated with migration techniques. The range of SSP is specified to lie at about 40 m [101]. In TSP, sources and receivers are placed in boreholes along the tunnel wall. Also here, reflected waves are analyzed and evaluated using various geotechnical approaches. TSP’s range is given with about 150-200 m; however, the error margin increases rapidly with increasing distance to the TBM shield [20]. A methodology which is generally able to provide a detailed image of the subsoil is the concept of full waveform inversion (FWI). The method can be expected to outperform the state-of-the-art systems in terms of ranges, error margins and levels of detail since not only parts of the acquired waveforms are evaluated, but the full measured signal.

2.2.2 Full Waveform Inversion

One of the first FWI approaches is introduced by Tarantola [110, 111] for acoustic as well as elastic media. For FWI, a numerical model is set up which is able to approximate forward wave propagation described by the elastic wave equation (Eq. 2.2). The ground properties (e.g. expressed by the P-wave velocity $v_{\text{p}}$, the S-wave velocity $v_{\text{s}}$ and the density $\rho$) are discretized for the numerical application and the corresponding parameters which specify the ground model can be stored in a model $\mathbf{m}$.

The goal of FWI is to minimize the difference of the synthetic seismic records and the seismic records from field observations by adapting the ground properties $\mathbf{m}$ of the numerical model iteratively. The ground model which produces the lowest difference of the seismic data is assumed to be a good representation of the real ground. Since different ground formations are able to produce similar seismic records, FWI has to deal with the ambiguity of the inverse problem. For that purpose, all prior information (e.g. from exploration drilling, other exploration approaches or former construction projects) can be used to define an initial model which is close to the real subsurface in order to move the inversion to reconstruct a physically meaningful ground model. Or, in different approaches, prior knowledge may be used to implement a parametrization of the ground model directly. Different objective functions can be used to quantify the difference of the seismic records which have, depending on the FWI application, different advantages and disadvantages [13]. The least squares norm is commonly used as misfit function,

$$\displaystyle\chi(\mathbf{m})=\frac{1}{2}\sum_{s=1}^{N_{\text{s}}}\sum_{r=1}^{N_{\text{r}}}\,\int\limits_{T}\!\left(u_{r}^{s}(t;\mathbf{m})-\bar{u}_{r}^{s}(t)\right)^{2}\mathrm{d}t.$$

(2.3)

The considered time interval is denoted by $T$, the approximated displacements of the current ground model $\mathbf{m}$ by $u_{r}^{s}(t;\mathbf{m})$ and the displacements from the field observations by $\bar{u}_{r}^{s}(t)$. The squared difference is summed over the number of all receivers $N_{\text{r}}$ and the number of all sequentially used sources $N_{\text{s}}$.

In the last decades, many different approaches of FWI have been developed, e.g. adjoint time and frequency domain approaches, statistical FWI approaches or machine learning approaches. There exist many different successful applications of FWI, even on the continental scale (e.g. [128]). However, FWI has not been applied yet for reconnaissance in mechanized tunneling projects.

A high number of forward simulations is needed for FWI due to its iterative procedure. Therefore, a real time application with three-dimensional tunnel models is not feasible with nowadays computational resources. Since the efficiency of computational techniques and resources have increased enormously in the last decades, it can be expected that an application of FWI will become practicable in the future. Therefore, an early investigation of the potential of FWI for reconnaissance in mechanized tunneling is necessary. Due to the variety of FWI approaches, an investigation on their characteristics for different ground conditions and scenarios is recommendable.

In Sect. 2.2.3, two Bayesian FWI approaches for application in mechanized tunneling are presented. The application of adjoint inversion approaches is examined for a time domain approach in Sect. 2.2.4 and for a frequency domain approach in Sect. 2.2.6, where synthetic reference data is used for inversion. However, also a validation of the proposed inversion schemes with measured data is crucial. Since seismic measurements during today’s tunneling projects are not performed for FWI but for other exploration approaches and since rich field data, suitable for FWI, is difficult to get, a small-scale experiment is constructed in order to acquire seismic data with which some of the proposed inversion approaches are validated (Sect. 2.2.7). The validation with this experimental laboratory is valuable since severe measurement and later modeling errors are included in the inversion. Furthermore, small heterogeneities inside the specimen may be expected to have a large scattering effect on the small-scale, but a vanishing effect in later tunneling scenarios, which makes the inversion even more challenging on the small-scale concerning that point. Therefore, the validation of the methods by the acquired experimental data is evaluated to be reliable.

2.2.3 Bayesian Full Waveform Inversion

Instead of allowing the material properties to vary all over the model domain like in the upcoming adjoint methods, the dimensionality of the inverse problem can be aimed to be reduced. Dimensionality reduction can be achieved by either implementing a generally suitable but simplified parametrization of the subsoil model or even a direct parametrization (e.g. of a boulder or a layer change) which is based on prior knowledge. The search for a set of parameters with a misfit value close to the global minimum can then be performed with Bayesian inference. In this approach, a prior guess with initial uncertainties is specified. Parameter configurations are sampled and the prior guess and uncertainties are multiply updated. The output is a statistical description of the model parameters, revealing the sampled parameter configuration which is most likely representing the true subsurface. Furthermore, uncertainty quantification can be performed in order to find out at which positions anomalies could potentially be missed. If the parametrization can approximately describe the real subsurface, the proposed Bayesian FWI approaches can deliver precise results, which will be shown in the further progress of the chapter.

Two methods are proposed, where both approaches include the unscented Kalman filter (UKF) that is based on Bayesian inference. The first method is called unscented hybrid simulated annealing (UHSA) [80] and the second method is called the UKF-controlled parametric level-set method (UKF-PaLS) [79]. In this section, the working principles of UHSA and UKF-PaLS are briefly explained in words and UKF-PaLS is validated with synthetic data. For a complete description of the two methods, readers are referred to [114].

2.2.3.1 Unscented Hybrid Simulated Annealing (UHSA)

UHSA is a global optimization algorithm which combines the UKF [39] with simulated annealing (SA) [47]. The method is based on implementing prior knowledge in the form of a user-defined parametrization of the disturbance. Commonly, a coarse representation of the subsoil is already available after planning of the tunneling track, e.g. from exploratory drillings, prior seismic surveys, geological maps, or other exploration techniques. Then, for instance, if prior knowledge exists that there is a cuboid boulder somewhere in the model domain, one could define the parametrization with its center location coordinates, three edge lengths and the material properties. With respect to the parametrization, UHSA conducts a global search in order to investigate the whole parameter space. In the course of this, SA acts as the global search algorithm, proposing certain parameter configurations and UKF acts as the local search algorithm, performing a local minimization for some of those parameter configurations, where parameter configurations with comparatively small misfit functionals are more frequently chosen as a starting point for local minimization. Due to the strong dimensionality reduction, results of UHSA can be close to exact if the chosen parametrization of the disturbance is sufficient; even when experimental scenarios are considered [115, 116] or when the parametrization is not fully correct [88]. UHSA results will be demonstrated on experimental examples directly in Sect. 2.2.7.1 and Sect. 2.2.7.2.

2.2.3.2 UKF-Controlled Parametric Level-Set Method (UKF-PaLS)

The previously described method can only be applied if prior knowledge is available, which is different for UKF-PaLS. In this method, the parametric level-set method (PaLS) enables a parametrization of the disturbance domain. Radial basis functions, also called bumps, are used to define the geometry of irregularly shaped objects. Prior to inversion, the centers of the bumps are defined by the user. Placing the bumps, a region of investigation as well as a resolution is defined, where at this stage, also prior knowledge can be included. Each radial basis function is controlled by two parameters, where one parameter basically defines the radial size of the bump, and the other parameter distorts the shapes of the bumps. The UKF seeks to find the optimal configuration of level-set parameters and material properties. In order to facilitate the finding of a parameter configuration corresponding to a misfit functional which is close to the global optimum, a multi-scale approach is implemented (see e.g. [26]). This approach includes a low-pass filter with a stepwise increasing cutoff frequency into the inversion. In early iterations, the simulation and measurement data is filtered with a low cutoff frequency in order to resolve larger structures, while in later iterations, higher cutoff frequencies are used in order to resolve more details.

Fig. 2.2

True model (left) and initial UKF-PaLS model (right). Ticks are in distances of 10 m. In the left figure, the double standard deviations of the initial parameters are illustrated by the medium dark gray tone (see marking)

For UKF-PaLS, a 2D synthetic inversion scenario is presented. For more 2D as well as 3D examples, readers are referred to [114]. The computational model used for generating the synthetic measurements is shown in Fig. 2.2, left. Simulations are conducted with the spectral-element code specfem2D [118]. Two rectangular disturbance domain objects are located close to each other with higher wave velocities than the wave velocities of the background domain, where the material is considered elastic with no attenuation for both sets of material properties. The density is considered constant all over the model domain. The top surface and all tunnel walls obtain free boundary conditions, while the other model boundaries obtain absorbing boundary conditions. The initial UKF model is shown in Fig. 2.2, right. 28 bumps are aligned on a regular grid, so that $2\times 28=56$ level-set parameters and two material properties are to be determined during inversion. The initial level-set parameters are chosen so that small areas of the disturbance material are visible. In order to perform uncertainty quantification, the double standard deviation of the initial covariance matrix of the model parameters is computed and illustrated by the medium dark gray tone (see marking). Note that for the initial model, this measure does not allow for any physical interpretation.

Fig. 2.3

Estimates corresponding to the minimum misfit. The medium dark gray regions illustrate the double standard deviations of the computed covariance matrix of the model parameters. Ticks are in distances of 10 m. Sources illustrated by red dots, receivers illustrated by green dots

The inversion method is tested with two different source-receiver configurations, which are visualized together with the inversion results in Fig. 2.3 by the red (sources) and green (receivers) dots. Both configurations include 2 sources placed at the tunnel front and 7 receivers placed inside the tunnel at the front and walls. One configuration additionally includes 9 receivers located at the Earth’s surface (compare Fig. 2.3, left). With both source-receiver configurations, a precise estimation of the reference model is achieved, where both objects are clearly resolved without melting together. All front and rear boundaries seen from the tunnel are well reconstructed. Due to the lack of receivers at the Earth’s surface, top and bottom borders are slightly less precisely determined for the example shown in Fig. 2.3, right. However, differences remain small. The high precision emphasizes the gain of the dimensionality reduction since especially the resolving of rear boundaries based only on reflected waves is a difficult FWI challenge. The uncertainties which are again visualized by the medium dark gray areas show where objects are most probably missed by the inversion, where the greatest uncertainties lie in the ‘‘shadow’’ of the reconstructed objects.

2.2.4 Adjoint Time Domain Full Waveform Inversion

This section gives an overview of the implementation of the adjoint time domain inversion method into the nodal discontinuous Galerkin solver nexd [54]. The solution of the forward problem is introduced briefly, the adjoint time domain inversion method is introduced and examples for a successful inversion in 2D and 3D are given.

2.2.4.1 Forward Problem

The solution of the forward problem is an essential part of the inversion process as it has to be performed multiple times during each iteration step. In this approach the discontinuous Galerkin (DG) solver nexd developed by [53] is used to perform these calculations. nexd is based on a velocity-stress formulation of the wave equation derived by [42] and [43]. The computational model of the target region is divided into triangular or tetrahedral elements and the solution vector containing stress and particle velocity components is expanded into appropriate basis functions defined on the elements. By multiplying with a set of test functions defined on the elements and integrating over each element, the elastic wave equation is replaced by a large coupled system of ordinary differential equations. Interaction and coupling between elements is realized by numerical fluxes. Depending on the choice of basis functions, DG methods are either of modal or nodal type. Modal approaches use sets of orthogonal basis functions whereas nodal ones take multidimensional Lagrange interpolating polynomials anchored to carefully selected nodal points [31]. In the latter case, the expansion coefficients are identical to the values of the velocity-stress vector at the nodal points. As nexd is based on the nodal version of the DG method, a quick overview of the semi-discrete scheme is given: Let now $l_{i}(\mathbf{x})$ denote the Lagrange polynomials attached to the nodes $\mathbf{x}_{i}$ [31]. Moreover, let $\mathbf{q}(\mathbf{x}_{j},t)$ denote the solution vector in element $k$, representing the values of the stress and particle components at node $\mathbf{x}_{j}$.¹ Then, using the Einstein summation convention, the system of ordinary differential equations for the expansion coefficients can be written as

$$\begin{aligned}\mathbf{M}^{k}_{ij}\frac{\partial}{\partial t}\mathbf{q}(\mathbf{x}_{j},t)= & {-\mathbf{A}}\mathbf{S}^{k}_{ij,x}\mathbf{q}(\mathbf{x}_{j},t)-\mathbf{B}\mathbf{S}^{k}_{ij,y}\mathbf{q}(\mathbf{x}_{j},t)-\mathbf{C}\mathbf{S}^{k}_{ij,z}\mathbf{q}(\mathbf{x}_{j},t)\end{aligned}$$

$$\begin{aligned} & +\mathbf{M}^{k}_{ij}\mathbf{s}(\mathbf{x}_{j},t)-\int_{\partial D^{k}}\mathbf{r}_{\text{n}}(\mathbf{x},t)\,l_{i}(\mathbf{x})\,d\Sigma,\quad 1\leq i,j\leq N_{\text{p}}\,,\end{aligned}$$

(2.4)

where $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ are matrices containing the material properties of each element, $\mathbf{M}^{k}$ is the mass matrix, $\mathbf{S}^{k}_{x}$, $\mathbf{S}^{k}_{y}$ and $\mathbf{S}^{k}_{z}$ are the stiffness matrices, $\mathbf{r}_{\text{n}}(\mathbf{x},t)$ are normal Riemann fluxes and $\mathbf{s}(\mathbf{x}_{j},t)$ is the source term. The number of interpolation points per element is denoted by $N_{\text{p}}$ and $\partial D^{k}$ denotes a line element of an element edge. Equation 2.4 is a system of coupled ordinary differential equations, as the flux terms depend on the expansion coefficients of adjacent elements. A more comprehensive derivation of Eq. 2.4 is given in [53, 54].

2.2.4.2 Adjoint Inversion

The primary ingredient for the inversion process is the measured data, since this data contains the information on the model that is to be calculated during the inversion process. This data is either generated synthetically using a forward solver, e.g. specfem or nexd, or data from seismic stations deployed in the field is used. The goal of the inversion process is to recover the model $\mathbf{\bar{m}}$, that best explains the observed data.

The search for the best model $\mathbf{\bar{m}}$ starts with a model $\mathbf{m}_{0}$ for which synthetic waveforms $\mathbf{u}_{r}^{s}(t,\mathbf{m}_{0})$ are to be calculated by a forward simulation. These synthetic waveforms are compared to the observed ones, $\mathbf{\bar{u}}$ and the misfit between the observed and measured seismograms is calculated according to Eq. 2.3. The model $\mathbf{m}_{0}$ is adjusted iteratively into models $\mathbf{m}_{j}$ with waveforms $\mathbf{u}_{r}^{s}(t,\mathbf{m}_{j})$ at iteration $j$ where $\mathbf{m}_{j}$ should approach $\mathbf{\bar{m}}$ with increasing $j$ in the sense of minimizing the misfit between synthetic and observed waveforms as defined by [119].

To minimize the misfit $\chi$ an iterative approach is used which exploits information about the misfit gradient [118]. The latter is obtained by taking the Fréchet derivative of Eq. (2.3) with respect to $\mathbf{m}$,

$$\begin{aligned}\frac{\partial\chi}{\partial\mathbf{m}}= & \sum\limits_{s=1}^{N_{\text{s}}}\sum\limits_{r=1}^{N_{\text{r}}}\int\limits_{T}\left(\mathbf{u}^{s}_{r}(t,\mathbf{m})-\mathbf{\bar{u}}^{s}_{r}(t)\right)\cdot\frac{\partial\mathbf{u}_{r}^{s}(t,\mathbf{m})}{\partial\mathbf{m}}\,\mathrm{d}t\,.\end{aligned}$$

(2.5)

Calculating the Fréchet derivatives of the wavefield with respect to $\mathbf{m}$, $\partial\mathbf{u}/\partial\mathbf{m}$, for all variations of $\mathbf{m}$ would require large amounts of storage. Instead, [26] shows that the misfit gradient can be more efficiently calculated with the help of an adjoint wave field $\mathbf{u}^{\dagger}(\mathbf{m},\mathbf{x}_{i},T-t)$, which in turn can be obtained as the time reversed result of a forward simulation with so-called adjoint sources situated at the receiver positions and defined by

$$\begin{aligned}\mathbf{f}^{\dagger}(\mathbf{m},\mathbf{x}_{i},t)=\mathbf{u}_{r}^{s}(T-t,\mathbf{m})-\mathbf{\bar{u}}_{r}^{s}(T-t)\,.\end{aligned}$$

(2.6)

Thus, the adjoint sources are the time reversed residuals between observed and predicted waveforms injected at the receiver positions and propagated into the medium.

For a perturbation of density and Lamé parameters in the subsurface, $\Updelta m=(\Updelta\rho,\Updelta\lambda,\Updelta\mu)$, the change of misfit is given by

$$\begin{aligned}\Updelta\chi & =\int\limits_{V}\frac{\partial\chi}{\partial\rho}\Updelta\rho+\frac{\partial\chi}{\partial\lambda}\Updelta\lambda+\frac{\partial\chi}{\partial\mu}\Updelta\mu\,\mathrm{d}V\end{aligned}$$

$$\begin{aligned} & =-\int\limits_{V}K_{\rho}\frac{\Updelta\rho}{\rho}+K_{\lambda}\frac{\Updelta\lambda}{\lambda}+K_{\mu}\frac{\Updelta\mu}{\mu}\,\mathrm{d}V\,,\end{aligned}$$

(2.7)

where the misfit kernels are introduced according to [56] as

$$\begin{aligned}K_{\rho}(\mathbf{x}):=-\rho\frac{\partial\chi}{\partial\rho} & =-\int\limits_{0}^{T}\rho(\mathbf{x})\mathbf{u}^{\dagger}(\mathbf{x},T-t)\cdot\partial^{2}_{t}\mathbf{u}(\mathbf{x},t)\,\mathrm{d}t,\end{aligned}$$

$$\begin{aligned}K_{\lambda}(\mathbf{x}):=-\lambda\frac{\partial\chi}{\partial\lambda} & =-\int\limits_{0}^{T}\lambda(\mathbf{x})(\mathop{\mathrm{Tr}}(\boldsymbol{\epsilon}^{\dagger}(\mathbf{x},T-t)))(\mathop{\mathrm{Tr}}(\boldsymbol{\epsilon}(\mathbf{x},t)))\,\mathrm{d}t,\quad\text{and}\end{aligned}$$

$$\begin{aligned}K_{\mu}(\mathbf{x}):=-\mu\frac{\partial\chi}{\partial\mu} & =-\int\limits_{0}^{T}2\mu(\mathbf{x})\boldsymbol{\epsilon}^{\dagger}(\mathbf{x},T-t):\boldsymbol{\epsilon}(\mathbf{x},t)\,\mathrm{d}t.\end{aligned}$$

(2.8)

Here, $\boldsymbol{\epsilon}$ denotes the strain tensor and $\mathop{\mathrm{Tr}}(\boldsymbol{\epsilon})$ its trace. The colon stands for the Frobenius inner product. The kernels are defined with a negative sign, as the misfit is to be minimized and therefore the negative misfit gradient is used. The strain tensor $\boldsymbol{\epsilon}$ is calculated from the stress components used as variables in the simulation by inverting the isotropic stress-strain relation.

Corresponding misfit kernels for the density, $\rho$, P-wave velocity, $v_{\text{p}}$, and S-wave velocity, $v_{\text{s}}$ are given by

$$\begin{aligned}K^{\prime}_{\rho}(\mathbf{x})= & \leavevmode\nobreak\ K_{\rho}(\mathbf{x})+K_{\lambda}(\mathbf{x})+K_{\mu}(\mathbf{x}),\end{aligned}$$

$$\begin{aligned}K_{v_{\text{p}}}(\mathbf{x})= & \leavevmode\nobreak\ 2\rho(\mathbf{x})v_{\text{p}}(\mathbf{x})K_{\lambda}(\mathbf{x}),\end{aligned}$$

$$\begin{aligned}K_{v_{\text{s}}}(\mathbf{x})= & \leavevmode\nobreak\ 2\rho(\mathbf{x})v_{\text{s}}(\mathbf{x})(K_{\mu}(\mathbf{x})-2K_{\lambda}(\mathbf{x}))\,.\end{aligned}$$

(2.9)

So far, material properties and misfit kernels were defined as continuous functions of position in the subsurface. In order to make the inverse problem finite-dimensional, a discretization of these functions is required. The discretization by elements introduced in context with the forward simulation is used and the model $\mathbf{m}$ is now considered as a vector containing all values of the material properties in the elements. This implies constant values of the material parameters within the elements and it is possible to integrate the kernels over the elements. Hence, pre-integrated element-specific misfit kernels $\bar{K}_{\rho}^{k}$ are defined by Lamert [55] (explicitly given here for density)

$$\begin{aligned}\bar{K}_{\rho}^{k}=-\frac{\rho_{k}}{V_{k}}\int\limits_{D^{k}}\int\limits_{0}^{T}\mathbf{u}^{\dagger}(\mathbf{x},T-t)\cdot\partial^{2}_{t}\mathbf{u}(\mathbf{x},t)\,\mathrm{d}t\,\mathrm{d}V\,,\end{aligned}$$

(2.10)

where $D_{k}$ denotes element $k$, $V_{k}$ its volume and $\rho_{k}$ the value of density within this element.

As mentioned before, in the NDG method field variables at position $\mathbf{x}$ are expanded into Lagrange polynomials anchored at the nodal points. Hence, $\mathbf{u}^{\dagger}$ and $\mathbf{u}$ are expressed in the form

$$\begin{aligned}\mathbf{u}(\mathbf{x},t)=\sum\limits_{m=1}^{N_{\text{p}}}\mathbf{u}(\mathbf{x}_{m},t)l_{m}(\mathbf{x}),\ \mathbf{x}\in D^{k}\end{aligned}$$

(2.11)

with the Lagrange polynomials $l_{m}(\mathbf{x})$ and $N_{\text{p}}$ the number of nodal points. Inserting Eq. 2.11 into Eq. 2.10 and changing the order of volume and time integral results in

$$\begin{aligned}\bar{K}_{\rho}^{k}=-\frac{\rho_{k}}{V_{k}}\int\limits_{0}^{T}\sum\limits_{m=1}^{N_{\text{p}}}\mathbf{u}^{\dagger}(\mathbf{x}_{m},T-t)\sum\limits_{n=1}^{N_{\text{p}}}\partial^{2}_{t}\mathbf{u}(\mathbf{x}_{n},t)\int\limits_{D^{k}}l_{m}(\mathbf{x})l_{n}(\mathbf{x})\,\mathrm{d}V\,\mathrm{d}t.\end{aligned}$$

(2.12)

The volume integral on the right hand side is identical to the mass matrix used and computed in the NDG method,

$$\begin{aligned}M^{k}_{mn} & =\int\limits_{D_{k}}l_{m}^{k}(\mathbf{x})l_{n}^{k}(\mathbf{x})\,\mathrm{d}V\,.\end{aligned}$$

(2.13)

Since the elements from the NDG method are used as discretization for the inversion, the mass matrix is already known and the pre-integrated kernels (Eq. 2.12) become

$$\begin{aligned}\bar{K}_{\rho}^{k} & =-\frac{\rho_{k}}{V_{k}}\int\limits_{0}^{T}\sum\limits_{m=1}^{N_{\text{p}}}\mathbf{u}^{\dagger}(\mathbf{x}_{m},T-t)\sum\limits_{n=1}^{N_{\text{p}}}\partial^{2}_{t}\mathbf{u}(\mathbf{x}_{n},t)M^{k}_{mn}\,\mathrm{d}t\end{aligned}$$

$$\begin{aligned} & =-\frac{\rho_{k}}{V_{k}}\int\limits_{0}^{T}\mathbf{u}^{\dagger}(\mathbf{x}_{m},T-t)M^{k}_{mn}\partial^{2}_{t}\mathbf{u}(\mathbf{x}_{n},t)\,\mathrm{d}t\,.\end{aligned}$$

(2.14)

The element kernels $\bar{K}_{\lambda}$ and $\bar{K}_{\mu}$ are calculated in a similar way,

$$\displaystyle\begin{aligned}\displaystyle\bar{K}_{\lambda}^{k}&\displaystyle=-\frac{\lambda_{k}}{V_{k}}\int\limits_{0}^{T}(\mathop{\mathrm{Tr}}(\boldsymbol{\epsilon}^{\dagger}(\mathbf{x}_{m},T-t)))M^{k}_{mn}(\mathop{\mathrm{Tr}}(\boldsymbol{\epsilon}(\mathbf{x}_{n},t)))\,\mathrm{d}t,\\ \displaystyle\bar{K}_{\mu}^{k}&\displaystyle=-2\frac{\mu_{k}}{V_{k}}\int\limits_{0}^{T}\boldsymbol{\epsilon}^{\dagger}(\mathbf{x}_{m},T-t):(M^{k}_{mn}\boldsymbol{\epsilon}(\mathbf{x}_{n},t))\,\mathrm{d}t.\\ \displaystyle\end{aligned}$$

(2.15)

For $\bar{K}_{\mu}^{k}$ the sum over $n$ is applied to all components of $\boldsymbol{\epsilon}$ first and the inner product is to be calculated before applying the sum over $m$.

With this method, it is possible to calculate the misfit gradient without the use of an additional mesh. The values of $\mathbf{u}^{\dagger}$ and $\mathbf{u}$ at the nodal points $\mathbf{x}$ are directly given by the NDG method. Moreover, since the element size is typically about half a wave length due to computational stability, the resolution potential of FWI is conserved.

2.2.5 Inversion Procedure

Based on the gradients of the misfit function the L-BFGS (Low-memory Broyden-Fletcher-Goldfarb-Shanno) [81] method is applied to find a local minimum. The L-BFGS method uses models and misfit gradients of former inversion steps to approximate the Hessian $\mathbf{H}_{j}$ of inversion step $j$, thus boosting the convergence of search for a minimum to superlinear behavior. As proposed by [81] the approximation of the Hessian starts by defining $\mathbf{H}^{0}_{j}=\gamma_{j}I$ where $I$ is the identity matrix and $\gamma_{j}$ is a scalar which can be calculated from the model values and the misfit gradient of the latest inversion step. Afterwards, gradients and models from $L$ former inversion steps are used to iteratively approximate $\mathbf{H}_{j}$ based on $\mathbf{H}^{0}_{j}$.

The elastic properties of all elements contained in model $\mathbf{m}_{j}$ are updated in direction of the corrected gradient multiplied by a step length factor $\alpha_{j}$,

$$\begin{aligned}\mathbf{m}_{j+1}=\mathbf{m}_{j}-\alpha_{j}\mathbf{H}_{j}\mathbf{c}_{j}\,,\end{aligned}$$

(2.16)

where $\mathbf{c}_{j}$ is a vector composed of all the element-specific misfit kernels calculated in inversion step $j$. If $\mathbf{H}^{0}_{j}$ is chosen diagonal, $\mathbf{H}_{j}$ is diagonal as well and no matrix multiplication is needed to calculate $\mathbf{H}_{j}$. Thus, the multiplication of $\mathbf{H}_{j}$ and $\mathbf{c}_{j}$ reduces also to a simple multiplication for each entry of $\mathbf{c}_{j}$ instead of a matrix-vector multiplication ensuring fast computation of the model correction.

To determine $\alpha_{j}$, two trial step length $\alpha_{j,1}$ and $\alpha_{j,2}$ are chosen and a forward simulation is performed for both step length and the resulting waveforms are used to calculated the corresponding misfit. A second order polynomial, $\chi(\alpha_{j})$, is fitted to the misfit of the current model and the misfit for the two trial simulations. If existing, the minimum of the polynomial is taken as the optimal step length for the next iteration. In case the optimal step length is beyond the range of the trial step length, the maximum step length, $\alpha_{j,2}$, is doubled. If no minimum is found, the intermediate step length $\alpha_{j,1}$ is halved and the old value of $\alpha_{j,1}$ is used as $\alpha_{j,2}$. In both cases a further forward simulations is needed for the new step length. This procedure is repeated until a minimum $\alpha_{j,0}<\alpha_{\text{min}}\leq\alpha_{j,2}$ is found or until $\alpha_{j,1}$ or $\alpha_{j,2}$ reach a maximum or a minimum value, respectively.

The computational cost of the procedure described above requires one forward simulation for each seismic source to obtain the wave field for the current model, one forward simulation for the adjoint wave field and two forward simulations for the test step lengths. Due to an appropriate choice of $\gamma_{j}$ the test step lengths are not changed often. On average, 4-5 forward simulations per inversion step and per source are needed. Additional receivers do not increase the number of forward runs since the adjoint sources at the receiver positions can be fired at the same time. The presented method is most effective for a low number of sources and a high number of receivers within the observed region.

To ensure a stable and smooth convergence towards the minimum of the misfit function, a hierarchical multiscale approach is used. As suggested by several authors [12, 121, 73] the inversion starts with waveforms of low frequency content and higher frequencies are admitted gradually. In this way, large scale structures evolve at the beginning of the inversion which are gradually refined later as higher frequencies are added. Frequency content is controlled by low-pass filtering the observed waveforms and the source time function for the forward simulations in an identical way. This concept avoids the well-known cycle skipping problem where the phase difference between measured data and synthetic waveforms approaches one dominating signal period. Using low frequency content leads to a smoother misfit function making it more likely for the FWI procedure to converge to the global minimum. Adding higher frequencies gradually introduces additional detail in the model and ensures the convergence to at least a local minimum close to the global one. Without this approach, the inversion tends to converge into a shallow local minimum far away from the global one.

2.2.5.1 FWI in Two Dimensions

A common scenario during tunnel construction is the appearance of fractures in the rock mass in front of the drilling machine. In case of large scale fractures, the location of these fractures is often roughly known from geological surveys. Seismic waves interact with fractures and are partially reflected and partially transmitted at the fracture similar to a material contrast. Nevertheless, the dependency of transmission coefficient, reflection coefficient, and phase shift on the inclination angle differs strongly compared to a material contrast [86]. In this example we first generate synthetic waveforms for a fracture placed ahead of a tunnel interface and investigate the potential of locating the fracture using the inversion process. The synthetic waveforms are calculated using the 2D solver of nexd. The fracture is not directly modeled but described by an implementation of the Schoenbergs linear slip concept [104] by Möller & Friederich [72]. In this implementation, the response of the fracture is described by a characteristic frequency, $\nu$, that is calculated according to

$$\begin{aligned}\nu=\frac{Z_{1}+Z_{2}}{\eta Z_{1}Z_{2}}\,,\end{aligned}$$

(2.17)

where $Z_{i}$ are the impedances of the surrounding media and $\eta$ is the specific compliance, or the inverse of the specific stiffness, of the fracture [72]. According to [86] the reflection coefficient of a fracture is calculated by

$$\begin{aligned}R_{j}=\left|\frac{\text{i}\omega}{2\frac{\kappa_{j}}{\rho v_{j}}-\text{i}\omega}\right|,\quad j=\text{p},\text{s}\end{aligned}$$

(2.18)

where $\omega$ is the angular frequency of the incident wave, $\rho$ the density of the surrounding medium, $v_{j}$ is the P- or S-wave velocity and $\kappa=\frac{1}{\eta}$ is the specific stiffness of the fracture.

In this example, the reflective parameters of the fracture were chosen to emulate a material contrast, were the medium in front of the fracture (closer to the source) has a P-wave velocity of 3000 m/s and an S-wave velocity of 2000 m/s and the medium behind the fracture has a P-Wave velocity of 1600 m/s and an S-wave velocity of 1000 m/s. The density is identical in both media at 2200 kg/$\text{m}^{3}$. An inversion for this fault structure is discussed in detail by A. Lamert in [55] and [57] and will be referenced here for comparison.

Using the above parameters, reflection coefficients, $R_{\text{p}}=0.2$ and $R_{\text{s}}\approx 0.231$ are obtained for P- and S-waves respectively. Using these reflection coefficients, and a frequency of 500 Hz the specific stiffnesses for P-and S-wave are calculated as: $\kappa_{\text{p}}\approx$ 50.79 GPa/m and $\kappa_{\text{s}}\approx$ 23.31 GPa/m, leading to characteristic frequencies of the fracture

$$\begin{aligned}\nu_{\text{N}} & =15.4\,\text{kHz}\,,\end{aligned}$$

(2.19)

$$\begin{aligned}\nu_{\text{T}} & =13.2\,\text{kHz}\,.\end{aligned}$$

(2.20)

Figure 2.4 shows a comparison of the synthetic seismograms for the homogeneous background model without any reflectors and the seismograms calculated for two cases in which different reflectors were added. The first case shows the seismogram for a forward simulation were a fracture with the above parameters is added to the model (Fracture). The second case is a seismogram recorded at the same station in case of a fault (Fault). The seismograms are not identical due to the inherent difference of the reflectors used in the respective simulations. However, just by analyzing these seismograms, no assumption can be made whether the reflector is a fracture or a fault.

Fig. 2.4

Displacement seismogram of the horizontal component recorded at a surface receiver at the center of the simulation domain for the homogeneous model, the model incorporating a fault, and the model incorporating a fracture. The zoom-in panel highlights waves reflected by the fault or the fracture, respectively. The amount and amplitude of reflected waves is comparable for both cases but the seismograms are not equal due to the different phase shifts introduced by the different reflectors. ([55])

Fig. 2.5

Top: Homogeneous velocity model with fracture characterized by a red line (top row), inversion result after 276 iterations (center row), and inversion result for a fault with comparable reflection behavior like the fracture for comparison (bottom row). Bottom: Evolution of the misfit normalized to the misfit value of the starting model with full frequency content. Jumps correspond to an increase of the frequency content. ([55])

Figure 2.5 shows the model for the generation of the synthetic data and the results of the inversion for the fracture and for the fault. The fracture is best recovered in the P-wave velocity model as a thin low velocity zone almost at the exact position of the fracture in the initial mesh. It should be noted that a homogeneous velocity model with a fracture only defined at the element edges is used to produce the synthetic waveforms but during the inversion it is not possible to invert for the fractures itself. Instead the velocity values of the starting model are changed to represent the data and, thus, will produce an inhomogeneous velocity model without a fracture. The second observation from these results is that even though their parametrization is identical, the results from the inversion differ quite substantially.

From this data alone, no estimation of the true thickness of the fracture can be made, as the resolution of the fractures thickness highly depends on the frequency of the source wavelet. Nevertheless using these results, an operator will be able to determine if the reflector is a fracture or a fault and the location of either.

2.2.5.2 FWI in Three Dimensions

This example was originally published as part of the PhD thesis by A. Lamert [55].

To test the capabilities of the inversion procedure on three dimensional data, a synthetic test model is created with 100 m length in $x$ direction and 60 m length in both, $y$ and $z$ direction. A cylindrical tunnel with a diameter of 8 m and 21 m overburden extends 25 m into the medium parallel to the $x$-axis. The homogeneous background model has elastic properties of $v_{\text{p}}=3000$ m/s, $v_{\text{s}}=1700$ m/s, and $\rho=2000\,\text{kg/m}^{3}$ (see top row of Fig. 2.6). A spherical cave with a radius of 1.5 m is located 2 m above the tunnel line and 20 m in front of the tunnel as first inhomogeneity. The cave is modeled as a void with a free surface. A fault is located 46.5 m ahead of the tunnel where the seismic velocities change to $v_{\text{p}}$ = 2000 m/s and $v_{\text{s}}$ = 1100 m/s. The fault is rotated through 24.8° about the $y$-axis and afterwards through 20.5° about the $z$-axis. A seismic source is located centrally at the tunnel face pointing in the direction of $(1,0,1)$ to illuminate the ground with both, P- and S-waves. Receivers are placed at the free surface, the tunnel walls and the tunnel face to receive reflected waves as well as possible.

The starting model is a homogeneous model without the cave or the fault but with the tunnel. As elastic parameters, the bed rock properties around the tunnel are used. The mesh of this model consists of 65,747 elements and the simulation needs to be run for 8500 time steps (0.135 s simulation time) ensuring the observation of all reflected waves. With this, the simulation time for a single forward simulation is increased to almost 30 minutes compared to a couple of minutes for the 2D examples. However, the chosen size of the elements only allows to use a Ricker wavelet with a central frequency of 125 Hz leading to a spatial resolution 4 times smaller compared to the 2D examples. Increasing the frequency would lead to excessive computational times since the computational time grows with the fourth power of the frequency.

Fig. 2.6

Real model (top) and inversion result after 200 iterations from three different perspectives. All panels show the positions of the two obstacles: a fault illustrated as plane and a cavern illustrated as sphere. Velocity values close to the homogeneous background model are made transparent to show clouds of inhomogeneities. Receivers are represented by grey dots, the source at the tunnel face is shown in red. ([55])

The inversion starts with a cutoff frequency of 50 Hz increasing step wise to the maximum frequency of the Ricker wavelet during the inversion. Figure 2.6 shows the final inversion result after 200 iterations from different perspectives. The color scale is chosen such that a small band close to velocity values of the homogeneous starting model is completely transparent. From both edges of the transparent velocity band, the transparency decreases to the maximum and minimum values. Thus, clouds of higher and lower wave velocities compared to the bed rock become visible. The true position of the fault and the cave are also depicted in the inversion result by a plane and a sphere, respectively.

Compared to the 2D fault example presented in [55], many more small scale inhomogeneities are created but the fault is still clearly visible. The strongest signal of the fault is created on the left hand side of the tunnel axis for the P-wave velocity model (around the coordinate (0 m, 20 m, 0 m)) since waves from this area are directly reflected back to the receivers. The strongest signal for the S-wave velocity model appear at the top (around the coordinate (35 m, 0 m, 25 m)). With the velocity values increasing in front of the fault and decreasing behind it, a change at the fault from higher to lower wave velocities is obvious. However, determining the unknown velocity value behind the fault is only possible with high uncertainties since the reconstructed values vary strongly in the region where the fault is located. Additionally, the same effect as in the 2D example appears related to the distance between tunnel and fault. Due to the increase of the wave velocity in front of the tunnel, the fault plane is shifted to slightly higher distances from the tunnel. The lower part of the fault appears curved. This is probably caused by the fact that waves from here are mainly reflected to the receivers within the tunnel and only a small portion is recorded by receivers at the surface. Thus, considering only the receivers within the tunnel, a small aperture results. By using higher frequencies within the source signal, it can be expected that most of the small inhomogeneities will disappear and a clear picture of the fault is reconstructed similar to the 2D example. However, the provided computer would need several months for such a calculation.

The size of the cavern is chosen to be slightly higher than the shortest wavelength and is comparable to the size of the mesh elements as necessary for a stable simulation of the highest frequencies. Considering the inversion result for the P-wave velocity, the cavern appears as a small cloud with decreased wave velocity values not significantly smaller compared to the inhomogeneities around it. Within the S-wave velocity model a small cloud with clearly decreased velocity values can be seen with, however, almost the double radius as the real cave. The velocity values do not decrease to very small values and thus do not give a clear indication on the presence of a cavern in that area. Using a source signal containing higher frequencies would be necessary to obtain a clear picture with more reliable velocity values. However, the example clearly shows the potential of the FWI procedure to reconstruct large and small scale objects also in three dimensions. The problems of the computational effort can be expected to get less relevant in the future with increasing computer power.

2.2.6 Adjoint Frequency Domain Full Waveform Inversion

The wave modeling and the application of FWI is more illustrative in the time domain because an accurate selection of the considered period of time and an easy identification of emerging amplitudes in the seismic records is feasible. However, the non-linearity of the inversion is increased by this abundance of information. A separate analysis of single frequency groups by a frequency domain approach allows a mitigation of the non-linearity [1] by an intuitive application of a multi-scale approach where the used frequencies are gradually increased during the inversion scheme.

Frequency domain approaches of FWI have already been studied for other applications like the inversion of seismic records of a cross-hole experiment [85] or the inversion of tomographic seismic data of a physical scale model [84].

The complex-valued frequency domain elastic wave equation

$$\displaystyle-\omega^{2}\rho(\mathbf{x})\,\mathbf{u}(\mathbf{x},\omega)-\nabla\cdot\left(\mathsf{C}(\mathbf{x}):\nabla\mathbf{u}(\mathbf{x},\omega)\right)=\mathbf{f}(\mathbf{x},\omega)$$

(2.21)

is obtained by a Fourier transformation of the time domain’s counterpart in Eq. 2.2. The complex-valued wave field $\mathbf{u}(\mathbf{x},\omega)$ can be solved for an angular frequency $\omega$ and the complex-valued excitation force $\mathbf{f}(\mathbf{x},\omega)$.

An application of numerical schemes to solve Eq. 2.21 leads to a linear system of equations. Therefore, the initial factorization of the system matrix enables the computation of additional wave fields of the current ground model and the same angular frequency for other source excitations by a comparatively low increase of the computational effort. This makes the frequency domain approach favorable in terms of computational efficiency for applications with a high number of sources.

In time domain modeling, an increase of the discretization level of the ground model for modeling higher frequencies brings a need for a decrease of the time increment to ensure numerical stability. This dilemma is avoided by frequency domain modeling and therefore, the choice of the applied numerical scheme is not limited by this problem. Nevertheless, finite element approaches are favorable because the Neumann boundary condition at the free surfaces, which acts as reflecting surfaces, of the Earth’s surface as well as of the tunnel walls are fulfilled implicitly.

A major drawback of the frequency domain modeling is that the artificial borders of the considered computational domain have to be treated very carefully. If no high attenuation effects occur within the subsurface domain, the reflections from the artificial borders contaminate the whole wave field. In time domain modeling only the later points in time are affected by these reflections which can be simply neglected by a reduction of the considered time interval.

An efficient way to suppress these erroneous reflections is an application of small absorbing boundary layers at the artificial borders of the computational domain. The so-called perfectly matched layer method enables a smooth absorption of escaping waves by a coordinate stretching into the imaginary plane [9]. For shallow subsurface models like in the considered tunnel models, an application of convolutional perfectly matched layers is recommended [25].

The frequency domain Green’s functions $\mathbf{g}(\mathbf{x},\omega)$, which are the system response to an impulse excitation, are illustrated in a shallow two-dimensional tunnel environment for excitation by a horizontal single force which is located at the front tunnel face in Fig. 2.7 for a frequency of 500 Hz. An absorption of the elastic waves within the perfectly matched layers (dashed regions) is observed. Even though a homogeneous ground model was used, it is not recognizable by the wave field whether there is a disturbance in front of the tunnel face or not.

Fig. 2.7

Real part of the Green’s functions $\operatorname{Re}(\mathbf{g})$ in $x$- (left) and $y$-direction (right) in a two-dimensional tunnel environment for a frequency of 500 Hz. Free surfaces are located at the Earth’s surface and around the tunnel. The origins of the perfectly matched layers are indicated by the dashed lines. The illustrated ground model has a homogeneous P-wave velocity $v_{\text{p}}=3800$ m/s, S-wave velocity $v_{\text{s}}=2200$ m/s and density $\rho=2400$ kg/m${}^{3}$. The applied source is a horizontal single force

Since the wave field is only solved for a limited number of currently investigated frequencies of the $i^{\text{th}}$ frequency group the proposed misfit function of Eq. 2.3 is adapted to

$$\displaystyle\chi_{i}(\mathbf{m})=\sum_{f=1}^{F_{i}}\sum_{s=1}^{N_{\text{s}}}\sum_{r=1}^{N_{\text{r}}}\,\,\left(u_{r}^{s}(\omega_{f};\mathbf{m})-\bar{u}_{r}^{s}(\omega_{f})\right)\left(u_{r}^{s}(\omega_{f};\mathbf{m})-\bar{u}_{r}^{s}(\omega_{f})\right)^{\ast}.$$

(2.22)

The number of frequencies within the current frequency group is denoted by $F_{i}$ whereas $(\cdot)^{\ast}$ is the complex conjugate. The complex displacements of the reference seismic records $\bar{u}_{r}^{s}(\omega_{f})$ are calculated by a discrete Fourier transformation. A preservation of low frequency features is guaranteed by combining the increasing frequencies with low frequencies from former iteration steps.

The discrete adjoint gradient of the misfit function is calculated by differentiating the misfit in Eq. 2.22 with respect to the discretized material properties (e.g. discretized within single elements or at every node). For computing the gradient, the product rule has to be applied and the derivative of the displacement with respect to the discretized material properties is evaluated by using the according derivative of numerical representation of Eq. 2.21. The resulting system of equations can be simplified by calculating the adjoint wave field by using the negative derivative of the misfit function with respect to the displacements at the receiver stations as adjoint source [26]. The computation of the adjoint wave field in the frequency domain only needs low additional computational effort since the already factorized system matrix can be reused again.

For minimizing Eq. 2.22 by changing the material properties of the current ground model different techniques as steepest descent method, conjugate gradient method or the L-BFGS method [81] can be applied to find a suitable search direction. The step length can be evaluated by heuristic schemes or by e.g. calculating the minimum of a quadratic approximation of the misfit function with three points [107]. Singularities occur for the wave field at the sources as well as for the adjoint wave field at the receivers. Therefore, the gradient has disproportionately high changes at these positions [83] and makes an exploration of the ground in front of the tunnel more difficult. By a preconditioning of the gradient, e.g. setting the gradient equal to zero around the sources and receivers, the negative impact of this effect on the inversion scheme might be reduced.

A deconvolution of the source function into a spatially dependent impulse part $\boldsymbol{\delta}(\mathbf{x}-\mathbf{s})$, which is equal to zero everywhere except at the considered source position $\mathbf{s}$, and a frequency dependent part $h(\omega)$ is in the frequency domain straightforward,

$$\displaystyle\mathbf{f}(\mathbf{x}-\mathbf{s},\omega)=h(\omega)\,\boldsymbol{\delta}(\mathbf{x}-\mathbf{s}).$$

(2.23)

By neglecting the frequency dependent part $h(\omega)$ for the forward wave modeling, the Green’s functions $\mathbf{g}(\mathbf{x},\omega)$ are calculated. The displacement at the receiver station can be calculated with the Green’s functions by a convolution with the frequency dependent source function

$$\displaystyle u_{r}^{s}(\omega_{f};\mathbf{m})=h^{s}(\omega_{f})\,g_{r}^{s}(\omega_{f};\mathbf{m}).$$

(2.24)

Under the assumption that the transfer function between the ground and a receiver $r$ is approximately equal for all receivers $N_{\text{r}}$, a simultaneous approximation of the source signatures during every iteration of the inversion is possible. By setting the derivative of Eq. 2.22 with respect to the source function $h^{s}(\omega)$ equal to zero to satisfy the necessary condition for a minimum [84], the source function is approximated by

$$\displaystyle h^{s}(\omega_{f})=\frac{\sum_{r=1}^{N_{\text{r}}}\left(g_{r}^{s}(\omega_{f};\mathbf{m})\right)^{\ast}\,\bar{u}_{r}^{s}(\omega_{f})}{\sum_{r=1}^{N_{\text{r}}}\left(g_{r}^{s}(\omega_{f};\mathbf{m})\right)^{\ast}\,g_{r}^{s}(\omega_{f};\mathbf{m})}.$$

(2.25)

The calculated source function depends on the current ground model $\mathbf{m}$. Therefore, the source function is approximated for every iteration of a frequency group. Since the calculation of the displacements is with Eq. 2.24 only a linear operation, the already calculated Green’s functions can be reused and no additional forward simulations are performed.

If the assumptions made are valid, the frequency domain approach enables an inversion scheme in which no information of the source signature is needed in advance. This might be a great advantage since a prior estimation of the source function is cumbersome.

Fig. 2.8

Results of a full waveform inversion with a frequency domain model for a two-dimensional tunnel environment with a different number and position of sources (triangles) and receivers (squares). The P-wave velocity distribution is on the left side and the S-wave velocity distribution is illustrated on the right side. In the first row the wave velocity distribution of the reference model is illustrated. The shapes of the three disturbances are indicated within the inversion results

In Fig. 2.8, the inversion results for a two-dimensional tunnel environment are illustrated, where different numbers and locations of sources and receivers are used. The resulting P-wave velocity $v_{\text{p}}$ is shown on the left side and the S-wave velocity $v_{\text{s}}$ on the right side. The ambient P-wave velocity is $v_{\text{p}}=3800$ m/s and the ambient S-wave velocity is $v_{\text{s}}=2200$ m/s, whereas the density is $\rho=2400$ kg$/$m${}^{3}$ and is assumed to be constant. The reference ground model, which is illustrated on top of Fig. 2.8, contains three disturbances in front of the tunnel track with different shapes and elastic properties. Free surfaces are applied at the Earth’s surface and at the tunnel, whereas the absorbing boundary layers are illustrated by the dashed regions.

For the computation of the wave fields, a finite element approach is used, where hierarchical higher-order shape functions [108] are employed for efficiently increasing the accuracy of the numerical scheme for higher frequencies (which lead to shorter wavelengths) by just adding additional shape functions without changing the initial mesh. For the illustrated application, the ground properties are discretized in the nodes. The used synthetic reference displacements are calculated with the same approach in advance to the several frequency groups. As reference source functions $\bar{h}^{s}$ Ricker wavelets with a peak frequency of 500 Hz, without a time delay and a scaling factor of $10^{6}$ are used. A simultaneous approximation of the source function by Eq. 2.25 is applied for all results in Fig. 2.8. For the first eight frequency groups only one frequency is employed. The other thirty frequency groups contain a combination of an increased frequency and a lower frequency. The inversion is performed by using 12 iterations for each frequency group. For all four examples, the displacements in both spatial directions are measured at the indicated receivers.

The used source and receiver configuration of the first example (second row of Fig. 2.8) is likely to be used for today’s exploration approaches in mechanized tunneling. Only one source is positioned in the middle of the tunnel face and the receivers are located at the tunnel face as well as at the tunnel walls. The resulting wave velocities allow only a prediction of the position of the first disturbance but neither its shape nor its actual elastic properties are quantifiable accurately. Furthermore, spurious fluctuations of the wave velocities occur which make an unambiguous prediction difficult. For the second example (third row of Fig. 2.8), a source is added at the Earth’s surface 55 m in front of the tunnel. Therefore, not only reflected waves are analyzed but also directly refracted waves of the second source are captured. The position of all three disturbances are hinted by the resulting wave velocities, especially by the S-wave velocity. However, only the shapes and properties of the first two disturbances can be predicted by the S-wave velocity. For the third example (fourth row of Fig. 2.8), only nine evenly distributed receivers are added at the Earth’s surface in comparison to the first example. The resulting wave velocities enable a good prediction of the position and the properties of all three disturbances whereas only the shape of the first two obstacles are predictable in an accurate way. A rapid increase followed by a sudden decrease of the wave velocities occur at the borders of the third disturbance, which produces a comparable reflection behavior since the gradient of the ground properties is nearly the same as the gradient of the reference ground model. This ambiguity of the seismic records has to be taken into account for evaluating the results of the full waveform inversion. The fourth example (fifth row of Fig. 2.8) combines the additional source of the second example as well as the additional receivers of the third example. An accurate prediction of the position, shape and properties of the disturbances is enabled on the basis of the inversion results.

It is observed that adding sources and receivers at the Earth’s surface improves the prediction of geological changes in front of the tunnel face. The application of sources and receivers at the Earth’s surface may not be possible in urban areas due to restrictions on the access to the surface. However, as illustrated by the first example, a prediction of the first reflection feature in front of the tunnel is already possible by only using sources and receivers at the tunnel.

As already announced, a simultaneous approximation of the source signature was used. A comparison of the real part of the reference and the approximated source signature of the first example is illustrated in Fig. 2.9. Only the reference and the approximated value of the highest frequency of the frequency groups is displayed.

Fig. 2.9

The change of the real part of reference $\bar{h}^{s}$ and approximated source signature $h^{s}$ for the highest frequency of a frequency group $\omega_{f,\text{max}}$ of the first full waveform inversion example (second row of Fig. 2.8) during the several iterations is displayed

A sufficient approximation of the source function is obtained which enables a full waveform inversion scheme without prior knowledge of the source signature.

Since the curvature of the tunnel as well as other effects are not considered by a two-dimensional model, more realistic examples have to be investigated by using three-dimensional tunnel models. Therefore, the proposed inversion scheme is tested on a shallow tunnel domain where the reference ground model includes a spherical disturbance in front of the tunnel track. The ambient wave velocities are $v_{\text{p}}$ = 4000 m/s and $v_{\text{s}}$ = 2400 m/s, whereas the properties of the sphere are $v_{\text{p},\text{sphere}}$ = 2800 m/s and $v_{\text{s},\text{sphere}}$ = 1700 m/s. The density is assumed to be constant with $\rho$ = 2500 m/s. The tunnel has a diameter of 8 m and its center is located 18 m below the Earth’s surface. The sphere has a radius of 8 m and its center is on the level of the tunnel’s center with a distance of 25 m to the front tunnel face. The FWI is started again with an homogeneous ground model.

Since the computation demand for the inversion schemes is still very high for three-dimensional problems, only 16 freqeuency groups are used where the first nine groups contain only single frequencies and the other seven groups combine two frequencies within a group. The frequencies are only increased to $f$ = 381.97 Hz because the wave field becomes more complex for higher frequencies and therefore a higher discretization would be needed. But for the used disturbance size this frequency range is sufficient.

The full waveform inversion is performed for two different configurations of sources and receivers. The first configuration only employs a source in orthogonal direction at the center of the tunnel face as well as only receivers at the tunnel face and walls. The second configuration uses additional sources and receivers at the Earth’s surface. The receivers record the displacements in all three spatial directions. All sources use a Ricker wavelet with a peak frequency of 500 Hz, without a time delay and a scaling factor of $10^{6}$. The resulting wave velocity distributions are illustrated in Fig. 2.10, where the source and receiver positions as well as the position of the disturbance are indicated, too.

Fig. 2.10

P-wave velocity $v_{\text{p}}$ (left) and S-wave velocity $v_{\text{s}}$ distribution (right) of the full waveform inversion results of a three-dimensional shallow tunnel domain for two different configurations of sources (red spheres) and receivers (blue spheres). The position of the spherical disturbance of the reference model is indicated by grid lines

For the first source-receiver configuration, the S-wave velocity field allows a prediction of the front face of the sphere, whereas the P-wave velocity field only provides spurious fluctuations directly in front of the area where the gradient is preconditioned (around the sources and receivers). Nevertheless, these results allow the guess that a disturbance with decreased wave velocities might be in front of the tunnel. The second source-receiver configuration leads to improved inversion results. The S-wave velocity distribution gives an accurate representation of the the position, shape and S-wave velocity of the sphere. Whereas the P-wave velocity field only gives a blurred image of the sphere but its position and the trend of the P-wave velocity are identifiable. An application of additional frequency groups containing higher frequencies would improve the representation of the sphere by the reconstructed P-wave velocity field. Therefore, these results would allow a more precise prediction of the disturbance.

The three-dimensional results demonstrate that the two-dimensional results give good insights into the influence of the different source-receiver configurations as well as that seismic reconnaissance via full waveform inversion by an adjoint frequency domain approach provides promising results for synthetic seismic records.

2.2.7 Validation with Small-Scale Laser Experiment

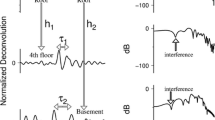
In order to validate the FWI methods with real data, a small-scale laser experiment is set up with which ultrasonic measurement can be acquired. The validation with ultrasonic data brings a significant gain compared to the validation with synthetically generated data since noise as well as measurement errors are naturally included. Furthermore, also modeling errors occur when setting up the forward model. All of these error types also occur during field scenarios, but not in synthetic tests, and therefore, the robustness of the FWI methods against these error types can be tested with the laboratory data. Rich field data is difficult to get, while in the small-scale experiment, a broad variety of scenarios can be tested in order to prepare the methods for a later in-situ application. A picture of the experiment with labeled components is provided in Fig. 2.11, while a sketch of the measurement chain of the experiment is illustrated in Fig. 2.12.

Fig. 2.11

Picture of the experiment with labeled components

Fig. 2.12

Measurement chain of the experiment

On the computer, the source signal is specified which is forwarded to a function generator and then to a power amplifier. Arriving at the ultrasonic transducer, the electrical signal is converted into a mechanical waveform. The transducer applies a force onto the specimen and thus initiates a seismic wave which propagates through the specimen. A laser interferometer enables the contactless recording of seismic data, where a positioning system allows the measurement at various points along predefined lines or areas. The recorded signal is forwarded to the computer for data acquisition. In order to minimize vibrational influences from the environment, the setup is placed on an optical table.

Intensive preliminary investigations are conducted with the aim to maximize the repeatability of measurements as well as their signal-to-noise ratios [114]. Firstly, it is found out that a stacking of single measurements is necessary in order to achieve a repeatable high-quality signal, where a minimum of 100 stacked measurements is recommended. Secondly, it is shown that the attachment of aluminum tape on the specimen’s surface when measuring on porous material is highly beneficial in order to improve the reflection of the laser signal. With these methods, a signal-to-noise ratio of 4322 (or 36.4 dB) could be achieved for 100 stacked measurements acquired on a concrete specimen with aluminum tape, where the signal-to-noise ratio of a single measurement without aluminum tape amounted to 11.3 (or 10.6 dB) only.

2.2.7.1 Hole Imaging in an Aluminum Block

First validation of the methods is performed with ultrasonic data acquired on an aluminum block which contains a drilling hole. Since a consideration of homogeneity and isotropy is most widely valid for aluminum, simulation results may be expected to be closer to the measurement than for rock materials. Therefore, modeling strategies such as the estimation of the material properties and the transducer’s source function can be more easily developed. More information on the experiment, the forward modeling and UHSA may be found in [114, 117]; more information on the time domain adjoint solution may be found in [55].

Fig. 2.13

Aluminum block with a drilling hole. a Photo of measurement setup, b illustration with measurement configuration. The shape of the transducer is illustrated in red. Points of laser measurements are visualized by the green dots

The aluminum block with its drilling hole is shown in Fig. 2.13 with a photo of the measurement setup in Fig. 2.13, left, and an illustration in Fig. 2.13, right. A coordinate system is placed at the center of mass of the ideal block as shown in Fig. 2.13, right. The outer dimension of the aluminum block is 200.4 mm $\times$ 103 mm $\times$ 100 mm, where a hole of 16 mm diameter is drilled throughout the $y$-dimension at $(-10,y,20)$ mm. The green dots illustrate the points of laser measurement, the red cylinder visualizes the shape of the ultrasonic transducer. The source function which is sent to the transducer is a Ricker wavelet with a central frequency of 300 kHz. In order to determine the material properties of the specimen and the transducer’s source function, a second undisturbed aluminum block with the same outer dimensions as above is used, which is illustrated in Fig. 2.14 (analogous to the illustration in Fig. 2.13). Here, only a single measurement is acquired on the opposite site of the transducer as illustrated. At all of the above-mentioned points of measurement, 200 single measurements are stacked in order to increase the signal qualities. Offsets of the records are removed by subtraction of average amplitudes before signal arrival. Bandpass filters with cutoff frequencies of 50 and 800 kHz are applied to each trace.

Fig. 2.14

Undisturbed aluminum block. a Photo of measurement setup, b illustration with measurement configuration. The shape of the transducer is illustrated in red. The single measurement is visualized by the green dot

Before an inversion scenario can be set up, a forward model needs to be constructed. In order to estimate the material properties and the transducer’s source signature, a model corresponding to the setup shown in Fig. 2.14 is set up. Dimensions are carefully measured and a brick is modeled and meshed, where all surfaces are defined as free boundaries. The material behavior is assumed to be elastic and therefore, material properties reduce to density $\rho$, compressional wave velocity $v_{\text{p}}$, and shear wave velocity $v_{\text{s}}$. Density $\rho$ is determined and implemented into the model. With the spectral-element code specfem3D [50], numerical solutions to various gridded combinations of $v_{\text{p}}$ and $v_{\text{s}}$ are computed, where an ideal Ricker is used as source function. By incorporation of the acquired measurement, the misfit functionals are determined and the wave velocity combination corresponding to the smallest misfit value is picked, which is $v_{\text{p}}$ = 6340 m/s and $v_{\text{s}}$ = 3110 m/s. In a next step, the transducer’s source function is estimated. If it is assumed that the numerical model captures all properties of the experimental model (e.g. in terms of geometry and material properties), the source function in frequency domain $R_{\text{exp}}(\omega)$ can be estimated as [117]

$$\displaystyle R_{\text{exp}}(\omega)=\frac{S_{\text{exp}}(\omega)}{S_{\text{syn}}(\omega)}\cdot R_{\text{syn}}(\omega),$$

(2.26)

where $R_{\text{syn}}(\omega)$ is the ideal (Ricker) source function, $S_{\text{exp}}(\omega)$ the acquired waveform, and $S_{\text{syn}}(\omega)$ the simulated waveform in frequency domain for the angular frequency $\omega$.

Fig. 2.15

Ideal Ricker source function and estimated source function. The waveforms are normalized with their second local extremum

Fig. 2.16

Visualization of the acquired measurement, the synthetic response to an ideal Ricker source function, and the synthetic response to the estimated source signature shown in Fig. 2.15. The waveforms are normalized with their second local extremum

Figure 2.15 shows the estimated source function after transformation to time domain compared to the ideal Ricker source function. With the estimated waveform as source function, a new simulation is set up, where the outcoming waveform is plotted in Fig. 2.16 (green), together with the measurement (black) and the simulated wavelet generated with the ideal Ricker (gray dotted). It becomes visible that the waveform agreement to the measurement improves substantially compared to the prior estimation. The high correlation is a sign for well-fitting material properties and a well-estimated source signature, forming the basis for the upcoming inversion scenarios.

UHSA inversion

In this section, UHSA is applied to the measurement data (setup shown in Fig. 2.13), where the previously determined material properties and the estimated source signature are used. Since UHSA is based on the implementation of prior knowledge, a parametrization needs to be derived. Here, it is selected to consist of just two center coordinates $(x,z)$ respective to the coordinate system in Fig. 2.13, right, where the corresponding drilling spreads all over the specimen in $y$-direction. The diameter of the drilling is considered to be known which has the advantage that with this kind of parametrization with only two parameters, a relatively fast computation and a visualization of the misfit functional is possible. The time window of investigation is set to $8.8\times 10^{-5}$ s since according to Fig. 2.16, a high agreement of experimental and synthetic waveforms is observed during this time. In a first step, a misfit landscape is computed by linear interpolation of 1024 sampled parameter configurations and visualized in Fig. 2.17.

Fig. 2.17

Course of UHSA on the misfit landscape, where a certain location on the map specifies position $(x,z)$ of the hole in the computational model. The color corresponds to the respective misfit functional

The abscissa corresponds to the $x$-axis in Fig. 2.13, while the ordinate corresponds to the $z$-axis. Several local minima are visible; however, there is a distinct global minimum around the actual center of the boring at $(x,z)=(-10,20)$ mm. UHSA is set up for 40 cycles, where the course of the algorithm is drawn onto the misfit landscape in Fig. 2.17. It is visible that the SA algorithm rather accepts parameter configurations with smaller misfit functionals as many SA samples lying in the red regions are rejected. If a SA proposal is accepted, the UKF samples different parameter configurations with the aim to move into the direction of the neighboring local minimum, which succeeds in most cases. The global minimum region is intensively explored and the parameter configuration with the lowest misfit functional is found at $(x,z)=(-8.86,19.17)$ mm, which is close to the actual expected global minimum. The entire inversion requires 460 forward simulations within 55 hours of computation time on a 26-core computer with 2.4 GHz each and 96 GB RAM.

Time domain adjoint inversion

In this section, the results for an inversion scenario using the adjoint time domain FWI on the setup shown in Fig. 2.13 are presented. The initial model is a homogeneous model described by the material parameters determined above. The source time function used here is the green curve shown in Fig. 2.15. The computational mesh consists of 285,588 tetrahedral elements. The computation time for one single simulation on a machine with two Intel Xeon E5-2698 v4 processors with 20 cores each and 256 GB RAM on 40 threads is approximately 1.35 hours.

Fig. 2.18

Inversion results of the P-wave velocity model in the left column and the S-wave velocity model in the right column from three different perspectives for the inversion changing both P- and S-wave velocities. Grey dots represent seismic stations and black dots the seismic source. ([55])

A comparison of the measured seismograms to synthetic ones showed large discrepancies for the receivers closest to the source. Consequently, only the 20 receivers farthest away from the source were used in the inversion process (see [55]). Figure 2.18 shows the inversion results, where the changes in P- and S-wave velocities are shown in three perspectives. Around the position of the drilling, a decrease of the P-wave velocity is visible. In addition, a number of other regions with altered wave velocities are observed, where possible reasons are described in [55]. For the S-wave model, on the other hand, an increase in velocity at the position of the drilling is observed. In [55], Lamert provides a detailed analysis as to why an increase rather than a decrease is observed in this instance. Using both velocity models, an inhomogeneity is identified in the vicinity of the true position of the drilling. The center is estimated by [55] at $(x,z)=(-15.5\,\text{mm},24.5\,\text{mm})$ with a radius of 6.5 mm, while the true center lies at $(x,z)=(-10.0\,\text{mm},20.0\,\text{mm})$ with a radius of 8.0 mm.

2.2.7.2 Layer Change Imaging in a Concrete Block

In this section, an experimental model with certain similarities to field models is used to acquire ultrasonic data with which UHSA and UKF-PaLS are validated. For more information, readers are referred to [114, 115]. The experimental model is shown in Fig. 2.19 with a photo in Fig. 2.19, left, and an illustration of the inner structure in Fig. 2.19, right.

Fig. 2.19

Concrete block with measurement configuration. Dimensions in m. Sources in red, locations of laser measurement in green. Left: Photo of the specimen. Right: Illustration of the ideal inner structure with two materials in different colors

The specimen is a concrete block which has a relatively large dimension in $y$-direction compared to the other directions, enabling thus to perform the upcoming simulations in 2D instead of in 3D for the gain of a reduced computation time. Into the block, a linear material change is incorporated, where the two materials are composed of different concrete mixtures. In order to illustrate a 2D tunnel geometry in the later simulation model, the block has a material recess at $x=0$. For the acquisition of the ultrasonic data, two source locations are specified which are illustrated by the red dots. At each source location, two source signals are released in the form of tone burst signals centered at 80 and 100 kHz. For each source signal, data is acquired at 532 receiver points, where the locations of the laser measurements are illustrated by the green lines. In order to improve the laser reflection, aluminum tape is attached along the lines of measurement. At each point of measurement, 100 single measurements are stacked. Bandpass filters with cutoff frequencies of 10 kHz and 150 kHz are applied to each record. A $\sqrt{t}$-filter is applied to the measurement data in order to approximately convert the amplitudes from the 3D spreading to a 2D spreading as for instance performed in [85].

Same as in the previous section, a forward model is to be constructed, where the main tasks are the determination of the background material properties and the estimation of the source signal. For their estimation, only the receivers between $x=0.1$ m and $x=0.16$ m are used within a reduced time window in order to minimize the impact resulting from the disturbance. Afterwards, a homogeneous model is set up with the outer dimensions of Fig. 2.19, right. The geometry and the mesh are defined, where again all boundaries obtain free boundary conditions. Simulations are conducted with the spectral-element code specfem2D [118]. The density is determined and implemented into the model. Afterwards, material properties are determined in the same way as explained in Sect. 2.2.7.1, where also attenuation is included. However, the misfit functionals increase for increasing attenuation and thus, elastic material behavior without attenuation is considered for inversion. Disturbance material properties are determined in a similar way like the background material properties, where the material properties for both domains are shown in Fig. 2.19, right. First estimations of the source functions are determined by a direct measurement with a second transducer at the head of the first transducer. Afterwards, the source signal is improved same as in the previous section by applying the relation Eq. 2.26 at a reference receiver. For inversion, the receiver signals are cut in such a way that no reflections arrive from the boundaries of the experimental model Fig. 2.19, left, in positive and negative $y$-direction. The density is assumed to be constant all over the model domain.

UHSA inversion.

Prior to inversion, a parametrization is set, which is visualized in Fig. 2.20. It is composed of a linear connection of a top border position $x_{\text{t}}$ at $z=0$ with a bottom border position $x_{\text{b}}$ at $z=0.25$ m, a disturbance wave velocity $v_{\text{p,d}}$ and a Poisson’s ratio $\nu_{\text{d}}$.

Fig. 2.20

Parametrization and determined geometry for configuration 1 (red) and configuration 2 (blue)

Two source-receiver configurations are tested, where the first configuration includes all receivers along the green lines in Fig. 2.19, right, and where the second configuration includes the receivers only at the top surface $z=0$. The inversion results are shown in Table 2.1 and a visualization of the determined geometry as well as of the source-receiver configurations is given in Fig. 2.20 for configuration 1 (red) and configuration 2 (blue). It is observed that for both configurations, the determined values are very close to the expected true values. For configuration 2, $x_{\text{b}}$ is determined a little less precise since receivers only occur at the top surface. The inversion scenarios took about 12 hours on a 26-core computer with 2.4 GHz each and 96 GB RAM, where 3762 (configuration 1) or 3933 (configuration 2) forward simulations were required.

Tab. 2.1 Inversion results of UHSA: expected true value and inversion results

UKF-PaLS inversion

The initial model for UKF-PaLS is set up with 216 bumps and visualized in Fig. 2.21, where analogous to Fig. 2.2, an uncertainty measure is plotted. Same as UHSA, UKF-PaLS is validated with the two source-receiver configurations described in the previous paragraph. Figure 2.22 shows the inversion results for both configurations after 20 iterations compared to the expected true geometry illustrated by black dashed lines. It is observed that for both configurations, most of the bumps outside the region of the actual disturbance domain vanish while parts of the disturbance become visible. The uncertainty measure correctly extends the region of the actual disturbance. However, there a still errors which mainly occur due to measurement errors, noises and modeling errors. At height of the tunnel, the disturbance is determined quite precisely for both configurations, which would be most important for an application during mechanized tunneling. Both computations require about 12 hours on a 26-core computer with 2.4 GHz each and 96 GB RAM, where 17360 forward simulations are consumed.

Fig. 2.21

Initial model. The uncertainty measure introduced in Sect. 2.2.3.2 is plotted in medium dark gray

Fig. 2.22

Inversion results after 20 iterations for receiver configuration 1 (left) and receiver configuration 2 (right). The expected true geometry is illustrated by black dashed lines

In summary, both UHSA and UKF-PaLS can determine the inner structure of the concrete block satisfactorily. With the dimensionality reduction applied in UHSA, results are even close to exact. Primarily due to model side reflections which would not occur in a real tunneling model and due to source-receiver configurations, the findings cannot fully be compared with field scenarios. However, the experiment brings similarities enabling a validation with a certain relation to mechanized tunneling.

2.2.8 Summary and Outlook

After the explanation of the principle of seismic reconnaissance in general, state-of-the-art methods for application during mechanized tunneling are shortly presented. Changes for the better are identified, directly leading to the field of full waveform inversion with which a more detailed representation of the subsoil can be achieved. Four different FWI approaches are introduced, that are two Bayesian FWI approaches, one adjoint FWI approach in time domain, and one adjoint FWI approach in frequency domain. Synthetic inversion scenarios are created, where all of the methods are generally able to image the anomalies in a tunnel environment. For the validation of the FWI methods with real data, a small-scale laser experiment is set up with which ultrasonic data is created. Since noise, measurement errors and later modeling errors occur, the grade of validation is evaluated to be high. Two experiments are presented, where the tested inversion methods show a certain robustness against these kinds of errors, being able to reconstruct the anomalies which are incorporated into the specimen. The results give a hint that the methods are generally applicable for exploration during mechanized tunneling. However, it is to mention that the methods are still far from delivering results close to real-time or within a time which would be necessary for an application during mechanized tunneling. Nonetheless, with exponentially growing computational power, full waveform inversion may become applicable in the future.

2.3 System and Parameter Identification Methods for Ground Models in Mechanized Tunneling

Collecting data of excavation-induced changes on surroundings in a linear project like tunneling may enable the engineers to adapt the computational model for subsequent phases through back analysis and reduce uncertainty, subsequently. In this regard, sensitivity analysis methods play a crucial role in selecting the most pertinent input components that must be adjusted using available experimental or field data. The suggested conceptual approach aims to increase the efficiency of measurement-based system identification in mechanized tunneling by using various mathematical approaches such as optimization based back analysis, and optimum experimental design.

2.3.1 Back Analysis

Over the last decade, there has been a growth in the use of numerical models for predicting ground behavior, surface settlements, and the loading and deformation of tunnel linings. The rising power and efficiency of current computer technology, as well as significant advances in computational mechanics, have fueled the development of more complicated numerical models with more characteristics.

In the numerical simulation of mechanized tunneling, more or less severe idealizations are frequently used, such as modeling its stress-strain behavior using a simplified constitutive law or initial boundaries, assuming simplified hydro-mechanical initial boundaries in the subsoil, or a homogenization of soil mass. The epistemic uncertainties that arise as a result of such models may result in either a conservative design or a significant risk of instability. Back analysis techniques are commonly adopted in geotechnical applications to calibrate constitutive parameters for numerical simulation models. For large-scale geotechnical applications where the region of the impacted ground is considerably larger than the tested samples, a calibration technique based on existing measurements is required for an effective evaluation of the soil characteristics.

The observed excavation-induced changes in the measurement logs (ground displacements, stresses, pore water pressures, etc.) will be utilized to update the computational model in this regard through system adaptation. If the observations show that the design values are not being followed, the back analysis may be used to determine realistic soil properties and system performance without the need for additional field surveys. With the significant development of computer technology and advanced algorithms, the concept of back analysis via in-situ measurement can be implemented by an optimization procedure, as illustrated in Fig. 2.23.

Fig. 2.23

The applied iterative approach via back analysis, from [59]

Observations or measurements $\mathbf{\tilde{y}}$ are compared to model outputs $\mathbf{y}$ obtained from initial assumptions on model parameters $\mathbf{m}$. To reduce the discrepancy between measurement and model response, the model parameters are varied. In the end this corresponds to the formulation of the objective function. The complexity of this problem emerges from the circumstance that there are usually several model parameters that are correlated with each other and that the system behavior is non-linear, explicitly in the considered geotechnical applications. Therefore, finding that optimal parameter combination $\mathbf{\hat{m}}$ that causes the minimum discrepancy between measurement and model response requires so-called optimization algorithms as described in Sect. 2.3.4.

The aforementioned discrepancy between measurements $\mathbf{\tilde{y}}$ and model responses $\mathbf{y}(\mathbf{m})$ is usually described by the objective function $J$ as

$$\displaystyle J_{\text{min}}(\mathbf{m})=\|\mathbf{\tilde{y}}-\mathbf{y}(\mathbf{m})\|.$$

(2.27)

In case some of the measurements are of less relevance for the model or less trustworthy, the objective function can be modified by including a vector of weighting factors $\mathbf{w}$ that reflects the relevance of the individual measurements $\tilde{y}_{i}$:

$$\displaystyle J_{\text{min}}=\sum_{i=1}^{N}w_{i}\left|\frac{\tilde{y}_{i}-y_{i}(\mathbf{m}).}{\tilde{y}_{i}}\right|$$

(2.28)

It should be highlighted that the back studies must be undertaken immediately after obtaining the recorded measurements in order for the project design and construction procedures to be reviewed and, if necessary, updated without significant delay during the construction/excavation phase [90]. Iterative parameter identification can be automated thanks to the availability of parameter optimization techniques.

A variety of optimization algorithms have been widely utilized to analyse different engineering problems like optimizing geometry, performance optimization, parameter identification, etc. The back analysis techniques are widely used in geotechnical applications primarily for the purpose of calibrating constitutive model parameters for numerical simulation models [48, 65, 70, 93]. Meier et al. [65] provides a detailed review of several optimization algorithms, and their applications in the geotechnical problems.

Despite gradient based methods, evolutionary algorithms are shown to be efficient and reliable in reaching the global optimal solution in a multidimensional space. As a simulation mechanism of Darwinian natural selection, the Genetic Algorithm (GA) starts with a population of solutions and then improves it through repeated applications of selection, crossover, and mutation operators. Khaledi et al. [46] and Müthing et al. [77] used GA to determine the parameters of a time dependent constitutive model.

Particle Swarm Optimization (PSO) is an evolutionary optimization algorithm that was introduced in [44] working with a population (called a swarm) of candidate solutions. This method randomly places a number of ‘‘particles’’ in the search space of a specified function and then evaluates them at each point. Zhao et al. [127] carried out PSO to determine geotechnical parameters for an actual tunneling project (Western Scheldt tunnel). The optimized parameters successfully captured the tunneling-induced ground motions.

2.3.2 Metamodeling

Depending on the size of the subsurface domain, the excavation length, and the appropriate discretization, 3D finite element simulations of the mechanized tunnel can take anywhere from half an hour to several hours to complete. Therefore, the existence of a tool that allows for the execution of a large number of precise and detailed numerical models is required for the use of most of the non-deterministic approaches. This is due to the fact that uncertainty quantification and reliability analyses need thousands of model runs. As a result, using surrogate modeling approaches to replace the tunnel’s original finite element models is essential. Based on a given number of parameter samples conducted in the original finite element (FE) model, several mathematical methodologies have been examined and confirmed. These techniques attempt to determine model input parameters, mainly subsurface mechanical characteristics and boundary conditions, permitting a valid employment of tunneling simulation models.

Surrogate models, also known as metamodels or emulators, are empirically generated models (or mathematical functions) that link the inputs and outputs of a computer model or a complicated system. They originated in the idea of design of experiments (DOE), which employed polynomial functions as a response surface methodology (RSM) [122]. Other metamodels have since been created and used, including kriging [18], artificial neural networks, radial basis functions (RBF) by [51]. RBF later has been extended by [76], and been called extended radial basis functions (ERBF). This method employs more than one basis function for each input which leads to a linear combination of radial- and non-radial basis functions to conduct the approximation. Unlike classic RSM, which simply calculates a least squares distance between data points, these approaches give an interpolation surface that spans all training data points. Furthermore, unlike RSM, which assumes a certain shape for the approximation as polynomials, these approaches often include a series of functions, each associated with individual points in the feature space. [14] presented a surrogate modeling process that combines the proper orthogonal decomposition (POD) method (also known as Karhunen Loe’ve decomposition [41]) with radial basis functions abbreviated as POD-RBF. This technique showed promising results for approximating finite element simulation responses in [10].

After reviewing the state of the art in metamodeling approaches and comparing their characteristics and considering tunneling simulation as an application [45] presented a hybrid technique that integrated POD and ERBF approaches. Khaledi et al. enhanced the POD-RBF method by replacing the radial basis functions with their extended version [76] and abbreviated it as POD-ERBF. Miro et al. [70] suggested a framework for evaluating and selecting the appropriate surrogate model for the approximation purpose.

Among many researches which used metamodeling techniques to replace complex FE models for system identification purposes as [35, 46], Zhao et al. [126] employed metamodels to develop a hybrid estimation concept. In which a small scale submodel is taken out of a larger complex model and continuous simulations are run in this submodel to reduce computing effort. Metamodels are used in three levels to i) correlate soil parameters and nodal displacements on submodel boundaries, ii) correlate soil parameters and tunneling-induced ground movements according to measurements, and iii) correlate tunneling process parameters and tunneling-induced building settlements.

The purpose of a surrogate model is to approximate the response $u$ of a computational model $f(\mathbf{x})=u$ with an approximation $\tilde{u}$. As a result, the model output $u$ may be given as

$$\displaystyle u=\tilde{u}+\epsilon,$$

(2.29)

where $\epsilon$ is the approximation error. The common approach to surrogate modeling is to perform computer runs for $n$ sets of the input parameters $\{\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{n}}\}$, and then using the generated pair points $(\mathbf{x_{i}},u(\mathbf{x_{i}}))$, as training data to construct an approximation to the original model.

Three steps are necessary to do this, namely:

• 1. Selecting an experimental design to generate training data.

• 2. Choosing (or developing) a metamodeling approach and fit its features based on the data presented above.

• 3. Quantifying the approximation utilizing testing data and some error estimates to assess the surrogate model.

Testing data are often created by running the computational model with input parameters different from those used to create the training data. The third step is discussed further below.

2.3.2.1 Accuracy Measures of Surrogate Models

The most significant aspect of a metamodel, as previously stated, is its agreement with the original data, or prediction goodness. One may become aware of the links between model complexity, sample size, and approximation method based on experience obtained from multiple applications of various techniques, but it is difficult to know the metamodel’s estimation accuracy in advance. As a result, every metamodel must be evaluated before being used to guarantee that it is trustworthy.

Mahmoudi et al. [71], applied many measures to identify the extent of perfection in a surrogate model, as Root Mean Square Error (RMSE), normalized Root Mean Square Error (NRMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE), Bias Factor, Nash-Sutcliffe Efficiency (NS), Variance Account Factor (VAF), Performance Index (PI), RMSE To Standard Deviation Ratio (RSR), Normalized Mean Bias Factor (NMBE), Mean Absolute Percentage Error (MAPE), Wilmott’s Index (WI), Legate and McCabe’s Index (LMI), Expanded Uncertainty ($U_{9}5$), t-Statistic, Global Performance Indicator (GPI), and Weighted Mean Absolute Percentage Error (WMAPE).

Additional techniques to investigating the correctness of the metamodel may be found in the literature. The coefficient of prognosis, which is a model-independent statistic to assess model quality, is suggested in [74]. It is used to generate a so-called metamodel of optimum prognosis, which is a rough estimate that excludes irrelevant factors. Atamturktur et al. [4] proposes a coverage metric, in which the coverage of the design space is examined in terms of appropriateness for metamodel development, and where extra samples in the parameter space should be placed to increase the metamodel’s accuracy.

2.3.3 Sensitivity Analysis

In the concept of system analysis, the large number of input factors involved in a sophisticated geotechnical computational model is a challenge. The essential elements that control system reaction and must be calibrated using experimental or field data can be identified using sensitivity analysis.

The approaches used in sensitivity analysis are either statistical or deterministic. Two main categories are the so-called local and the global sensitivity analyses (GSA). To address complicated models including non linear phenomena like a 3D numerical simulation of TBM model advancement, GSA methods are recommended [68]. The performance of different global sensitivity analysis techniques was reviewed in [62]. This study examines three distinct global sensitivity analysis approaches, namely Sobol’/Saltelli, Random Balance Design, and Elementary Effect method. A decision graph is presented to aid in the selection of a proper technique, taking into account several model properties such as complexity, processing costs, and the number of input parameters. Based on the model features, the user may use it as a reference to choose the most appropriate and cost-effective strategy. Sophisticated SA approaches such as Sobol’/Saltelli give additional information as detecting non-linearity and interaction effects for a better understanding of the system. Therefore the designer may be ready to spend for their high computational costs in order to get such knowledge.

One major drawback of global sensitivity analysis methodologies is the requirement to construct a relatively large number of input-output data sets. As a result, the need of advanced numerical models, which are computationally expensive, makes such analysis impractical. The metamodeling notion presented in 2.3.2 is used as a solution.

Among the others, the Sobol’/Saltelli technique, has shown to be particularly useful for a variety of geotechnical systems [127, 69] since it prioritizes parameter relevance and highlights any interactions among them. Its main goal is to determine how the variance of input parameters affects the variance of the model output. The total effect sensitivity index $S_{\mathbf{T}_{i}}$ is a comprehensive index that considers the interaction of variables [91]. In order to employ Sobol’/Saltelli technique, two randomly chosen $K\times 2n$ matrices $\mathbf{C}_{1}$ and $\mathbf{C}_{2}$ are constructed for a generic model with $n$ parameters, where $K$ is the number of samples taken from the model space.

Afterwards, a new matrix $\mathbf{R}_{i}$ is defined by copying all columns from $\mathbf{C}_{2}$ except its $i^{\text{th}}$ column, which is taken from $\mathbf{C}_{1}$. Then, model outputs $f(\cdot)$ for $\mathbf{C}_{1}$ and $\mathbf{C}_{2}$ are evaluated as

$$\displaystyle\mathbf{y}_{\mathbf{C}_{1}}=f(\mathbf{C}_{1}),\quad\mathbf{y}_{\mathbf{C}_{2}}=f(\mathbf{C}_{2})\text{ and }\mathbf{y}_{\mathbf{R}_{i}}=f(\mathbf{R}_{i}).$$

(2.30)

Finally, the variance-based indices for model inputs are evaluated as

$$\displaystyle S_{\mathbf{T}_{i}}=1-\frac{\mathbf{y}_{\mathbf{C}_{2}}\cdot\mathbf{y}_{\mathbf{R}_{i}}-f_{0}^{2}}{\mathbf{y}_{\mathbf{C}_{1}}\cdot\mathbf{y}_{\mathbf{C}_{1}}-f_{0}^{2}},$$

(2.31)

where $\mathbf{y}_{\mathbf{C}_{1}}$, $\mathbf{y}_{\mathbf{C}_{2}}$ and $\mathbf{y}_{\mathbf{R}_{i}}$ are vectors containing model evaluations for matrices $\mathbf{C}_{1}$, $\mathbf{C}_{2}$ and $\mathbf{R}_{i}$, respectively. The mean value $f_{0}$ is further defined as

$$\displaystyle f_{0}=\left(\frac{1}{K}\sum_{j=1}^{K}\mathbf{y}^{(j)}_{\mathbf{C}_{1}}\right)^{2}.$$

(2.32)

Variance-based sensitivity method is not merely used to identify the effectiveness of input factors, but also later employed in Sect.2.3.4 to optimize sensor localisation.

2.3.4 Optimal Experimental Design

The following explanation from [123] can describe the key motivation to pay attention to monitoring design in general: Experiments are expensive and time-consuming to conduct in order to gather a large enough set of experimental data. The goal of optimal experimental design (OED) is to create the necessary dynamic experiments in such a way that the parameters are estimated with the best possible statistical quality from the resulting experimental data, which is usually a measure of the estimated parameters’ accuracy. In other words, the goal is to create the best feasible tests based on model candidates in order to make system identification straightforward. Fisher’s work [27] is widely regarded as the first methodical and scientific investigation of the subject. Fisher implies that the variance of a distribution obtained as an outcome of an experimental design may be used to explain the discovered information content in order to link data to information. As a result, if some components of the monitoring or experimental design are ignored, the resulting distribution will be different and the information content will be reduced. In this way, the designer may compare which experimental design comes closest to a fully monitored scenario while requiring the least amount of experimental work.

To describe the information content $I$ of the experimental data $\tilde{\mathbf{y}}$ with respect to the parameter $m_{i}$, the formulation

$$\displaystyle I=\frac{\partial^{2}\tilde{\mathbf{y}}}{\partial^{2}m_{i}}\;,\;i=1,\dots,s$$

(2.33)

can be employed, where $s$ is the dimension of the considered parameter space. The matrix that accrues when considering all parameters and their correlations is often called the Fisher-information matrix FIM, whereby several similar formulations exist. In [6], the state of the art up to the 1970s is presented and the concepts of [27] are transferred to more systematic and fundamental approaches. This FIM is still employed in recent publications such as [120] that investigated where to place sensors to survey air pollution. In [52], a more statistical investigation is performed on sensor placements on dams, wherein the mean square error of parameter identification results is employed to define the quality of an experimental design. This approach was further developed by the employment of the bootstrap method in [94], where again repeated parameter identification is performed to obtain a covariance matrix $\mathbf{C}_{\mathbf{m}}$ of all considered parameters $\mathbf{m}$. Another aspect in the framework of OED is that one should differentiate between problems where the parameters of interest need to be back-calculated as it is the case in the present thesis and those where they can directly be measured. An example for the latter case is given in [75] where it is described how to find optimal sensor placements to detect contaminants in a water network. As the water demand in such a network is uncertain, finding these optimal placements is still a complex optimization problem, but it does not require the additional step of parameter identification. With different deterministic and stochastic optimization approaches, including different uncertainty scenarios, the optimal sensor locations are identified exhibiting quite different results and showing the need to consider effects of uncertainty in OED applications. The experimental settings can be modified to make the calibration of an unknown (or uncertain) input component as simple as possible. Furthermore, collecting data from tunnel construction measurements enables for the validation of numerical models and the reduction of parameter uncertainties. The utility $\tilde{U}$ (as inverse equivalent to the cost function) defines how a certain design $\boldsymbol{\delta}$ reduces the uncertainty and is to be maximized. Random output samples $y$ are generated according to the defined initial distribution of the input parameter $m$ and the considered ‘‘experimental design,’’ $y=f(m,\boldsymbol{\delta})$.

Hölter et al. [34] used Bootstrap technique to evaluate and compare the specific design scenarios and the aspect of including measurement error in a hydromechanical structure. Among all the various approaches to conduct OED, in this study exclusively employing sensitivity measures for performing OED, and Bayesian updating concept were applied. However, GSA is still performed as first essential step to identify the most relevant model parameters on which the specific OED approach is applied afterwards.

2.3.4.1 Spatial GSA

The benefit of sensitivity analysis in relation to the issue of OED is initially determining which parameters are most relevant. The experimental design should concentrate on these parameters since discovering a parameter that has no impact would be wasteful of the generally limited resources. The conceptual relationship between GSA and OED is that changing the parameters to which the model response is most sensitive results in a wider bandwidth of outcomes. The greater the output variation, the easier it is to identify and distinguish the effect of particular parameters from uncertainty-related errors. As a result, using a back analysis, as explained before in Sect. 2.3.1 back, it is feasible to determine the most sensitive parameters with the greatest accuracy. First ideas to the concept of sensitivity analysis in a spatially distributed manner for geotechnical purposes can be found in [34]. Modern FE programs enable model answers to be provided for any point of the FE model geometry. A GSA may be done for each of these spots to utilize the position with the highest sensitivity to a given parameter to insert a sensor to identify this specific parameter. However, it should be noted that the sensitivity index $S_{T_{i}}$ calculated using the variance-based technique yields normalized values in each spot for all the considered parameters. Therefore, they may not be compared in various locations. This issue can be overcome by including the importance of an output via its variance and using the updated sensitivity index $S_{T_{i}}^{*}$,

$$\displaystyle S_{T_{i,j,k}}^{*}=\frac{S_{i}\leavevmode\nobreak\ \sigma_{j,k}}{\max_{k}\sigma_{j,k}},$$

(2.34)

where, $S_{T_{i,j,k}}^{*}$ denotes the well-known sensitivity index as it was introduced in Sect. 2.3.3 for a certain parameter $m_{i}$, but specifically for the $j^{\text{th}}$ model response obtained at the $k^{\text{th}}$ position. $\sigma_{j,k}$ denotes the standard deviation of the $j^{\text{th}}$ model response obtained at the $k^{\text{th}}$ position and $\max_{k}\sigma_{j,k}$ corresponds to the maximum of the standard deviation of the $j^{\text{th}}$ model response obtained from all of the considered positions. Contour plots may be constructed via interpolation after getting $S_{T_{i,j,k}}^{*}$ in each of the grid points, allowing for improved visualization and explanation of the data. In terms of planning an experimental setup, the contour plot areas with the greatest values of $S_{T_{i,j,k}}^{*}$ are the optimum places to install sensors of the matching response type $j$. The various values of $S_{T_{i,j,k}}^{*}$ should be employed as objective function weighting factors $w_{i}$ in the cost functions defined by Eq. 2.28.

2.3.4.2 Bayesian OED

For several decades, applications of Bayesian updating have been applied in various fields. Miro [68] and Nguyen [78] employed Bayesian interference to update 3D simulation models of tunnel excavations. The uncertainty of the prior estimation of the soil parameters is therein reduced stepwise using measurement data that is obtained after each new excavation step of the tunnel, but each time affected with artificial random noise. As the measurement data used for back calculation is at the same time an extension of the current data knowledge, one might be interested to ‘‘update’’ the previous knowledge. This concept was first formulated in [7] as

$$\displaystyle p(m|y)=\frac{p(y|m)\leavevmode\nobreak\ p(m)}{p(y)}.$$

(2.35)

Herein, $p(y)$ describes the probability distribution function (PDF) of model output that is used to normalise the result. Here, this would typically be noisy measurement data $\mathbf{\tilde{y}}$ that is somehow distributed around its mean value $\bar{y}$. $p(m)$ accordingly is the PDF of the model parameters. These would usually be soil parameters that are often very uncertain in geotechnical engineering. Within the Bayesian concept, this distribution $p(m)$ is called as ‘‘prior knowledge.’’ Accordingly, $p(m|y)$ is called the posterior knowledge as it includes the new information $y$. The link between prior and posterior distribution is the likelihood $p(y|m)$ that describes how probable the new data $y$ is, given the known probability distribution of $m$.

2.3.5 Case Study: The Metro Line 5 in Milan

The Metro Line No. 5 in Milan is selected as an exemplary realistic case study to show the use of previously mentioned approaches. This route, which runs from the north to the west of the city, is composed of 2 12.6-kilometer tunnels with a center-to-center distance of 16.7 meters between them. The first tunnel was completed in May 2012, and the second tunnel was completed a month later in June. The outside diameter of the tunnel tubes is $D=6.7$ m. Tunnel excavation was carried out utilizing EPB machines (tunnel boring machine with earth pressure balance shield). In the segment under consideration, the tunnel axis is 15 meters below ground level. [24] developed an FE investigation to analyse the soil-structure interaction behavior that is induced by the construction of the twin-tunnel. This simulation of three soil layers using the HSsmall model [8], was used in our study as well. The subsoil consists of a 20-meter-deep gravelly sand layer, lies beneath a 5-meter-thick sandy silt soil layer, according to the geotechnical soil research. Finally, a gravelly sand with a thickness of 5 m (i.e. 25–30 m below ground level) was discovered. For the finite element simulation, drained conditions are considered because of the high permeability of the soil (gravelly sand). This model was created with the FE-code Plaxis 3D and is presented in Fig. 2.24 without the soil clusters. Table 2.2 lists the soil parameters derived from the soil study and subsequent laboratory testing, as reported by [23, 24]. The considered twin tunnel is excavated in an urban area and partially underpasses a nine-story building. The building that is specifically considered in this model is selected because an extensive monitoring program has been applied to it. Figure 2.25 depicts the building’s location and relationship to the two tunnel tubes. The shallow foundation of the residential structure comprises five strip footings and intermediate concrete slabs. With a height of 0.65 m, the strip footings are placed around 4 m below ground level. Figure 2.25 also shows the monitoring arrangement, comprising 13 sensors placed throughout the building. The sensors capture local vertical displacements. At the same time, the location of the TBM, applied face pressure, and grouting pressure are recorded. This allows the numerical model to be validated, as well as, to some extent, the outcomes of an OED procedure.

Fig. 2.24

FE model of considered interaction of twin tunnel bypassing the nine-storey building, [103]

Tab. 2.2 In-situ soil parameters according to [24]

Fig. 2.25

Top view of the considered building and location of applied measurement points [103]

The ultimate goal of design, monitoring, and back calculation is to prevent compromising the integrity and serviceability of subsurface and above-ground structures. If an appropriate model that can very accurately anticipate building behavior is produced, countermeasures that lead to improved building safety may be more effectively assessed. As a result, the goal becomes to produce a trustworthy model by identifying the important soil features using the approach of back analysis outlined in Sect. 2.3.1, which will benefit from incorporating OED principles.

In the previous studies by the authors, e.g., in [103] the in-situ measurement data were employed to back-calculate the constitutive parameters of the surrounding soil. In that study, the grouting pressure $p_{\text{v}}$ and face pressure $p_{\text{s}}$, the site-related volume loss factor $V_{\text{L}}$, the friction angle $\varphi_{1}$, the small-strain stiffness $G_{0,1}$, and the secant stiffness $E_{50,1}^{\text{ref}}$ of the first and the second soil layer, $E_{50,2}^{\text{ref}}$ were evaluated to be the most important parameters. It should be noted that the secant stiffness $E_{50}^{\text{ref}}$ is supposed to be associated with the tangent stiffness $E_{{\text{oed}}}^{\text{ref}}$ and the unloading-reloading stiffness $E_{{\text{ur}}}^{\text{ref}}$, by a factor of three. When the term ‘‘stiffness’’ is used in the following, it refers to those three factors. Only the measurement data received until the first tunnel tube is completed is used for model validation, so that a forecast for the excavation of the second tunnel tube may be made and compared to the measurement data. As a consequence, the findings shown in Fig. 2.26a, are achieved. The measured settlements obtained after excavation of the first tube in the thirteen measurement points shown in Fig. 2.25 are displayed here, along with the settlements that correspond to the identified parameters using the actual FE-model and the corresponding metamodel. The determined set of parameters is utilized for subsequent experiments and for the prediction of the settlements produced by the excavation of the second tube, as illustrated in Fig. 2.26b. The findings of the FE-model are compared to the data when the second tube is completed. With the exception of R4, T1, T2, and T3 points, there is still a strong agreement. One should keep in mind that, in the considered urban region, there are other buildings just adjacent to the one being studied, that produce pre-stressing of the subsoil and consequently an increase in stiffness, resulting in the lower settlements observed in reality.

Fig. 2.26

Comparison of measured and a back-calculated data of first tunnel excavation and b measured and predicted data of second tunnel excavation [33]

Several GSAs are done in [103] to gain a better knowledge of the system behavior, linking the aforementioned soil and system characteristics to average settlements and tilting along different axes of the building. The results of the GSAs performed following excavation of the first and second tunnel tubes are presented in Figs. 2.27 and 2.28, linking the seven examined input parameters to the vertical settlements of each of the thirteen measurement locations. When looking at the shown findings, it is clear that they change with time and space, but that the parameters $E_{50,1}^{\text{ref}}$, $G_{0,1}$, and $V_{\text{L}}$ have the most impact on the analyzed outcomes. As a result, all subsequent research, have focused only on these three parameters.

Fig. 2.27

GSA results utilized in thirteen measurement places to examine the influence of the seven factors of interest on settlements after the first tunnel tube was excavated [33]

Fig. 2.28

Results of GSA applied in the thirteen measurement points considering the impact of the seven parameters of interest on the settlements after excavation of the second tunnel tube [33]

In a further step, a second GSA was run for the previously discovered key parameters to examine the evolution of the sensitivity of the model response in time and space domains with respect to each of the key parameters defined from GSA. The main idea of spatial GSA as a tool for OED concept is introduced in [37]. This GSA is used in the same way as previously to find geometrical sections that are particularly promising for sensor positions, but with the output values of different places in the relevant area. Schoen et al. [102] analysed the spatial and temporal variations in the sensitivity of different parameters in various construction stages, namely during the passage of first tunnel, at the end of excavation of the first tube, and finally when both tunnels are bored. They concluded that the influence of the secant stiffness $E_{r}^{\text{ref}}$ on the settlements increases with progress of the tunnel excavation. Moreover, $V_{L}$ has a high influence on the settlements around the TBM as surface settlements are directly related to the volume loss. Zhao et al. [125] also showed that the sensitivity of the volume loss $V_{L}$ depends on both the location of the TBM, and the magnitude of the surface loads above the tunnel. The spatial GSA findings reveal that the impact of each input parameter changes geographically and temporally depending on the excavation time step and location. As a result, the usefulness of monitored data for parameter identification changes depending on the position of the sensor and the period of monitoring. Therefore, in parameter identification process, it is far more necessary to utilize data from those sensor locations that are particularly impacted by the respective input parameter at the most. Afterwards, the GSA findings are utilized as weighting factors for each monitoring spot and each input parameter in the cost function for back analysis. These weighting variables are chosen based on spatial GSA results to provide more weight to those measuring places where the effect of the corresponding input parameter is considerable, and significant tunneling-induced settlement can be accurately recorded. Therefore, their values vary in different construction phases. Including these weighing factors in the back analysis improves the simulation model’s accuracy, bringing it closer to the in-situ records.

Continuation of this research in relation to monitoring optimization, Hölter et al. [36] employed the introduced Bayesian OED using the Approximate Coordinate Exchange (ACE) in Sect. 2.3.4 to use obtained prior knowledge for improving the further searches. After excavating the first tunnel tube, the vertical settlements are acquired at a grid of locations separated by 5 m within the constraints of the employed FE-model. Latin hypercube sampling technique is used to build a sample set of 120 combinations of the three parameters of interest, to generate a metamodel for the FE-model. The metamodel is generated based on quadratic polynomial regression, allowing the settlement result to be received in any of the 259 parameter combinations. To calculate settlement data between these points, the polynomial interpolation approach described in [2] is used.

It is specified that six sensors should be located in this region. Because each sensor location may be swapped in both dimensions of the surface, determining the ideal design $\boldsymbol{\delta}$ becomes a twelve-dimensional optimization issue. To begin, a random 6 $\times$ 2 matrix inside the provided geometric limits should be simply constructed. It should be noted that the initial design $\boldsymbol{\delta}_{0}$, which determines where the ACE algorithm begins its search, has a significant impact on the method’s performance. For example, if certain places of the model’s boundaries which are not affected by the building or tunnel excavation at all are chosen, the calculations result in high utilities and the model reaction will always be the same. Accordingly, none of the investigated current designs is accepted as new best design $\boldsymbol{\delta}^{\dagger}$ and the initial design $\boldsymbol{\delta}_{0}$ is always kept. As a result, it is reasonable to position the starting coordinates of the six sensors anywhere within the tunnel’s area of impact, such that the different back analysis runs result in varying responses of the utility function $u$.

The obtained results are shown in Fig. 2.29. The settlement at the ground surface in the whole model domain is illustrated as a contour plot between red and green for one typical parameter combination, with the position of the building noted as a black block. The locations of the sensors in the first design $\boldsymbol{\delta}_{0}$ are represented by white squares. They are clearly located in locations where big settlements occur for the reasons stated above. The black crossmarks represent the ultimate design to which the algorithm converges, i.e. the design with the highest utility. The black markings may be seen moving away from the initial design and towards the border of the settlement basin. It should be noted here that the settlement distribution refers to a single arbitrary realization of the input parameters $\mathbf{m}$. The settlement distribution may be broader or smaller for various combinations. The resulting sensor configuration does not correlate to a specific set of parameters, but it is expected to be the most reliable throughout the studied range of values.

Fig. 2.29

Initial design $\boldsymbol{\delta}_{0}$ and final design $\boldsymbol{\delta}^{*}$ of the Bayesian OED mapped over displacement field of the ground surface. The position of the building is shown in black [59]

2.3.5.1 Reliability Measures Updating

As mentioned before, engineers use inverse analysis techniques to increase the dependability of proposed infrastructure projects such as mechanized tunnels by evaluating the uncertainty propagation of soil parameters using recorded data. During different excavation phases, the excavation-induced settlement of the surface structures impacted by tunneling projects is commonly monitored. However, the strength characteristics of geomaterials, on the other hand, shows spatial variability owing to their natural origin. Model adaptation, which is primarily concerned with using previously acquired dataset in further prediction, may be used to precisely analyze the impact of uncertainties on dependability measurements. In this study, a recently developed approach for Bayesian updating of reliability is used while applying random field techniques to account for the geographical variability of the subsoil. The revised reliability measures may be calculated. They can be used to identify the right steering settings or to select adequate countermeasures in order to minimize long-term damage.

In this procedure, the spatial random variables are adjusted depending on the measured data from the mid-term excavation phase. After that, the updated dependability metrics for subsequent phases are being estimated. The introduced method is applied on the finite element simulation of the twin tunnel project introduced in 2.3.5. The collected findings demonstrate how the reliability update concept may be used to determine the long-term viability of an initial geotechnical design for a mechanized tunneling project.

2.3.5.2 Random Field

In general, mechanized tunneling is often regarded of as a massive geotechnical project over a broad region. Almost all attributes of subsoil must be handled as heterogeneous materials owing to variation in lithological composition, stress history and sedimentation, weathering and erosion, probable faults and fractures. As a result, for every stochastic analysis, peculiarities of the spatial distribution of geological and geotechnical should be characterized and taken into consideration.

Regression analysis, geostatistics, and random field theory are three basic kinds of statistical approaches for estimating spatial variability that have been established. Regression techniques presume that all sample values within a medium have an equal and independent probability, i.e., that they are not autocorrelated, which contradicts field observations show that samples obtained closer together have a larger association than ones taken further apart. As a result, regression approaches are better suitable for preliminary analysis when just a small number of samples with wide distances between them are collected from the site [87]. However, the autocorrelation approach in geomaterials is taken into account in the other two categories.

Here, the Karhunen-Loève expansion method, which is extensively utilized in random field theory, is applied [109, 29]. The spectral decomposition of the covariance function is used in the Karhunen-Loève expansion, which may be written as

$$\displaystyle\hat{H}(x,\theta)=\mu_{H}(x)+\sigma_{H}(x)\sum_{i=1}^{M}\sqrt{\lambda_{i}\leavevmode\nobreak\ \Phi_{i}(x)\leavevmode\nobreak\ \xi_{i}(m)}.$$

(2.36)

The eigenvalues and eigenfunctions of a Fredholm integral equation, where the auto-covariance function (i.e., autocorrelation function multiplied by the variance of the random field) is specified as a kernel, are $\lambda_{i}$ and $\Phi_{i}(x)$, respectively. The mean and standard deviation are represented by $\mu_{H}(x)$ and $\sigma_{H}(x)$, respectively. $M$ is the number of series terms in the equation, and $\xi_{i}(\theta)$ is a vector of uncorrelated random variables that represents the unknown parameters’ randomness. This vector will be subjected to modifications in a Bayesian way later on in the model adaptation context. The further details regarding random discretisation can be found in [61, 63]. A random field discretisation example of Elastic modulus is shown in Fig. 2.30.

Fig. 2.30

Random field exemplar

2.3.5.3 Bayesian Back Analysis

With a given performance function $G_{x}$, the failure event is defined as

$$\displaystyle P_{F}=P[G_{x}\leq 0]=\int f_{(x)}\text{dx},$$

(2.37)

where $f_{(x)}$ is the joint probability density function of $x$, $x$ being the vector of uncertain input variables.

Straub [106] presented the Bayesian back analysis approach, which is used here.

Employing the aforementioned Milan Metro tunnel in Sect. 2.3.5, Mahmoudi et al. [59], performed a reliability analysis at the end of the second tunnel excavation, merely considering the spatial uncertainty of material parameters. Afterwards, the Bayesian reliability updating concept is utilized to take into account the settlement recording at the end of first tube excavation. The ground measurement is assumed to be recorded equal to 12, 9 and 2 mm at the measurement point from left to right after the excavation of the first one is completed. These values are less than average amounts observed for the homogeneous cases. Figure 2.30 depicted a typical random field discretization generated by Karhunen-Loe’ve expansion. The spatial arrangement of random field will be changed after applying the Bayesian updating technique. The results show a particular change in the reliability measures prediction through considering the mid-term measurements. In addition, the effect of the arrangement and accuracy of the sensors on the reliability measures were investigated. Table 2.3 shows the change in the failure probability indices before and after Bayesian updating. Here the Mid-term measurement represent the monitored ground settlement at the middle of two tunnels. The considered error for the measurement is noted by $\sigma_{m}$, the updated reliability index and correlated probability of failure were shown by $\beta$ and $P_{f}$, respectively. The reader is referred to [59] for detailed information about the applied techniques to obtain the reliability measures and updating them.

Tab. 2.3 Reliability measures updated by mid-term measurement

2.3.6 Pattern Recognition

Geotechnical construction has historically employed sensing technology for a variety of objectives, including identifying geological irregularities, health structure monitoring, and ensuring integrity. Using common instruments in geotechnics as e.g., strain gauges, load cells or piezometers, a vast amount of data in the form of time series will be provided, specifically, in large projects like tunneling. The high dimensionality and feature correlation of large time series databases, along with noises, is an evident challenge when studying them. This challenge can be overcome by using automated pattern recognition algorithms to time series for translating a dataset representation of an item or relationship to an output category. The data logs of pore water pressure and ground settlements recorded by a TBM during tunnel excavation are assessed in this work. Due to the different stress distribution in the soil domain as a result of different geological formation, the resultant vertical displacements and water pressure logs may vary substantially during tunneling. As a result, the changes in sensor data trend or motif may be identified and labeled across different geological conditions through supervised learning methods. Pattern recognition is referred to as a supervised learning process when a given pattern is assigned to one of the pre-defined classes using pre-labeled data to construct a model. A supervised machine learning (SML) algorithm can identify correlations and patterns in the fluctuation of observed data and correlate it to potential geological formation changes.

The Support Vector Method (SVM) [17], is used in this work as a well-known approach for conducting SML. Several scholars have used SVM in geotechnical engineering problems, tunnel excavation design, and reliability analysis [38]. Yao et al., [124] used SVM to forecast the displacement of the surrounding rock of a railway tunnel for tunnel safety estimation. Mahdevari et al. [58] used this technique as a nonlinear regression approach to forecast tunnel convergence after excavation. The results of performing SVM and K-Nearest Neighbor (KNN) analysis were presented by the authors in [60]. The learning process in human brains is the motivation for neural nets. A neural network is made up of a linked graph of perceptrons, each of which receives input from previous levels and passes output to subsequent ones. The weight supplied to each individual link, which is determined by the cost function and the optimizer, determines how each layer output becomes the input for the following layer. The ultimate findings of a classification task are really probabilities. The input dataset will be assigned with the label that received the highest probability. A neural network, on the other hand, has a lot of hyperparameters to adjust. To successfully comprehend diverse datasets, multiple sets of hyperparameters are required. However, the enormous number of hyperparameters makes it difficult to identify their values to achieve an accurate prediction/classification results. Therefore, finding the appropriate settings of hyperparameters to create the model from a certain dataset requires hyperparameter tuning. For instance, the number of neurons, activation function, optimizer, learning rate, batch size, and epochs are the hyperparameters to be modified. Although, there are several techniques concentrating on optimizing the hyperparameter evaluation, the problem of determining the right combination of hyperparameters remains a challenge. In this study, a network for optimization using the stochastic gradient descent learning technique established in [89] is used. It includes five hyperparameters, namely, the number of neurons in hidden layers, epochs, learning rate, batch size, and lambda value. In order to tune these parameters a grid search is conducted.

In the following, the neural network concept as another supervised learning method, is applied to predict any geological distortion ahead of a TBM excavating a 8.5 m tunnel in the depth of 8.5 m. In order to train and validate the network, the gathered data from 10 ground settlement and ten pore water pressure sensors are employed. The details regarding the system configuration is explained by the authors in [88].

In order to measure the accuracy level of trained neural network, various indications can be used, namely accuracy, recall, precision and F1-score. They can be obtained as

$$\begin{aligned}\text{Accuracy} & =\frac{T_{P}}{T_{S}},\end{aligned}$$

(2.38)

$$\begin{aligned}\text{Precision} & =\frac{T_{P}}{T_{P}+F_{P}},\end{aligned}$$

(2.39)

$$\begin{aligned}\text{Recall} & =\frac{T_{P}}{T_{P}+F_{N}},\end{aligned}$$

(2.40)

$$\begin{aligned}\text{F1-score} & =2\frac{1}{\frac{1}{\text{Precision}}+\frac{1}{\text{Recall}}},\end{aligned}$$

(2.41)

where $T_{P}$ indicates the number of cases in which machine predicted the right class, and $T_{S}$ is the number of all the validation test data. $F_{P}$ and $F_{N}$ denotes the false positive and false negative cases. Regarding multi-class cases as the present study, the precision and recall values are firstly calculated for all the classes, and finally use the mean value as a general metric.

The calculated metrics in various distance between the TBM face and the geological anomaly is represented in Table 2.4. In this neural network, 5% white error is assumed for the pore water and settlement gauges. The obtained results show acceptable accuracy level for all the cases, however, the prediction accuracy increased when the distance decreased.

Tab. 2.4 In-situ soil parameters according to [24]

The highest accuracy in classification, according to the data in [59], belongs to the combination of kriging and KNN, which improves recognition accuracy even when the excavation is taking place at a distance from the anomaly. However, the SVM and neural network accuracy is sufficient for scenarios when the anomaly is predicted in the near field, despite the fact that it requires less computing work.

2.4 Three-Stage Concept

The previously explained methods of the current chapter can be combined into one hybrid method to improve the prediction of the subsoil properties as well as to reduce computational demand. In [88], a three-stage concept is presented which combines the pattern recognition approach (Sect. 2.3.6), UHSA (Sect. 2.2.3.1), and the adjoint approaches in time (Sect. 2.2.4) and frequency (Sect. 2.2.6) domain. The concept is shortly explained in the following, where an overview of the three-stage exploration approach is given in Fig. 2.31.

Fig. 2.31

Overview of the three-stage exploration approach. (Reproduced with permission from Elsevier from C. Riedel et al. ‘‘A hybrid exploration approach for the prediction of geological changes ahead of mechanized tunnel excavation’’. In: Journal of Applied Geophysics, 203, p. 104684 (2022))

In the first stage, pore water pressures and ground settlements are continuously recorded while the tunnel is excavated. The acquired data is processed by the pattern recognition approach in order to identify a potential anomaly. To do so, various machine learning algorithms are trained for different scenarios, e.g. a fully homogeneous model, an interlayer, a layer change or a boulder. The applied supervised methods, namely SVM and KNN shown high accuracy to classify the geological condition ahead of TBM, merely based on the monitored settlement and pore water pressure variation. If the SML approach successfully identifies an anomaly, the TBM is stopped in order to perform a seismic survey. Subsequently, the second stage is initiated, which is FWI with UHSA. Here, all available knowledge derived from the SML approach is processed, where the predicted scenario of the SML approach is used to implement a parametrization of the anomaly. UHSA might already bring a sufficient prediction; however, it is probable that some parts of the anomaly are not reconstructed in its entirety because the chosen parametrization might not be able to describe all features. Therefore, the third stage is executed in the form of adjoint FWI, where the final model of UHSA is used as the initial model. Both the time domain and the frequency domain approach can be used in order to finalize the prediction of the subsoil properties and to image further details. In [88], the three-stage concept is successfully tested with synthetic data, where the reference model contains a boulder. Each of the three stages can improve the image of the anomaly and on the basis of the final prediction, the location, shape and material properties of the boulder can be precisely estimated.

2.5 Soil-Shield Machine – Interactions

This chapter summarizes some result from a research focused on identification of ground conditions by analyzing machine data during excavation of shield driven tunnels in soils. The goal of this research is to utilize TBM machine data for estimating soil properties. Particularly data about movement of the cutting wheel and the shield with respect to subsoil conditions have been analyzed. Towards this goal, the geological and geotechnical properties of subsoil have been continuously evaluated and the raw machine data collected at a hydro-shield project. The raw data have been separated between active and passive parameters: Active parameters are set by the operator and include the cutting wheel rpm and pressure of thrust cylinders. Passive parameters (thrust force on cutting wheel, torque on cutting wheel, advance speed and rate of penetration) are the result of active parameters. The latter are termed excavation-specific data components which may serve as an indicator for the influence from the ground’s resistance to excavation (ground conditions) and for the influence of the state of the cutting wheel (design of the wheel, state of tool wear and clogging), respectively.

2.5.1 Excavation-Specific Data Components

Table 2.5 distinguishes between excavation-specific and excavation-independent raw TBM data. Those data must be revised for arriving at meaningful interpretations of interactions between a TBM and the ground [22, 32]. For example, the total thrust force $F_{\text{Th}}$ of the shield machine (raw data) must be stripped from excavation-independent data as shown in Fig. 2.50 to arrive at data of tool forces $F_{\text{T}}$ to be compared with the soil condition. The detailed procedure is given in [22].

Tab. 2.5 Excavation-specific and excavation-independent components of machine raw-data

To connect machine data with soil conditions the following should be considered. The penetration rate $\text{Pen}_{\text{raw}}$ is a target value in shield tunneling and requires a certain contact force $F_{\text{con}}$ of the cutting wheel for soil with a given resistance to be excavated. Additionally, the torque at cutting wheel $M_{\text{raw}}$ is a function of the specified penetration rate $\text{Pen}_{\text{raw}}$ and the resistance of the soil to be excavated. It is defined accordingly

• specific torque $M_{\text{spec}}=M_{\text{raw}}/\text{Pen}_{\text{raw}}$,

• specific penetration $\text{Pen}_{\text{spec}}=\text{Pen}_{\text{raw}}/F_{\text{con}}$.

There are some general connections of the resistance of the soil with the specific torque moment and the specific penetration as shown in Table 2.6.

Tab. 2.6 Tendency of excavation resistance for the main soil types (SPT-values [112, 67])

Fig. 2.32

Schematic presentation of forces acting on cutting wheel of a hydro-shield machine: $F_{T}$: tool forces; $F_{S}$: resulting force of face support pressure acting on area of cutting wheel drive; $F_{B}$: internal friction forces of main bearing; $F_{C}$: internal friction force of hydraulic cylinders; $F_{\text{Th}}$: thrust force on cutting wheel raw-data [21]

2.5.2 Case Study: Application to a Hydro Shield Project

A reference project, involved a 2.27 km long tunneling project of diameter 9.5 m driven through terraced rubble of the quaternary near the river Rhine is considered. Details about the project, the TBM and the geology and can be found in [21]. The soil consists of sand and gravel as shown in Fig. 2.33.

Fig. 2.33

Typical soil (left) and screenlines (right) at the hydro-shield drive [21]

The raw TBM data were processed as described above and plotted in Fig. 2.34. The wide spread of the specific penetration can be attributed to different geological conditions at the face as shown in Fig. 2.35.

Fig. 2.34

Plot of specific torque vs. specific penetration at the hydro-shield project [21]

Fig. 2.35

Correlation of data with site conditions [21]

To compare different projects with different shield machines the specific contact force (SCF), which is contact force $F_{\text{con}}$ divided by the area of the cutting wheel $A_{\text{CW}}$, is computed. The Force Index FI is introduced as

$$\displaystyle\text{FI}=\text{Pen}_{\text{raw}}/\text{SCF},$$

(2.42)

and the Torque Index TI,

$$\displaystyle\text{TI}=M_{\text{spec}}/A_{\text{CW}},$$

(2.43)

and show the plots in Fig. 2.35.

Fig. 2.36

Force-Index vs. Torque-Index plots for a wide range of case studies [21]

The different lines of the TI-FI plots reflect the different designs of the cutting wheel and TBM specifics. Analysis of the soil conditions at the various projects leads to Fig. 2.36. The torque of a shield TBM is mainly attributed to the shear strength of the soil and contact force is attributed to the packing density or consistency of soil.

Fig. 2.37

Dependency of the torque index to the force index with respect to the shear strength and packing density [21]

For future studies it is possible to employ soil characteristics from site investigation to estimate the magnitudes of FI and TI, respectively. For a given penetration rate (the target parameter) the torque and the contact force of the cutting wheel may be tentatively estimated.

2.6 Monitoring of Building Damages by Radar Interferometry

One important aspect of the settlement damage research was the monitoring of building damages using both traditional terrestrial- and advanced satellite-based monitoring techniques. Also, a combination of terrestrial and extra-terrestrial proved to be of valuable service to TBM operators. Of course, this presupposes proper damage assessment methods with validated mathematical and engineering theories are readily available.

2.6.1 On the Importance of Settlement Monitoring for the Management of Damage for Inner-City Tunnel Construction

The continuous increase in traffic volumes in metropolitan areas gives rise to further construction of underground transport facilities. Typical examples are road or subway tunnels usually driven by mechanized shield tunneling. This trend densifies the traffic facilities in the underground and consequently reduces the coverage of existent building structures [82].

With inner-urban tunneling projects reports on actual or potential damages due to settlements of existing structures often predominate in the press. Such reports unmistakably reflect the concerns of citizens and residents and let problems of acceptance arise that must be expected to extend the construction period already in advance. Thus, in particular the risk of damage to existent structures above-ground comes to the attention of developers and construction companies at an early stage [66].

A look into the past shows that this topic was already taken up in the 1950s when some rudimentary recommendations for the prediction of structural damage were first developed. However, significant influences from the settlement event itself, as well as the building materials and key properties of the structures, were not taken into account. It was not until the 1970s that Burland & Wroth [16] published their approach that is still current today, which made a semi-empirical prediction of potential damages to buildings due to tunneling-induced settlements possible.

Up to now published semi-empirical approaches to compute vertical settlements can be differentiated with reference to Fig. 2.38 into

• transversal 2D-approaches: Peck (1969), O’Reilly & New (1982), New & O’Reilly (1991), and Mair (1996);

• longitudinal 2D-approaches: Attewell & Woodman (1982) and

• 3D-approaches: Attewell (1982).

Fig. 2.38

Spatial extent of the settlement trough due to tunneling [95]

In addition to its stiffness, the effective displacement of the structure is of central importance in the evaluation of structural damage caused by tunneling-induced settlements. Due to (too) far-reaching simplifications, e.g. with regard to the often highly heterogeneous building stock, the approach according to Burland & Wroth shows deficits that may lead to conservative but also to uncertain evaluation results. In tunneling practice, in particular (too) conservative evaluation results, intended to protect the structures, lead to expensive and time-consuming auxiliary measures (e.g. compensation injections).

2.6.2 Recent Methods of Damage Assessment Due to Tunneling Induced Settlements

Skempton & MacDonald [105] developed the first purely empirical approach to evaluate damages to above-ground structures due to settlements. The evaluation criterion for damages therein are the so-called angular distortions $\rho/L$ or $\beta$, i.e., purely shear-based structural deformations. Limiting values of these distortions classify the extent of damage according to Table 2.7.

Tab. 2.7 Limits of angular distortions $\rho/L$ or $\beta$ according to [105]

Fig. 2.39

Definition of structural rotation and translation: deflection ratio $\Updelta/L$, tilt $\omega$, rotation $\theta$, angular strain $\alpha$ and angular distortion $\beta$ [95]

Burland & Wroth (1974) [16] and Burland et al. (1977) [15] recognized the deficits of a purely shear-based approach and published an enhanced semi-empirical approach to damage assessment, the Limiting Tensile Strain Method (LTSM). The basis of their approach is the transformation of the structure into an equivalent mass-less beam with a shear extension according to Timoshenko (1955) [113]. They recommend the evaluation of damage by means of the limiting tensile strain $\varepsilon_{\text{lim}}$, which indicates the onset of cracking and is defined as the ratio of the relative deflection $\Updelta$ of the beam to its length $L$, the so called deflection ratio (cf. Fig. 2.39). Assuming the neutral axis at the center of gravity of the beam, they derived the analytical equations Eqs. 2.44 and 2.45. Thereby $\varepsilon_{b,\text{max}}$ is the maximum bending strain due to direct tensile loading and $\varepsilon_{d,\text{max}}$ is the maximum shear strain caused by diagonal tensile loading (cf. Fig. 2.40, middle).

$$\begin{aligned}\dfrac{\Updelta}{L} & =\left(0.167\dfrac{L}{H}+0.25\dfrac{H}{L}\dfrac{E}{G}\right)\varepsilon_{b,\text{max}},\end{aligned}$$

(2.44)

$$\begin{aligned}\dfrac{\Updelta}{L} & =\left(0.65\dfrac{L^{2}}{H^{2}}\dfrac{G}{E}+1\right)\varepsilon_{d,\text{max}}.\end{aligned}$$

(2.45)

In Eq. 2.44 and Eq. 2.45, the stiffness of the structure is estimated by the moment of inertia of the equivalent substitute beam with length $B$, height $H$, shear modulus $G$, and Young’s modulus $E$. The dimensions of the structure and the substitute beam are identical. Roof superstructures are not considered in the determination of $H$ (Fig. 2.39). The influence of the estimated bending stiffness $EI$ on the shape of the settlement trough is neglected in their approach, which makes the evaluation of the structural damage again conservative. The green-field settlement trough itself – as the damage-inducing event – can be determined using the approaches from Sec. 2.6.1 [97].

Fig. 2.40

Damage assessment scheme acc. to Burland and Boscardin [95]

The damage categorization proposed by Boscardin & Cording [11] finally relates Burland’s limiting tensile strain $\varepsilon_{\text{lim}}$ to the expected damage at a structure. Moreover, damaging contributions of horizontal strains could be integrated to the LTSM approach which practically comprises four steps (cf. Fig. 2.40):

• 1. predict the green-field settlement trough,

• 2. define the substitute beam and apply settlements in green-field conditions,

• 3. compute bending and shear strains and

• 4. match the relevant strains to a damage category.

To limit the settlement trough’s region of influence, Mair et al. [64] proposed the 1 mm settlement line. For long structures that span several regions of the green-field settlement trough, only those parts within that boundary are to be considered.

2.6.3 Overview and Options for the Monitoring of Settlements

As mentioned above, the two most important approaches to settlement monitoring include traditional terrestrial monitoring and advanced satellite-based monitoring. A strategic combination of terrestrial and extra-terrestrial monitoring proved to be even more advantageous when the synergetic aspects of these methods were exploited.

2.6.3.1 Terrestrial Monitoring

Above all, the risk of damage can be more accurately assessed, controlled, and also predicted by monitoring or surveillance of above-ground structures. State of the art are terrestrial methods that record mainly vertical displacements of structures due to shield driving at the foundation or at the street level (e.g., barometric by tube water leveling). However, three-dimensional monitoring, i.e. the measurement of displacements in all coordinate axes including rotations, among others, with fully automatic total stations (Fig. 2.41), has already been proven suited several times. A recent example is the new metro crossing Amsterdam from north to south, where fully automatic measurement systems were used to monitor the facades of settlement-sensitive historic buildings. Regardless the devices used, all methods must

• 1. provide a sufficient short measuring cycle,

• 2. record data reliable over longer time periods and

• 3. should be highly accurate.

Fig. 2.41

Left: reflector applicable on tripods or an a facade, right: Measurement with tachymeter (total station) acc. to [95]

The accuracy of terrestrial methods is usually $\pm$0.2 mm per 100 m for total stations; leveling (e.g., barometric by tube water leveling) achieves less than 0.2 mm (per 100 m) or up to 0.1 mm. Terrestrial settlement monitoring does not consist of individual measurements, but of the interaction of all (settlement) measurements before, during and after a tunnel construction measure. The boundary conditions and the scope of measurements, including the methods used, are defined in a so-called measurement program. This takes into account the expected settlement sensitivity (vulnerability) of individual structures [66, 82].

2.6.3.2 Satellite-Based Monitoring by Radar Interferometry (Synthetic Aperture Radar, SAR)

Since the launch of the German radar satellite TerraSAR-X, remote sensing systems for settlement monitoring in large urban areas have become competitive due to the increased geometric resolution of the radar system [5]. On-site installations, e.g. in buildings, are no longer required. The method records complex raw data signals (amplitude and phase information) of radar waves (electromagnetic waves) reflected at the Earth surface (Fig. 2.42). Suitable natural radar reflectors are metallic objects or parts of buildings, e.g. a window sill. These are visible as bright spots in the radar image (SAR image, Fig. 2.43). Water surfaces and vegetation in forests or open spaces reflect the radar waves poorly or even not at all and thus stay dark in radar images. Therefore, radar-interferometric settlement monitoring is particularly suited in urban areas. For open spaces, additional measures as installation of artificial reflectors becomes necessary.

Fig. 2.42

Principle of radar interferometry (simplified) according to [19]

Fig. 2.43

Radar scan by SAR with reflections of different strength [19]

The signals recorded by the radar sensor must be spatially and temporally stable to allow for superposition (interference) of two wave signals (coherent radar signals). By comparing two phase positions $\phi_{i}$ recorded from slightly different satellite positions (SAR1 and SAR2) at the same position of an object, the interferometric phase $\phi$,

$$\begin{aligned}\phi=\phi_{\text{flat\_Earth}}+\phi_{\text{topo}}+\phi_{\text{disp}}+\phi_{\text{path}}+\phi_{\text{noise}}+n2\pi,\end{aligned}$$

(2.46)

can be calculated (phase shift). If the other components of the interferometric phase remain sufficiently stable, the phase fraction $\phi_{\text{disp}}$ can be used to infer the displacement, e.g. of a natural radar reflector like a window sill. The displacement is then to be converted from the satellite’s ‘‘line of sight’’ into the sought components of the vertical settlement or uplift. With the SAR method for acquisition and evaluation, the physically limited resolution in azimuth direction is increased by combining multiple images from different satellite positions.

However, in general, the interferometric phase $\phi$ is composed of several components that can have a significant impact on the accuracy of the method. Beside the target deformation $\phi_{\text{disp}}$ the further components are assigned to the impact of the Earth curvature $\phi_{\text{flat\_Earth}}$ and to the height model of the Earth surface $\phi_{\text{topo}}$. $\phi_{\text{path}}$ and $\phi_{\text{noise}}$ capture perturbations from the atmosphere and noise. With the remaining so-called ‘‘phase-unwrapping’’ term $n2\pi$ (with $n\geq 1$), portions that exceed a complete wavelength are regarded. If the expected settlements are larger than the wavelength used, the evaluation becomes complex and erroneous. Further details on the technique used and the procedures (D-InSAR, PS-InSAR) for the evaluation of radar images can be found in the literature [3, 40].

Comprehensive analyses in [100] prove that an accuracy of less than 1.5 mm (standard deviation) can be reached with a sufficiently large sample. For the TerraSAR-X radar satellite the maximum repetition rate today, i.e., the time interval between two subsequent overflights, is 11 days. Thus, live monitoring of settlement data accompanying the excavation process is not possible yet. But, future satellite missions are already scheduled that will reduce the repetition rate down to 4 days by combining several satellites. The remarkable density of settlement information at so-called persistent scatterers (PS), i.e. at long-term stable natural or artificial radar reflectors, amounts to approximately 25,000 PS/km${}^{2}$ in inner-city regions.

2.6.3.3 Combination of Terrestrial and Extra-Terrestrial Techniques

If the advantages of both terrestrial and radar-interferometric methods are strategically combined, both performance and cost-effectiveness can be significantly increased. This also comprises the advantages of the satellite-based method in terms of gathering evidence. Without on-site installations, depending on the spatial resolution of the radar image on the ground, the monitoring region can be expanded almost at free will and without great additional expense. A potential combination of both methods is shown in Fig. 2.44.

Fig. 2.44

conceptual combination of terrestrial and radar-interferometric techniques in tunneling and its spatial coverage acc. to [19]

The fundamental principle is the reduction of terrestrial measurements in favor of radar-interferometric settlement monitoring. In the close range of the tunnel axis, terrestrial measurements are still indispensable at the time of the shield passage, since short measurement intervals are urgently needed for checking the alarm or threshold values. This is different in the long-distance range in space as well as in time, areal satellite-based methods are preferred which require some time for stochastic evaluation of several overflights. The best division of regions for terrestrial and radar-interferometric methods finally depends on the topology, the geology, the damage risk of existent buildings and potential compensation measures [98].

2.6.4 Data Handling and Visualization Techniques

Besides the actual settlement monitoring, visualization plays a decisive role [30]. Visualized in space and time, critical conditions such as torsional deformations when underpassing structures in parallel are recognized easier. Then, countermeasures can be taken more quickly and in a targeted manner. Numerous commercial data management systems offer closed solutions for visualization. This holistic and visual settings allow settlements to be interpreted significantly easier. Visualization supports different perspectives, provides fading of additional information and various zooming options for detailed viewing. Time-related data such as settlement data can be animated which offers a high degree of interoperability between users. At best, a three-dimensional presentation of the results in a virtual reality (VR) environment supports the aforementioned analysis options (Fig. 2.45).

Fig. 2.45

VR-Lab at the Ruhr-Universität Bochum, Germany

Virtual Reality offers the possibility of creating a realistic computer-generated three-dimensional and dynamic image of the reality. The generation takes place in real time and can be converted to the user’s viewing angle. To perceive the 3D effect, tools such as shutter glasses are required. A so-called flystick enables navigation. Both components can be tracked to account for the current position and viewing direction of the user in the computation of the image and perspective (Fig. 2.45).

If data is not only to be visualized but also made available for further analyses, e.g. for FE computations, integral product models on a BIM (Building Information Modeling) and IFC (Industry Foundation Classes) basis are needed [96]. Figure 2.46 exemplifies the visualization of structures, tunneling, settlement data and the soil during construction of the Wehrhahn line in Dusseldorf, Germany [30].

Fig. 2.46

Integral product model for visualization of soil (bore holes), ground water level, tunnel, tunnel boring machine, above ground infrastructure and settlement data obtained from radar interferometry [96]

2.6.5 Case Study: Wehrhahn line in Dusseldorf

The Earth-observation TerraSAR-X satellite of the German Aerospace Center (DLR) was launched in June 2007 to provide high-quality radar images from an altitude of 514 km. In the best available mode (Spotlight) the spatial resolution is about 1 $\times$ 1 m [28]. However, in the region of interest (Fig. 2.47), the tunnel construction site in Dusseldorf, Germany [30], another mode (Stripmap) with a resolution up to 3$\times$3 m was used.

Fig. 2.47

Radar-Image and tunneling axis (Dusseldorf, Germany) [99]

Results of displacements monitoring

To monitor displacements of existent infrastructures induced by tunneling a set of 16 TerraSAR-X images are evaluated, gaining already high density of persistent scatterers. A block of buildings near the starting shaft (Fig. 2.48 and 2.49) illustrates the settlement effects in a very clear way. It is especially appropriate, as the tunnel boring machine undergoes the buildings with only a small overburden between tunnel roof and existent foundations. Moreover, extended initial ground injections are arranged here to ‘‘prestress’’ the remaining ground and compensate subsequent settlements.

Fig. 2.48

Tunnel lining and region of compensating injections [99]

Fig. 2.49

Distribution of persistent scatterer along with displacements after eight months [99]

Results of uplift monitoring

To monitor the process of intended uplift by injections and the following settlements a conventional rubber tube leveling system was established at the foundations of the buildings close to the tunnel. The terrestrial data is used to verify and calibrate the satellite data in space and time. For this purpose terrestrial and PS measuring points are geo-referenced in identical coordinate systems and superimposed on the 3D terrestrial laser scan model of the intra-urban area (Fig. 2.49) including positions on roofs, facades and the ground surface.

Figure 2.50 shows a representative time-series of displacements obtained from PS measurements compared to terrestrial values close to the PS points. All values are related to initial values prior to the tunneling workout to ensure an overall identical basis. The vertical ground movements derived from the PS-InSAR technique correspond very well to the terrestrial values. This especially holds true, if the very small extents of movements in a millimeter range are taken into account as well as certain inevitable local differences in the single points. Figure 2.50 clearly illustrates the intended initial uplift of the injections and its compensating effect on the subsequent settlements. Thus, an almost unaffected state of the buildings is fulfilled. It should be noted that the displacements measured by the satellite are given in line of sight (LOS). They have to be converted with the angle of incidence to end up with purely vertical displacements that are comparable to the terrestrial measurements on ground. However, an exact evaluation of error rates is still in progress.

Fig. 2.50

Comparison of time-series of terrestrial determined displacements (solid lines) and satellite determined displacements (dashed lines) during compensating injections and shield tunneling crossing date [99]