Simulation of Stationary Gaussian Random Fields with a Gneiting Spatio-Temporal Covariance

Abstract

The nonseparable Gneiting covariance has become a standard to model spatio-temporal random fields. Its definition relies on a completely monotone function associated with the spatial structure and a conditionally negative semidefinite function associated with the temporal structure. This work addresses the problem of simulating stationary Gaussian random fields with a Gneiting-type covariance. Two algorithms, in which the simulated field is obtained through a combination of cosine waves are presented and illustrated with synthetic examples. In the first algorithm, the temporal frequency is defined on the basis of a temporal random field with stationary Gaussian increments, whereas in the second algorithm the temporal frequency is drawn from the spectral measure of the covariance conditioned to the spatial frequency. Both algorithms perfectly reproduce the correlation structure with minimal computational cost and memory footprint.

1 Introduction

The modeling, prediction and simulation of stationary random fields defined on Euclidean spaces crossed with the time axis, $\mathbb {R}^k \times \mathbb {R}$ with, in general, $k=2$ or 3, is widespread in hydrology, environment, climate, ecology and epidemiology applications. The representation of their correlation structure via traditional covariance models in $\mathbb {R}^{k+1}$ is often unsuitable to capture space-time interactions, reason for which specific models need to be developed. One of these, the Gneiting covariance, is widely used in climate studies due to its versatility, and is defined as

$$\begin{aligned} C(\boldsymbol{h},u) = \frac{\sigma ^2}{\bigl (1+\gamma (u)\bigr )^{k/2}} \, \varphi \left( \dfrac{|\boldsymbol{h} |^2}{1 + \gamma (u)} \right) , \qquad \boldsymbol{h} \in \mathbb {R}^k, \, u \in \mathbb {R}, \end{aligned}$$

(1)

where $\sigma >0$, $\gamma$ is a variogram (i.e., a conditionally negative semidefinite function) on $\mathbb {R}$ and $\varphi$ is a completely monotone function on $\mathbb {R}_+$. A subclass originally proposed by Gneiting in [1] is obtained by considering a variogram $\gamma$ of the form $\gamma (u) = \psi (u^2) -1$, where $\psi$ is a Bernstein function, i.e., a positive primitive of a completely monotone function. The general formulation (1), in which $\gamma$ can be any variogram on $\mathbb {R}$, is due to Zastavnyi and Porcu in [2]. Hereinafter, without loss of generality, we assume $\sigma =1$ and $\varphi (0)=1$.

This work deals with the problem of simulating a stationary Gaussian random field with zero mean and Gneiting covariance on a (structured or unstructured) grid of $\mathbb {R}^k \times \mathbb {R}$. The following section presents some theoretical results, which will be used in Sects. 3 and 4 to design two simulation algorithms, which will be illustrated on synthetic examples. Concluding remarks follow in Sect. 5.

2 Theoretical Results

The completely monotone function $\varphi$ can be written as a nonnegative mixture of decreasing exponential functions on $\mathbb {R}_+$:

$$\begin{aligned} \varphi (t) = \varphi (0) \, \int _{\mathbb {R}_+} \exp ( - r \, t) \, \mu (dr) , \qquad t \in \mathbb {R}_+, \end{aligned}$$

(2)

where $\mu$ is a probability measure. Also, the continuous Fourier transform of a squared exponential function in $\mathbb {R}^k$ is another squared exponential function:

$$\begin{aligned} \int _{\mathbb {R}^k} \cos \bigl ( \langle \boldsymbol{\omega } , \boldsymbol{h} \rangle \bigr ) \, \exp \bigl ( - a \, \vert \boldsymbol{\omega } |^2 \bigr ) d \boldsymbol{\omega } = \left( \frac{\pi }{a} \right) ^{k/2} \, \exp \left( - \frac{|\boldsymbol{h} |^2}{4 a} \right) \qquad \boldsymbol{h} \in \mathbb {R}^k , \, a > 0, \end{aligned}$$

(3)

where $\langle \cdot , \cdot \rangle$ stands for the usual scalar product in $\mathbb {R}^k$.

Proposition 1

By combining Eqs. (2) and (3), one can rewrite the Gneiting covariance (1) as follows:

$$\begin{aligned} C (\boldsymbol{h},u) = \int _\mathbb {R} \int _{\mathbb {R}^k} \cos \bigl ( \sqrt{2 r} \, \langle \boldsymbol{\omega } , \boldsymbol{h} \rangle \bigr ) \, \exp \left( - \frac{\gamma (u)}{2} \, |\boldsymbol{\omega } |^2 \right) \, g^{\phantom {\vert }}_{I_k} ( \boldsymbol{\omega }) \, d \boldsymbol{\omega } \, \mu (dr), \end{aligned}$$

(4)

with $I_k$ the identity matrix of order k and $g^{\phantom {\vert }}_{I_k}$ the probability density of a k-dimensional Gaussian random vector with zero mean and covariance matrix $I_k$.

The mappings $\boldsymbol{h} \, \mapsto \, \cos \bigl ( \sqrt{2 r} \, \langle \boldsymbol{\omega } , \boldsymbol{h} \rangle \bigr )$ and $u \, \mapsto \, \exp \bigl ( - \gamma (u) \, |\boldsymbol{\omega } |^2 / 2 \bigr )$ are covariances functions in $\mathbb {R}^k$ and $\mathbb {R}$, respectively. Their product is therefore a covariance function in $\mathbb {R}^k \times \mathbb {R}$, and so is $C (\boldsymbol{h},u)$ as a positive mixture of covariances functions in $\mathbb {R}^k \times \mathbb {R}$. This result proves that every member of the Gneiting class (1) is a valid space-time covariance. In particular C is a positive semidefinite function in $\mathbb {R}^k \times \mathbb {R}$.

Proposition 2

One can further decompose the Gneiting covariance as follows:

$$\begin{aligned} C (\boldsymbol{h},u) = \mathbb {E} \left\{ \cos \left( \sqrt{2 R} \, \langle \boldsymbol{\varOmega } , \boldsymbol{h} \rangle + Y \, \sqrt{ \gamma (u) } \, |\boldsymbol{\varOmega } |\right) \right\} , \end{aligned}$$

(5)

where $\mathbb {E} \{ \cdot \}$ the mathematical expectation, R a nonnegative random variable with distribution $\mu$, Y a standard normal random variable, $\boldsymbol{\varOmega }$ a k-dimensional standardized Gaussian random vector, and where $R,Y,\boldsymbol{\varOmega }$ are independent.

Proof

One uses (3) to write the squared exponential function in (4) as a Fourier transform on $\mathbb {R}$:

$$\begin{aligned} C (\boldsymbol{h},u) = \int _\mathbb {R} \int _{\mathbb {R}^k} \int _\mathbb {R} \cos \bigl ( \sqrt{2 r} \, \langle \boldsymbol{\omega } , \boldsymbol{h} \rangle \bigr ) \, \cos \bigl ( y \sqrt{ \gamma (u)} \, |\boldsymbol{\omega } |\bigr )\, g^{\phantom {\vert }}_1 (y) \, g^{\phantom {\vert }}_{I_k} ( \boldsymbol{\omega } ) \, d y \, d \boldsymbol{\omega } \, \mu (dr), \end{aligned}$$

where $g^{\phantom {\vert }}_1$ is the standard normal univariate probability density function. Owing to the parity of this function and to the product-to-sum trigonometric identity, this expression simplifies into

$$\begin{aligned} C (\boldsymbol{h},u) = \int _\mathbb {R} \int _{\mathbb {R}^k} \int _\mathbb {R} \cos \bigl ( \sqrt{2 r} \, \langle \boldsymbol{\omega } , \boldsymbol{h} \rangle + y \sqrt{ \gamma (u)} \, |\boldsymbol{\omega } |\bigr ) \, g^{\phantom {\vert }}_1 (y) \, g^{\phantom {\vert }}_{I_k} ( \boldsymbol{\omega }) \, d y \, d \boldsymbol{\omega } \, \mu (dr), \end{aligned}$$

which yields the claim.

3 A Discrete-in-Time and Continuous-in-Space Substitution Algorithm

Consider a space-time cosine wave of the following form:

$$\begin{aligned} Z (\boldsymbol{x},t) = \sqrt{2} \, \cos \left( \sqrt{2 R} \, \langle \boldsymbol{\varOmega } , \boldsymbol{x} \rangle + W (t) \, \frac{|\boldsymbol{\varOmega } |}{\sqrt{2}} + \varPhi \right) , \qquad \boldsymbol{x} \in \mathbb {R}^k, t \in \mathbb {R}, \end{aligned}$$

(6)

where

• R and $\boldsymbol{\varOmega }$ are a random variable and a random vector as defined in (5);

• $\{ W(t): t \in \mathbb {R} \}$ is a strictly intrinsic random field with variogram $\gamma$ and Gaussian increments;

• $\varPhi$ is a uniform random variable on $]0,2\pi [$;

• $R, \boldsymbol{\varOmega }, W$ and $\varPhi$ are independent.

Because $\varPhi$ is uniform on $]0,2\pi [$ and is independent of $( R, \boldsymbol{\varOmega }, W)$, this cosine wave is centered. Moreover, the covariance between $Z(\boldsymbol{x}+\boldsymbol{h},t+u)$ and $Z(\boldsymbol{x},t)$ is found to be equal to the expectation in (5), that is, $C(\boldsymbol{h},u)$ (see [3]). The random field in (6) is a particular case of substitution random field, consisting of the composition of a stationary coding process on $\mathbb {R}$ and an intrinsic directing function on $\mathbb {R}^k \times \mathbb {R}$ (see [4]).

To obtain an approximately Gaussian random field with zero mean and Gneiting covariance, one can (i) multiply the cosine by a Rayleigh random variable with scale parameter $2^{-1/2}$, which makes the marginal distribution of $Z(\boldsymbol{x},t)$ be standard Gaussian, and (ii) sum and standardize many of such independent cosine waves, so that the finite-dimensional distributions of $Z(\boldsymbol{x},t)$ become approximately multivariate Gaussian due to the central limit theorem. The simulated random field thus takes the form:

$$\begin{aligned} Z (\boldsymbol{x},t) = \sum _{j=1}^p \sqrt{ \frac{ - 2 \ln U_j}{p}} \, \cos \left( \sqrt{2 R_j} \, \langle \boldsymbol{\varOmega }_j , \boldsymbol{x} \rangle + W_j (t) \, \frac{|\boldsymbol{\varOmega }_j |}{\sqrt{2}} + \varPhi _j \right) , \end{aligned}$$

(7)

where p is a large integer, $\bigl \{ ( R_j, \boldsymbol{\varOmega }_j, W_j, \varPhi _j ): j=1,...,p \bigr \}$ are independent copies of $( R, \boldsymbol{\varOmega }, W, \varPhi )$, and $\{ U_j: j=1,...,p \}$ are independent random variables uniformly distributed on ]0, 1[ and are independent of $\bigl \{ ( R_j, \boldsymbol{\varOmega }_j, W_j, \varPhi _j ): j=1,...,p \bigr \}$.

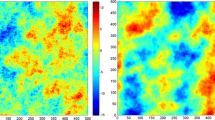
As an illustration, consider the simulation of a random field on a regular grid of $\mathbb {R}^1 \times \mathbb {R}$ with $500 \times 500$ nodes and mesh $1 \times 0.2$, with the following parameters:

• $k=1$;

• $\varphi (r) = \exp ( - 0.001 r)$

• $\gamma (u) = \sqrt{1 + |u |} - 1$;

• $p=10, 100$ or 1000.

The intrinsic random field W is simulated by using the covariance matrix decomposition algorithm with the nonstationary covariance function $(t,t^\prime ) \mapsto \gamma (t) + \gamma (t^\prime ) - \gamma (t^\prime -t)$. The simulation obtained with $p = 10$ cosine waves exhibits an apparent periodicity in space, which indicates that the central limit approximation is poor, which is no longer the case when using 100 or more cosine waves (Fig. 1, left). In contrast, since the simulated process W is ergodic, the time variations are well reproduced, irrespective of the number of cosine waves. Note that the simulated random field has a Gaussian spatial covariance and a gamma temporal covariance with parameter 0.5, hence it is smooth in space but not in time.

Fig. 1

Simulation of a random field with Gneiting covariance function (with an exponential function for $\varphi$ and a square root for $\gamma$) using 10 (top), 100 (center) and 1000 (bottom) cosine waves. Left: substitution algorithm. Right: spectral algorithm

4 A Fully Continuous Spectral Algorithm

The continuous spectral method relies on the fact that the continuous covariance C is the Fourier transform of a symmetric probability measure F on $\mathbb {R}^k \times \mathbb {R}$. Let $(\boldsymbol{\varOmega }, {\textrm{T}})$ be a spectral vector distributed according to F, and $\varPhi$ a random phase uniform on $]0,2 \pi [$ and independent of $(\boldsymbol{\varOmega }, {\textrm{T}})$. Then, the random field defined by

$$\begin{aligned} Z(\boldsymbol{x},t) = \sqrt{2} \cos \bigl ( \langle \boldsymbol{\varOmega } , \boldsymbol{x} \rangle + {\textrm{T}} t + \varPhi \bigr ), \qquad ( \boldsymbol{x},t) \in \mathbb {R}^k \times \mathbb {R}, \end{aligned}$$

(8)

is second-order stationary with covariance C. A standard approach for simulating the spectral vector is to simulate at first the spatial component $\boldsymbol{\varOmega }$, then the temporal component ${\textrm{T}}$ given $\boldsymbol{\varOmega }$, which requires explicitly knowing the spectral measure. For instance, consider the covariance function with $\varphi (r)=\exp (-a r)$ ($a>0$) and $\gamma (u)=\sqrt{1+|u |}-1$. In this case, it can be shown (see [3]) that $\boldsymbol{\varOmega }$ is a Gaussian random vector with independent components and that ${\textrm{T}}$ given $\boldsymbol{\varOmega } = \boldsymbol{\omega }$ follows a Cauchy distribution whose scale parameter follows an inverse Gaussian distribution, all these distributions being simulatable.

In practice, the multiplication of the cosine wave (8) by a Rayleigh random variable and the independent replication technique of (7) provide a random field with Gaussian marginal distributions and approximately multivariate Gaussian finite-dimensional distributions. Figure 1 (right) displays realizations obtained by using between $p = 10$ and $p = 1000$ cosine waves. The spatial variations are similar to those observed with the substitution algorithm. However, the temporal variations differ when using few cosine waves, exhibiting a smooth and periodic behavior when $p = 10$ or $p = 100$. This suggests that the convergence to a multivariate-Gaussian distribution in time is slower with the spectral algorithm than with the substitution algorithm.

5 Concluding Remarks

The two presented approaches construct the simulated random field as a weighted sum of cosine waves with random frequencies and phases. Their main difference lies in the way to simulate the temporal frequency: from its distribution conditional to the spatial frequency (spectral approach), or from an intrinsic time-dependent random field (substitution approach). Both algorithms have a computational complexity in $\mathcal {O}(n)$, considerably cheaper than generic algorithms such as the covariance matrix decomposition and sequential algorithms, are parallelizable and require minimal memory storage space, which makes them affordable for large-scale problems. The substitution approach is general and only requires the knowledge of the temporal variogram $\gamma$ and the probability measure $\mu$ specifying the completely monotone function $\varphi$ (2) associated with the spatial structure. In contrast, the spectral approach is more specific, as it also requires the knowledge of the time frequency distribution conditional to the spatial frequency, which has to be solved on a case-by-case basis.