Transfer of a Biological Fluid Through a Porous Wall of a Capillary

Abstract

The treatise proposes a model of biological fluid transfer in a dedicated macropore with microporous walls. The distribution of concentrations and velocity studies in the capillary wall for two flow regimes—convective and diffusive. The largest impact on the redistribution of concentration between the capillary volume and its porous wall is made by Darcy number and correlation of diffusion coefficients and concentration expansion. The velocity in the interface vicinity increases with rising pressure in the capillary volume or under decreasing porosity or without consideration of the concentration expansion.

1 Introduction

Contemporary medicine widely implements agents for tissue culture, delivery systems for pharmaceuticals, implants, bandages, arterial conduits, etc. The efficacy of all synthesized materials depends on their structure, including the structure of the pore space, which largely controls the kinetics of biochemical processes. For example, an implant should possess a strictly determined pore size promoting the formation of blood vessels during tissue growth. The structure of biological porous media is multiscale. Along with macroscopic pores, there are a lot of capillaries. Pore walls, in turn, consist of several layers, each of which has its own structure. The properties of the surfaces of pores and capillaries also affect the flow of biological fluids.

The main biological fluids of a person include blood, tissue fluid and lymph. The first performs mainly a transport function. Essentials for life enter the cells through the tissue fluid from the blood into the cells. The main function of the third fluid is protective. Lymph destroys pathogens and ensures the return of tissue fluid into the bloodstream. The blood vessels through which blood flows from the heart form the arterial system, and the vessels that collect blood and carry it to the heart form the venous system. The metabolism between the blood and body tissues is carried out using capillaries that penetrate the organs and most tissues. The main functions of the blood and circulatory system are to connect organs and cells to ensure their vital functions—in the delivery of oxygen, nutrients, hormones, excretion of decomposition products, maintaining a constant body temperature, and protection from harmful microbes [1, 2]. All this suggests the need to study the flow of biological fluids in the system of vessels and capillaries, taking into account the features of the structure and rheological properties and the development of appropriate models [3]. The rheological properties of blood are mainly due to the processes of hydrodynamic interaction of erythrocytes with plasma, which contribute to the formation and decay of aggregates, rotation and deformation of red blood cells, their redistribution, and the corresponding orientation in the flow [4]. Blood is a heterogeneous and multiphase physical and chemical system. It can be represented as a suspension and non-Newtonian fluid with complex rheological properties. In addition to modeling blood flow in large blood vessels [2, 4,5,6,7,8] there are a number of works in the literature in which the flow in capillaries is simulated.

For example, work [9] has analyzed three variants of mathematical models describing the flow of a viscous incompressible fluid in a long cylindrical capillary with its internal surface covered by a permeable porous layer. The authors have shown that for thin weakly permeable porous layers on the capillary walls, the Brinkman model is not applicable; one just can use the Navier slip condition. If the porous layer is thick and/or is weakly permeable, it is not allowed to neglect the effect of the flow in it on the total fluid flow rate through the capillary, and an adequate description of the filtration process should be made using the Brinkman model.

In [10, 11], the authors have studied the blood flow through porous blood vessels taking into account an electromagnetic field. They have suggested a blood flow model in an artery with porous walls within the model of a non-Newtonian fluid in the presence of electromagnetic field. In these works, the viscosity of the non-Newtonian fluid depended on the temperature and magnetic field and was calculated by the models of Reynolds and Vogel or was assumed to be constant.

There are a lot of works devoted to modeling of blood flow in capillaries [12,13,14]. The authors investigate the influence of diverse parameters on the fluid motion in capillaries: vessel curvature [15], capillary radius and shape [16,17,18], dynamics of oxygen transportation [19], hemodynamics of vascular prostheses and implants [20, 21].

Important applications of biomedical systems, such as biological tissues, require taking into account the flow, heat and mass exchange through a porous medium [22]. The theory of transfer in a porous medium on the basis of various models, such as Darcy-Brinkman model of momentum transfer and local thermal equilibrium for energy transfer, were analyzed by the authors and can be particularly useful in describing different biological applications.

In general case, biological fluids possess specific rheological properties. As a rule, biological fluids are non-Newtonian fluids that are described by various rheological models. In the literature, models of viscoelastic, viscoplastic, pseudo-plastic and dilatant fluids are widely used. All the models, with due consideration of complex rheology, are non-linear. The non-linear effects also manifest when accounting the dependence of properties (for instance, viscosity) on concentration.

Current work suggests a model of biological fluid transfer in a selected macropore with microporous walls. Unlike [10, 11], we assume isothermal conditions; however, we assume some the state equations for pressure in the fluid to be differential [23, 24], which yields a non-linear coupled model.

2 General Equations

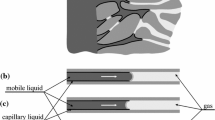
Let us formulate the problem on the transfer of a biological fluid (or a pharmaceutical) in a selected cylindrical macropore with radius $R_{1}$ having microporous walls (Fig. 1). Area 1 is the macropore, area 2 is the porous layer with thickness $\delta = R_{2} - R_{1}$.

Fig. 1

Cylindrical pore with radius R₁ having porous walls

To construct the model we use the continuity equation:

$$ \frac{\partial \rho }{\partial t} + \nabla \cdot \left( {\rho {\mathbf{v}}} \right) = 0, $$

(1)

balance equation for species

$$ \rho \left( {\frac{{\partial C_{k} }}{\partial t} + {\mathbf{v}}\nabla C_{k} } \right) = - \nabla \cdot {\mathbf{J}}_{k} , $$

(2)

and motion equation

$$ \rho \frac{{\partial {\mathbf{v}}}}{\partial t} + \rho {\mathbf{v}}\nabla \left( {\mathbf{v}} \right) = - \nabla \cdot {\varvec{\upsigma}} + \rho {\mathbf{F}}, $$

(3)

where ρ is the density, ${\mathbf{v}}$ is the velocity of centre of mass; C_k—species (component) concentrations; ${\mathbf{J}}_{k}$ is diffusion flux of this component; σ is stress tensor; F is the mass force vector; $\nabla \ldots \equiv grad \ldots$; $\nabla \cdot \ldots \equiv div \ldots$

We will describe the flow in the macropore (area 1) using Navier-Stokes equations . The microporous medium (area 2) will be modeled as Brinkman medium . In a first approximation, the biological fluid is assumed incompressible. Navier-Stokes equations follows from (3) when

$$ \sigma_{ij} = - P\delta_{ij} + 2\mu e_{ij} , $$

(4)

and ${\mathbf{F}} = {\mathbf{F}}_{1} = - \frac{1}{\rho }\nabla \left( {gz} \right)$. Here p is hydrodynamic pressure and $e_{ij}$ is the tensor of strain rates,

$$ e_{ij} = \frac{1}{2}\left( {\frac{{\partial V_{i} }}{{\partial x_{j} }} + \frac{{\partial V_{j} }}{{\partial x_{i} }}} \right), $$

$V_{i}$ are components of the velocity vector.

Brinkman medium appears when we assume

$$ {\mathbf{F}} = {\mathbf{F}}_{ 1} + {\mathbf{F}}_{ 2} , $$

(5)

where ${\mathbf{F}}_{2}$ is the force of internal friction depending on filtration velocity, w. Then ${\mathbf{v}} = {\mathbf{w}}/a,\;a = S_{p} /S$, and $S_{p}$ is the area occupied by pores in the section $S$.

If the fluid is incompressible (which is usually accepted for slow flows), instead continuity equations (1) will remain:

$$ \nabla \cdot {\mathbf{v}}_{i} = 0;\quad i = 1 , 2. $$

(6)

As a result we obtain for area inside the capillary:

$$ 0 < r < R_{1} :\quad \rho_{1} \left( {\frac{{\partial C_{k} }}{\partial t} + {\mathbf{v}}_{1} \nabla C_{k} } \right) = - \nabla \cdot {\mathbf{J}}_{k} , $$

(7)

$$ \rho_{1} \left( {\frac{{\partial {\mathbf{v}}_{1} }}{\partial t} + {\mathbf{v}}_{1} \nabla {\mathbf{v}}_{1} } \right) = - \nabla p_{1} + \rho_{1} gz + \nabla \cdot \left( {\mu_{1} \nabla {\mathbf{v}}_{1} } \right), $$

(8)

and for the porous walls:

$$ R_{1} < r < R_{2} :\quad \rho_{2} \left( {\frac{{\partial C_{k} }}{\partial t} + {\mathbf{v}}_{2} \nabla C_{k} } \right) = - \nabla \cdot {\mathbf{J}}_{k} , $$

(9)

$$ \rho_{2} \left( {\frac{{\partial {\mathbf{v}}_{2} }}{\partial t} + {\mathbf{v}}_{2} \nabla {\mathbf{v}}_{2} } \right) = - \nabla p_{2} + \rho_{2} gz + \left( {\nabla \cdot \left( {\mu_{2} \nabla {\mathbf{v}}_{2} } \right) - \mu_{2}^{/} m\frac{{{\mathbf{v}}_{2} }}{{k_{f} }}} \right). $$

(10)

Here ${\mathbf{v}}_{1}$, ${\mathbf{v}}_{2}$, $\rho_{1}$, $\rho_{2}$ are the vectors of velocities and densities of the liquid in areas 1 and 2, $C_{k}$ is the concentration of the k-th component, ${\mathbf{J}}_{k} = - D_{k} \rho_{i} \nabla C_{k}$ is the diffusion flux of the k-th component; $P_{1}$, $P_{2}$, $\mu_{1}$, $\mu_{2}$ are the pressure and viscosity of the fluid in areas 1 and 2, $\mu_{2}^{/}$ is the viscosity in the Darcy’s law, in general case it differs from $\mu_{2}$; $g$ is the force of gravity; $k_{f}$ is the permeability of the porous medium; $m$ is the porosity of pore walls.

In the case of slow (crawl) flow, the second summands in the left brackets of the motion equations for porous walls can be neglected.

We should add the state equation connecting the pressure with temperature and fluid composition. For constant temperature, we can write [23, 25]

$$ dp = - \rho \beta_{T}^{ - 1} d\gamma + \sum\limits_{k = 1}^{n} {p_{k} dC_{k} } $$

(11)

where $p_{k} = \alpha_{k} \beta_{T}^{ - 1}$, $\alpha_{k}$ is concentration expansion coefficients, $\beta_{T}$ is isothermal compressibility coefficient, $\beta_{T}^{ - 1} = K$; K is bulk module for fluid. Then for incompressible fluid with constant properties for each area we have

$$ p_{2} - p_{20} = 3K\alpha \left( {C_{2} - C_{20} } \right)\quad {\text{and}}\;\;p_{1} - p_{10} = 3K\alpha \left( {C_{1} - C_{10} } \right), $$

(12)

where C₁₀ and C₂₀ is preset zero approximation, $p_{10}$ and $p_{20}$—is initial pressures values in areas.

3 Stationary Model

From (7)–(10) we obtain stationary model for individual pore The hydrodynamic part of the problem will include equations:

$$ 0 < r < R_{1} :\quad \rho_{1} V_{1} \frac{{dV_{1} }}{dr} = - \frac{{dp_{1} }}{dr} + \frac{1}{r}\frac{d}{dr}\left( {r\mu_{1} \left( {C_{1} } \right)\frac{{dV_{1} }}{dr}} \right), $$

(13)

$$ R_{1} < r < R_{2} :\quad \frac{{dp_{2} }}{dr} - \left( {\frac{1}{r}\frac{d}{dr}\left( {r\,\mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}} \right) - \mu_{2}^{/} \left( {C_{2} } \right)m\frac{{V_{2} }}{{k_{f} }}} \right) = 0, $$

(14)

where V_k, k = 1,2 are radial components of velocity for areas.

The boundary conditions for the hydrodynamic part of the problem will be as follow. In the point $r = 0$ we have the symmetry condition

$$ V_{1} = 0. $$

(15)

In the interface between two areas, mass velocities and stress tensor components are equal

$$ r = R_{1} :\quad \rho_{1} V_{1} = m\rho_{2} V_{2} ,\;\; - p_{1} + \mu_{1} \left( {C_{1} } \right)\frac{{dV_{1} }}{dr} = m\left( { - p_{2} + \mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}} \right). $$

(16)

We can assume that the outer wall of the capillary ($r = R_{2}$) is free of load, on

$$ \sigma_{rr} = - p_{2} + \mu_{2} \frac{{dV_{2} }}{dr} = 0 $$

(17)

or (other case)

$$ V_{2} = 0. $$

(18)

The viscosities linearly depend on concentration:

$$ \mu_{1} \left( {C_{1} } \right) = \mu_{10} + \mu_{11} C_{1} ,\quad \mu_{2} \left( {C_{2} } \right) = \mu_{20} + \mu_{21} C_{2} . $$

(19)

For the diffusion part of the problem, we have:

$$ 0 < r < R_{1} :\quad \rho_{1} V_{1} \frac{{dC_{1} }}{dr} = \frac{1}{r}\frac{d}{dr}\left( {D_{1} \rho_{1} r\frac{{dC_{1} }}{dr}} \right), $$

(20)

$$ R_{1} < r < R_{2} :\quad \rho_{2} V_{2} \frac{{dC_{2} }}{dr} = \frac{1}{r}\frac{d}{dr}\left( {D_{2} \rho_{2} r\frac{{dC_{2} }}{dr}} \right), $$

(21)

$$ r = 0:\quad \frac{{dC_{1} }}{dr} = 0, $$

(22)

$$ r = R_{1} :\quad C_{1} = mC_{2} ,\;\;\rho_{1} \left[ {D_{1} \frac{{dC_{1} }}{dr} - V_{1} C_{1} } \right] = \rho_{2} m\left[ {D_{2} \frac{{dC_{2} }}{dr} - V_{2} C_{2} } \right], $$

(23)

$$ r = R_{2} :\quad \rho_{2} \left( {D_{2} \frac{{dC_{2} }}{dr} - V_{2} C_{2} } \right) = \varOmega , $$

(24)

where $D_{1}$, $D_{2}$ are the diffusion coefficients in areas 1 and 2.

The condition (22) is symmetry condition; first of (23) follows from chemical potential continuity, second of (23) is the equality of the total mass flows; condition (24) contains the mass sink on the outer wall of the capillary $\Omega$.

Taking into account the connection between pressure and concentration (12), from (13), (14), (16), (17) we obtain

$$ \begin{aligned} & \rho_{1} V_{1} \frac{{dV_{1} }}{dr} = - 3K\alpha \frac{{dC_{1} }}{dr} + \frac{1}{r}\frac{d}{dr}\left( {r\mu_{1} \left( {C_{1} } \right)\frac{{dV_{1} }}{dr}} \right); \\ & 3K\alpha \frac{{dC_{2} }}{dr} - \left( {\frac{1}{r}\frac{d}{dr}\left( {r\mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}} \right) - \mu_{2}^{/} \left( {C_{2} } \right)m\frac{{V_{2} }}{{k_{f} }}} \right) = 0; \\ & - \left( {3K\alpha \left( {C_{1} - C_{10} } \right) + p_{10} } \right) + \mu_{1} \left( {C_{1} } \right)\frac{{dV_{1} }}{dr} \\ & \quad = m\left( { - \left( {3K\alpha \left( {C_{2} - C_{20} } \right) + p_{20} } \right) + \mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}} \right); \\ & \sigma_{rr} = - \left( {3K\alpha \left( {C_{2} - C_{20} } \right) + p_{20} } \right) + \mu \frac{{dV_{2} }}{dr} = 0. \\ \end{aligned} $$

In this model we assumed that viscosity of fluid and diffusion coefficients in pore and in porous wall are different, that connect with special structure of porous space affecting the fluid mobility. These problem is coupling in general case.

4 Special Case

The simplest stationary diffusion model for individual pore can be analyzed for the case when the pressure gradient along the macro pores is given, and the fluid composition in pore is fixed (we neglect the gravitational force):

$$ \nabla p_{1} = \omega = const,\quad C_{1} = C_{10} . $$

(25)

Because in interface $\rho_{1} V_{1} = m\rho_{2} V_{2}$ and the pressure is proportional to concentration, then we do not mistake if assume:

$$ \nabla p_{1} = const = \beta \omega \sim \nabla p_{2} , $$

(26)

where $\omega ,\,\beta$ is some constants. In this case the hydrodynamical part of the problem turns to

$$ \omega - \frac{1}{r}\frac{d}{dr}\left( {r\mu_{1} \left( {C_{10} } \right)\frac{{dV_{1} }}{dr}} \right) = 0; $$

(27)

$$ \omega \beta - \left( {\frac{1}{r}\frac{d}{dr}\left( {r\mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}} \right) - \frac{{V_{2} }}{{k_{f} }}} \right) = 0; $$

(28)

$$ r = 0:\quad V_{1} = 0;\;\;r = R_{2} ;\;\;V_{2} = 0; $$

(29)

$$ r = R_{1} :\quad \rho_{1} V_{1} = m\rho_{2} V_{2} ;\;\;\mu_{1} \left( {C_{i0} } \right)\frac{{dV_{1} }}{dr} = m\mu_{2} \left( {C_{2} } \right)\frac{{dV_{2} }}{dr}. $$

(30)

For the case of constant viscosity, the exact analytical solution of this problem is presented in [26].

Diffusion part of the problem takes a place only for the area $R_{1} \le r \le R_{2}$:

$$ \rho_{2} V_{r2} \left( {r;C_{10} ,C_{2} ,m,\omega } \right)\frac{{dC_{2} }}{dr} = \frac{1}{r}\frac{d}{dr}\left( {D_{2} \rho_{2} r\frac{{dC_{2} }}{dr}} \right); $$

$$ r = R_{1} :\quad C_{10} = mC_{2} ; $$

$$ r = R_{2} :\quad C_{2} = 0. $$

We assume that velocity distribution in the walls is given and does not depend on concentration. It is obviously, when the velocity is equals to zero, and diffusion coefficient is constant value, we come to concentration distribution coinciding with the exact analytical solution (Fig. 2a, b—lines 1):

Fig. 2

Concentration distribution in the wall of pore (a) for different diffusion coefficients (b). $D_{20} = 10^{ - 3}$ μm/s, 1—$\alpha_{p2} = 0$; 2—$\alpha_{p2} = 6$; 3—$\alpha_{p2} = 10$

$$ C_{2} = \frac{{C_{10} }}{m}\frac{{\ln \left( {r/R_{2} } \right)}}{{\ln \left( {R_{1} /R_{2} } \right)}}. $$

This solution does not contain density and diffusion coefficient.

If diffusion coefficient depends on space coordinate (that could be connected with the change of pore structure, for example, using the equation $D_{2} = D_{20} /\left( {1 + \alpha_{p2} \left( {r - R_{1} } \right)} \right)$, then concentration distribution changes (2 and 3 curves correspondingly) in this figure.

The positive value of given filtration velocity effects on concentration distribution similarly (Fig. 3). However, the type of the velocity distribution is not essential concentration (Fig. 4).

Fig. 3

Concentration distribution for given filtration rate. 1—$V_{2} = 0.1$; 2—$V_{2} = 0$; 3—$V_{2} = 0.2$ μm/s, $D_{20} = 10^{ - 3}$ μm/s

Fig. 4

Concentration distribution (a) and liquid velocity in pore wall (b). Black line—is exact analytical solution for $V_{2} = 0$; the colors of the lines to the left correspond to colors of the lines to the right. $D_{20} = 10^{ - 3}$ μm/s

The concentration distribution in Fig. 4b is given for the velocity functions $V_{2} \left( r \right)$, presented in the Fig. 4a. The change of the velocity with the coordinate could be connects with the complex structure of porous space, with structure of pore surface, with their specific tortuosity, the close pores availability leading to inhibition of concentration distribution along pore walls.

5 Dimensionless Variables and Parameters in Total Stationary Model

Let us introduce the following dimensionless variables:

$$ \xi = \frac{r}{{R_{2} }},\quad \overline{V}_{i} = \frac{{V_{i} }}{{\mu_{10} /\rho_{1} R_{2} }},\;\;\bar{p}_{i} = \frac{{p_{i} }}{{\mu_{10}^{2} /\rho_{1} R_{2}^{2} }}. $$

Then the equations and boundary conditions in dimensionless variables will be rewritten as

$$ 0 < \xi < 1 - \Delta :\quad \overline{V}_{r1} \frac{{d\overline{V}_{1} }}{d\xi } = - \frac{{d\bar{p}_{1} }}{d\xi } + \frac{1}{\xi }\frac{d}{d\xi }\left( {\xi \bar{\mu }_{1} \left( {C_{1} } \right)\frac{{d\overline{V}_{1} }}{d\xi }} \right), $$

(31)

$$ Pe_{D} \overline{V}_{1} \frac{{dC_{1} }}{d\xi } = \frac{1}{\xi }\frac{d}{d\xi }\left( {\xi \frac{{dC_{1} }}{d\xi }} \right), $$

(32)

$$ 1 - \Delta < \xi < 1:\quad Da\frac{{d\bar{p}_{2} }}{d\xi } - \left( {\frac{Da}{\xi }\frac{d}{d\xi }\left( {\xi \,\bar{\mu }_{2} \left( {C_{2} } \right)\frac{{d\overline{V}_{2} }}{d\xi }} \right) - \bar{\mu }_{2}^{/} m\left( {C_{2} } \right)\overline{V}_{2} } \right) = 0, $$

(33)

$$ Pe_{D} \overline{V}_{2} \frac{{dC_{2} }}{d\xi } = \overline{D} \frac{1}{\xi }\frac{d}{d\xi }\left( {\xi \frac{{dC_{2} }}{d\xi }} \right), $$

(34)

$$ \xi = 0:\quad \overline{V}_{1} = 0,\;\;\frac{{dC_{1} }}{d\xi } = 0, $$

(35)

$$ \xi = 1 - \Delta :\quad \overline{V}_{r1} = m\bar{\rho }\overline{V}_{r2} .\;\; - \bar{p}_{1} + \bar{\mu }_{1} \left( {C_{1} } \right)\frac{{d\overline{V}_{r1} }}{d\xi } = m\left( { - \bar{p}_{2} + \bar{\mu }_{2} \left( {C_{2} } \right)\frac{{d\overline{V}_{r2} }}{d\xi }} \right), $$

(36)

$$ C_{1} = mC_{2} ,\quad \frac{{dC_{1} }}{d\xi } - Pe_{D} \overline{V}_{1} C_{1} = m\bar{\rho }\left( {\overline{D} \frac{{dC_{2} }}{d\xi } - Pe_{D} \overline{V}_{2} C_{2} } \right), $$

(37)

$$ \xi = 1:\quad \bar{\mu }_{2} \frac{{d\overline{V}_{r2} }}{d\xi } = \bar{p}_{20} + K_{bez} \left( {C_{2} - C_{20} } \right), $$

(38)

$$ \overline{D} \frac{{dC_{2} }}{d\xi } - Pe\overline{V}_{2} C_{2} = \overline{\Omega } , $$

(39)

where $\bar{\mu }_{1} \left( {C_{1} } \right) = 1 + \alpha_{1} C_{1}$, $\bar{\mu }_{2} \left( {C_{2} } \right) = \beta + \alpha_{2} C_{2}$, $\bar{\mu }_{2}^{/} = \bar{\mu }_{2}$, $\bar{p}_{2} - \bar{p}_{20} = K_{bez} \left( {C_{2} - C_{20} } \right) \,$ and $\bar{p}_{1} - \bar{p}_{10} = K_{bez} \left( {C_{1} - C_{10} } \right) \,$.

Stationary model contains following dimensionless parameters:

$$ \begin{aligned} & Pe_{D} = \frac{{V_{*} R_{2} }}{{D_{1} }},\quad Da = \frac{{k_{f} }}{{R_{2}^{2} }},\;\;K_{bez} = \frac{{K\alpha R_{2}^{2} \rho_{1} }}{{\mu_{10}^{2} }},\;\;\overline{D} = \frac{{D_{2} }}{{D_{1} }},\;\;\Delta = \frac{\delta }{{R_{2} }}, \\ & \bar{\rho } = \frac{{\rho_{2} }}{{\rho_{1} }},\quad m,\;\;\alpha_{1} = \frac{{\mu_{11} }}{{\mu_{10} }},\;\;\alpha_{2} = \frac{{\mu_{21} }}{{\mu_{10} }},\;\;\beta = \frac{{\mu_{20} }}{{\mu_{10} }},\;\;\overline{\Omega } = \frac{{\varOmega R_{2} }}{{\rho_{2} D_{1} }}. \\ \end{aligned} $$

Diffusion Peclet number $Pe_{D}$ includes the velocity $V_{*} = \mu_{10} /\rho_{1} R_{2}$ and characterizes the relation between convective and diffusion forces; Darcy number $Da$, relation of elastic and viscous forces $K_{bez}$ and diffusion coefficients $\overline{D}$ together with $Pe_{D}$ determine the nature of the flow. parameters $\overline{\Omega }$, $\bar{\rho }$, α₁, α₂, β are not so significant.

To assess the dimensionless parameters, the following physical values were used that characterize the diffusing fluid (blood) and physical parameters of the capillary [27,28,29,30,31]: $\mu_{10} = 4.5 \times 10^{ - 3}$ Pa s, $\rho_{1} = 1064$ kg/m⁻³, $K = 2.2 \times 10^{9}$ Pa, $\alpha = 0.3$, $R_{1} = 3 \times 10^{ - 6}$ m, $R_{2} = 4 \times 10^{ - 6}$ m, $D_{1} = 2.1 \times 10^{ - 10}$ m²/s, $k_{f} = 0.5 \times 10^{ - 12}$ m². By using data above we can assess the region of alteration of dimensionless complexes: $0.38 \le Pe_{D} \le 1.43 \times 10^{3}$, $K_{bez} = 5.54 \times 10^{4}$. In the calculations, the following dimensionless parameters were varied: $m$, $Pe_{D}$, $\overline{D}$, $Da$ and $p_{10}$, $p_{20}$. The rest of the parameter were fixed: $C_{10}$ = 0.1, $C_{20}$ = 0, $\xi_{1}$ = 0.75, $\xi_{2}$ = 1, $\bar{\rho }$ = 1, $\alpha_{1}$ = 0.1, $\alpha_{2}$ = 0.1, $\beta$ = 1, $\overline{\Omega } = 0$.

The stationary problem for the porous wall (31)–(39) was solved numerically. In differential Eqs. (31), (32) and (34), the convective summand is approximated by the difference against the flow [32]. Such difference provides approximation of the convective summand for any direction of the flow velocity and yields stable algorithm. The initial distribution of velocities and concentrations is specified first. Then the differential equations for concentration and velocity are solved by the double-sweep method. Obtained distributions are used as initial for next iteration. The interface between media is distinguished explicitly. In the direct marching, the coefficients are found with a special approximation of boundary conditions in point at the interface. During reverse marching, we first find $C_{2}$ at the interface and then, by using first condition (37) in the point in interface, we find $C_{1}$. The same operations are applied to velocities. The process is repeated until a special condition is met. The calculation is carried out until a special condition is fulfilled—until a solution with a given accuracy is obtained. The variation of spatial steps changes the results no more than 1–5% in the wide region of varying model parameters.

6 Analysis of Results

The Peclet number which characterizes two flow regimes-convective ($Pe_{D} > 1$) and diffisive one ($Pe_{D} < 1$)—presents the main interest in the study of fluid transfer through a capillary with porous wall.

At small Peclet numbers, the main contribution to the distribution of concentrations in a capillary is made by diffusion. Since diffusion is a slow process, a smaller amount of a diffusant gets into the porous capillary wall (line 3 in Fig. 5a). With growing Peclet number ($Pe_{D}$ > 1), the contribution of convective diffusion becomes dominating; the flow velocity is higher in both areas (lines 1 in Fig. 5b). This leads to increased amount of the diffusant permeating the porous wall of the capillary (lines 1 and 2 in Fig. 5a). Line 2 in Fig. 5 corresponds to the transition regime, a convective-diffusive mass transfer. The main changes to concentration and velocity are observed in the vicinity of the interface $\xi = \Delta$.

Fig. 5

Distribution of concentration (a) and velocity (b) along the radius at different Peclet numbers 1—Pe = 10³, 2—Pe = 1, 3—Pe = 10⁻², $\overline{D}$ = 1, $m$ = 0.3, $Da$ = 0.01, $p_{10}$ = 2, $p_{20}$ = 0.2, $K_{bez} = 5.54 \times 10^{ - 2}$, $\Delta = 0.25$, $\overline{\Omega } = 0$

The redistribution of the diffusant concentration between the materials is appreciably affected by parameter $\overline{D}$ (relation of the diffusion coefficient in area 2 to the diffusion coefficient in area 1). At $\overline{D}$ > 1 the fraction of the diffusant in the capillary wall increases (Fig. 6a), while at $\overline{D}$ < 1 the diffusant is almost absent in area 2. It has almost zero effect on the velocity distribution (Fig. 6b). The character of concentration distribution both at convective (Fig. 6) and diffusive mass transfer is qualitatively similar under variation of $\overline{D}$. The difference is only in the velocity values.

Fig. 6

Distribution of concentration (a) and velocity (b) along the radius under convective mass transfer at different values of parameter $\overline{D}$, 1—$\overline{D}$ = 0.1, 2—$\overline{D}$ = 1, 3—$\overline{D}$ = 10, $Pe_{D}$ = 10³, $m$ = 0.3, $Da$ = 0.01, $p_{10}$ = 2, $p_{20} = 0.2$, $K_{bez} = 5.54 \times 10^{ - 2}$, $\Delta = 0.25$, $\overline{\Omega } = 0$

Increased capillary wall thickness decreases the concentration and velocity at the interface in both phases both under convective and diffusive mass transfer. This was demonstrated in Table 1, because it was difficult to demonstrate in a figure.

Table 1 Concentration and velocity at interface for different capillary wall thickness under convective mass transfer

Increased wall porosity decreases the concentration of the diffusant in the second area near the interface; however, the diffusant permeates deeper into the capillary wall under both convective (Fig. 7a, c) and diffusive (Fig. 7b, d) regimes. This is explained by increased volume of porous space and the diffusant moves more freely in the second area. The variation of porosity hardly affects the concentration distribution in the first area at any Peclet number. The concentration negligibly reduces only near the interface. The velocity behaves ambiguously (Fig. 7c, d) which is due to the interdependence of contrary physical mechanisms.

Fig. 7

Distribution of concentration (a, b) and velocity (c, d) along radius under convective (a, c) and diffusive (b, d) mass transfer and different values of parameter $m$, 1—$m$ = 0.15, 2—$m$ = 0.2, 3—$m$ = 0.25, 4—$m$ = 0.3, 5—$m$ = 0.35, $\overline{D}$ = 1, $Da$ = 0.01, $p_{10}$ = 2, $p_{20}$ = 0.2, $K_{bez} = 5.54 \times 10^{ - 2}$, $\Delta = 0.25$; $\overline{\Omega } = 0$

Decreased permeability (decreased Darcy number) negligibly reduces the concentration and reduces the velocity in both regions at any Peclet number.

The major impact on the velocity distribution is caused by the pressure gradient. An increase in the initial pressure in the first area (not shown) augments the velocity in both areas, while it has almost no effect on the concentration distribution; the concentration drops in both areas only in the interface vicinity. Similar behavior is observed under the diffusive regime of mass transfer. An increase in the initial pressure in the second area has no effect on the concentration distribution, while the velocity in both areas negligibly reduces in any regime.

All previous calculations were made with due regard to the concentration expansion. Parameter $\alpha$ which is included into dimensionless complex $K_{bez} = K\alpha R_{2}^{2} \rho_{1} /\mu_{10}^{2}$. This excites interest in the comparison of the concentration distribution and velocities in the porous wall with and without due consideration of this effect (Fig. 8). Evidently, without consideration of the concentration expansion, the velocity in the interface vicinity increases, which is valid for both sides of the interface. The concentration expansion causes more diffusant to permeate into the porous capillary wall. Such considerable difference is observed even at small values of coefficient $K_{bez}$.

Fig. 8

Distribution of concentration (a) and velocity (b) along the radius under convective mass transfer and for different values $K_{bez}$, 1—$K_{bez} = 5.54 \times 10^{ - 2}$, 2—$K_{bez} = 0$, $Pe_{D}$ = 10³, $\overline{D}$ = 1, $m$ = 0.3, $Da$ = 0.01, $p_{10}$ = 2, $p_{20}$ = 0.2, $\Delta = 0.25$; $\overline{\Omega } = 0$

The effect of viscosity versus concentration on concentration and velocity distributions is illustrated in the Fig. 9. An increase in viscosity with concentration leads to an increase in the fraction of diffusant in the capillary wall in the convective flow regime (Fig. 9a, c), and in the diffusion mode to an insignificant decrease (Fig. 9b, d). In this case, the velocity increases in the convective mode, and decreases in the diffusion mode.

Fig. 9

Distribution of concentration (a, b) and velocity (c, d) along radius under convective (a, c) and diffusive (b, d) mass transfer and different values of viscosity of liquid; $\overline{D}$ = 1, $Da$ = 0.01, $p_{10}$ = 2, $p_{20}$ = 0.2, $K_{bez} = 5.54 \times 10^{ - 2}$, $m$ = 0.3, $\Delta = 0.25$; $\overline{\Omega } = 0$

For all figures above it was accepted $\overline{\Omega } = 0$.

The mass flow affects the nature of the concentration distribution in the diffusion mode (Fig. 10b, d red lines), but in the convective mode, no effect is detected (Fig. 10a, c red lines). A smaller amount of diffusant remains in the capillary wall (Fig. 10b) when mass flow is taken into account, the speed also decreases (Fig. 10c).

Fig. 10

Distribution of concentration (a, b) and velocity (c, d) along radius under convective (a, c) and diffusive (b, d) mass transfer and different values of parameter $\overline{\Omega }$, 1—$\overline{\Omega }$ = 0, 2—$\overline{\Omega }$ = 10, $\overline{D}$ = 1, Da = 0.01, $p_{10}$ = 2, $p_{20}$ = 0.2, $K_{bez} = 5.54 \cdot 10^{ - 2}$, m = 0.3, $\Delta = 0.25$

7 Conclusions

The work suggested a model of biological fluid transfer in a selected macropore with microporous walls with due account for concentration expansion phenomena appearing in stet equation. For two flow regimes—convective ($Pe_{D} > 1$) and diffusive ($Pe_{D} < 1$)—we have studied the concentration distribution in the capillary wall. It was shown that the largest impact on the redistribution of concentration between the capillary volume and its porous wall is made by Darcy number Da and correlation of diffusion coefficients. The concentration of the diffusant in the porous layer increases with growing parameter $\overline{D}$ or decreasing porosity or permeability under diffusive mass transfer. The velocity in the interface vicinity increases with rising pressure in the capillary volume or under decreasing porosity at any Peclet number. It was discovered that the concentration expansion appreciably affects the distribution of velocity and concentration. The ambiguous impact of model parameters on different flow regimes is connected with the interrelation between contrary physical mechanisms. Described model contains practically significant parameters allowing understanding how the concentration distribution changes with flow type variation.