1 Introduction

The motivating disease behind this study is influenza type A, a recurrent communicable viral disease, known for its ability to change due to point (most common) or shift mutations. These variants are responsible for seasonal flu epidemics and sometimes pandemics. In 2009, a pandemic H1N1-strain of influenza type A was identified in Mexico, spreading quickly around the world. Influenza has significant impact on the world since it is responsible, for example, for nearly 40 000 deaths in the USA alone each year. Recurrent influenza outbreaks place a significant social and economic burden to society, and naturally, the possibility of the emergence of pandemic strains has worried the world community since the devastating impact of the 1918 global influenza pandemic. Consequently, the search for strategies that mitigate the impact of seasonal influenza and strategies that may be also effective in reducing morbidity and mortality in the case of a pandemia has always been of interest to the public health communities. Given the variability and inability to quickly produce highly effective vaccines and given the timing and uncertainty in the appearance and generation of new strains, the use of strategies based on isolation and/or quarantine (I and Q) as a way of containing communicable diseases in general (and influenza in particular) has been used for many years. The appearance in 2002 of the severe acute respiratory syndrome (SARS) was partially contained by the use of I and Q and fast diagnosis (Chowell et al. 2003). Moreover, isolation precautions have been applied to prevent the transmission of the 2009 H1N1 influenza A pandemic.

The effectiveness of I and Q isolation and quarantine policies is in general advantageous albeit in some instances (e.g., rubella and chicken pox in China), their use may have negative consequences (Castillo-Chavez et al. 2003). Although in the context of this manuscript the terms I and Q are used in some sense interchangeable (cite paper with my son), in general they have different meanings in the epidemiological and/or bio-security literature. Isolation (I ) typically means that symptomatic infected are separated from others during the duration of an outbreak, while quarantine (Q ) is understood to mean the use or implementation of deliberate policies that limit the free and natural movement of people who are infected or who may have been exposed to infectious individuals.

In this work, quarantine means that somehow the ability of individuals to infect others has been diminished. Specifically, only infected (assumed infectious) individuals are quarantined and the effect of such a policy impacts the transmission process in two ways. First, it reduces the effectiveness of the contacts with susceptibles, and second, it reduces their frequency in the environments where transmission takes place.

The role of quarantine has also been examined in the context of pandemic flu for over a century. Quarantine and isolation measures were put in place during the 1918 flu pandemic in every part of the world, including the USA (Barry 2005), but it was the emergence of SARS in 2002, which caused worldwide panic despite its ”low” number of cases (8000), that brought the potential value of quarantine and/or isolation effectiveness to the forefront of public health policy.

Isolation has historically been used to control contagious diseases with some success (Castillo-Chavez et al. 2003; Gensini et al. 2004). There is plenty of evidence that when applied properly, isolation helps prevent the transmission of a contagious disease as effective contact rates may be reduced long enough by setting infectious individuals apart from the “rest” of the population (Ebola paper with Diego on the Lancet). In general, the situation is rather complex since often the epidemiological status of individuals is not visible; latently infected individuals are sometimes asymptomatic and yet still able to transmit the disease (Ebola paper with Diego on the Lancet). Further, in general isolation and quarantine at large scales will be done primarily on a voluntary basis and so their success may depend primarily on the public trust and understanding of the necessity of such restrictions.

Mathematical models have been used to study their impact on the dynamics of infectious diseases under isolation and quarantine (I and Q) in order to test the effectiveness of various scenarios (strategies) on the prevention or amelioration of the spread of highly contagious diseases (Brauer and Castillo-Chávez 2012; Chowell et al. 2016; Feng and Thieme 1995; Hethcote et al. 2002; Nuño 2005). The implementation of quarantine has been assumed to be perfect in the sense that quarantined individuals have been completely separated from the rest of the population, that is, all contacts between quarantined infected and susceptible individuals have been eliminated with some of these models capable of supporting sustained oscillatory outbreaks. In addition, extensions of the SIQR model that deliberately include a class A of asymptomatic individuals have also been studied by Castillo-Chavez et al. (2003) and Vivas-Barber et al. (2014).

The purpose of this paper is to introduce and analyze a model that incorporates a partially effective quarantine (or isolation) policy to test the mathematical robustness of prior mathematical results to variations in isolation and quarantine effectiveness. Here, the degree of effectiveness (i.e., reducing the movement of quarantined individuals) is implemented through the use of a single parameter \(\sigma \) with a perfect quarantine/isolation model corresponding to \(\sigma =1\), which corresponds to the likelihood that a susceptible meets an infectious individual (within a homogeneously mixing populations) going from I / N to \({I}/{(N-Q)}\). In general, it will go from I / N to \({I}/{(N-\sigma Q)}\) with \(\sigma \in [0,1]\). It has been shown for the case \(\sigma =1\) that classical quarantine models can generate oscillations (Feng 1994; Hethcote et al. 2002). However, we show that if one uses communicable disease parameters that oscillations are less likely when \(\sigma \) varies in [0, 1]. Further, it is shown that for influenza parameters, oscillatory behavior takes place only when \(\sigma \) is very close to 1 or when \(\sigma =1\); periodic solutions arise via a Hopf bifurcation as \(\sigma \) varies in [0, 1]. Results on persistence and global stability of the equilibria that generalize those in Feng (1994) are also presented in this paper.

The paper is organized as follows. In Sect. 2, the standard SIQR model, where quarantine is assumed to be perfect, is introduced. In Sect. 3, a model variant with imperfect quarantine is formulated and analyzed, where the basic reproduction number \(R_0\) and model’s equilibria have been found. In this last case, the model is shown to exhibit Hopf bifurcation. In Sect. 4, global stability analysis of the infection-free equilibrium for \(R_0 < 1\) is established and uniform persistence proven. The paper includes a discussion of the results in Sect. 5.

2 The Standard Model

In this section, we revisit the analysis of the SIQR model shown in Hethcote et al. (2002), where S, I, Q and R stand for the number of susceptible, infected, quarantine and recovered individuals, respectively, so that \(S + I + Q + R = N\). In this model, the population is assumed to have constant size and its individuals are assumed to mix at random, so that every individual has the same chance to make contact with others. Here, a policy of perfect quarantine is considered. Thus, the incidence rate is given by \(\beta S {I}/{(N-Q)}\) where \(\beta \) is the per-capita and per-infected effective contact rate, that is the number of effective contacts leading to a secondary case of infection. It is assumed further that the recovery and quarantine per-capita rates are constant as in Hethcote et al. (2002). Hence, the mathematical representation of the above-described model is

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \mu N-\beta S\frac{I}{N-Q}-\mu S, \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \beta S\frac{I}{N-Q}-(\theta +\gamma +\mu )I, \\ \frac{\mathrm{d}Q}{\mathrm{d}t}= & {} \theta I-(\alpha +\mu )Q, \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \gamma I+\alpha Q-\mu R, \end{aligned}$$

where \(\mu \) is the per-capita birth and death rate, \(\gamma \) is the per-capita recovery rate, \(\theta \) is the per-capita isolation/quarantine rate, and \(\alpha \) is the per-capita recovery rate for isolated/quarantined individuals. State variables and parameters are defined in Tables 1 and 2. A thorough mathematical analysis of the above model, when \(\gamma =0\), is shown in Feng (1994) and Feng and Thieme (1995). Specifically, it is shown in Feng (1994), Feng and Thieme (1995) that the introduction of a fully isolated class could destabilize the endemic equilibrium in a susceptible-infected-quarantined-recovered (SIQR) model. Hethcote and his collaborators Hethcote et al. (2002) expanded the SIQR model via some variants that allowed for the movement of individuals to the Q-class at different stages and corroborated the results in Feng (1994), Feng and Thieme (1995). Nuño (2005) analyzed the impact of isolation/quarantine but in the context of a population that is facing two competing strains of influenza. She focused on the situation where the competition was mediated by cross-immunity. The introduction of a quarantine class into a two-strain model (mediated by cross-immunity) not only continues to prove its capability of generating sustained oscillations but also its ability to generate them within a range of acceptable for “flu” parameter values [not the situation in Feng (1994) and Feng and Thieme (1995)]. Furthermore, the oscillation periods seemed to be consistent with those associated with recurrent influenza outbreaks.

Isolation/quarantine is a complicated process because we do not live in a perfect world. In hospitals, patients may inadvertently or deliberately break from isolation and (in the process) have casual contacts with others including medical personnel, staff and visitors. In this work, we introduce and analyze a model that incorporates isolation, under the assumption that only a fraction of individuals in the Q compartment manages to stay totally isolated from the rest of the population.

3 Model with \(\sigma \)-Quarantine Class

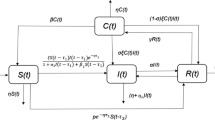
In the \(\sigma \)-quarantine model, it is assumed that the latency period is negligible and that immunity is permanent. Hence, using the same notation as above and following the flow diagram shown in Fig. 1, we come up with the \(\sigma \)-quarantine model

Table 1 Description of the model state variables
Full size table
Table 2 Description of the model parameters
Full size table
Fig. 1
figure 1

(Color figure online) Flowchart for the transition between model states

Full size image
$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \mu N-\beta S\frac{I}{N-\sigma Q}-\hat{\beta } S\frac{(1-\sigma ) Q}{N-\sigma Q}-\mu S, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \beta S\frac{I}{N-\sigma Q}+\hat{\beta } S\frac{ (1-\sigma ) Q}{N-\sigma Q}-(\theta +\gamma +\mu )I, \nonumber \\ \frac{\mathrm{d}Q}{\mathrm{d}t}= & {} \theta I-(\alpha +\mu )Q, \nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \gamma I+\alpha Q-\mu R \end{aligned}$$
(1)

where the state variables and parameters are defined in Tables 1 and 2, with \(\sigma \in [0,1]\). The parameter \(\sigma \) denotes the effectiveness of isolation/quarantine, where a value of \(\sigma = 0\) means that isolation/quarantine is totally ineffective, while \(\sigma = 1\) is equivalent to a totally perfect state of isolation/quarantine. The rate \(\lambda \) shown in the flowchart represents the force of infection (the rate at which susceptible individuals acquire the infection) and is such that

$$\begin{aligned} \lambda = \beta \frac{I}{N-\sigma Q} + \hat{\beta } \frac{(1-\sigma ) Q}{N-\sigma Q}. \end{aligned}$$

Specifically, as shown in Table 2, \(\beta \) represents the effective rate of contacts between susceptible and infected individuals, while \(\hat{\beta }\) represents the effective rate of contacts between susceptible and imperfectly quarantined individuals. Since \(\sigma \) represents the effectiveness of quarantine, then the total number of successfully quarantined individuals is \(\sigma Q\) and therefore the total number of individuals who are available to mix homogeneously is \((N-\sigma Q)\). Thus, if we have a susceptible individual, then the probability that this individual has a contact with an infected individual is \(I/(N-\sigma Q)\), while the probability that this susceptible individual encounters an imperfectly quarantined one is \((1-\sigma ) Q/(N - \sigma Q)\). Hence, the new incidences due to contacts with infected individuals are \(\beta S I/(N - \sigma Q)\), while those occurring due to contacts of susceptible with imperfectly quarantined individuals are \(\hat{\beta }(1-\sigma )S Q/(N-\sigma Q)\).

It is assumed that Q-individuals tend to avoid any kind of contacts that are most likely to lead to the transmission of the infectious agent. Hence, it is assumed that the average number of effective contacts per unit time involving quarantined individuals, \(\hat{\beta }\) is smaller than \(\beta \). Mathematically, we set \(\hat{\beta }\equiv r \beta \), where \( r \in [0,1]\). Therefore, if \( r =0\), then Q-individuals (while still in circulation) manage to avoid all risky contacts. On the other hand, if \( r =1\) then Q-individuals that circulate take no precautions to avoid passing the infection.

3.1 Rescaled and Reduced Model

If we put \( \bar{S} = S/N, \bar{I} = I/N, \bar{Q} = Q/N\) and \( \bar{R} = R/N\), then the model is rewritten in terms of proportions as

$$\begin{aligned} \frac{\mathrm{d} {\bar{S}}}{\mathrm{d}t}= & {} \mu -\beta {\bar{S}}\frac{[ {\bar{I}}+ r (1-\sigma ) {\bar{Q}}]}{1-\sigma {\bar{Q}}}-\mu {\bar{S}},\nonumber \\ \frac{\mathrm{d} {\bar{I}}}{\mathrm{d}t}= & {} \beta {\bar{S}}\frac{[ {\bar{I}}+ r (1-\sigma ) {\bar{Q}}]}{1-\sigma {\bar{Q}}}-(\theta +\gamma +\mu ) {\bar{I}}, \nonumber \\ \frac{\mathrm{d} {\bar{Q}}}{\mathrm{d}t}= & {} \theta {\bar{I}}-(\alpha +\mu ) {\bar{Q}},\nonumber \\ \frac{\mathrm{d} {\bar{R}}}{\mathrm{d}t}= & {} \gamma {\bar{I}}+\alpha {\bar{Q}}-\mu {\bar{R}} \end{aligned}$$
(2)

with initial conditions

$$\begin{aligned} \bar{S}(0)=1-\bar{I}_{0}, \quad \bar{I}(0)=\bar{I}_{0},\quad \bar{Q}(0)=0,\quad \bar{R}(0)=0. \end{aligned}$$

Thus, the variables \(\bar{S}, \bar{I}, \bar{Q}\) and \(\bar{R}\) denote the proportions of susceptible, infected, isolated/quarantined and recovered individuals, respectively; i.e., \(\bar{S} + \bar{I} + \bar{Q} + \bar{R} = 1\).

3.2 Equilibrium Analysis and the Basic Reproduction Number

3.2.1 IFE and \(R_0\)

On putting the derivatives in the left-hand side of system (2) equal zero and solving the resulting nonlinear algebraic system in terms of the variables \(\bar{S}, \bar{I}, \bar{Q}\) and \(\bar{R}\), we get that the model has an infection-free equilibrium (IFE) \(E_0=(1, 0, 0, 0)^{\prime }\) and a unique disease-endemic equilibrium \(E^* = (S^*, I^*, Q^*, R^*)\) that will be determined later on.

To investigate the local stability of \(E_0\), we linearize model (2) around \(E_0\) to get the corresponding Jacobian matrix. This matrix has two equal eigenvalues of negative value \(-\mu \), in addition to the eigenvalues of the submatrix

$$\begin{aligned} J_{0} = \left( \begin{array}{cc} \beta -(\theta +\gamma +\mu )&{} (1-\sigma ) r {\beta }\\ \theta &{}-(\alpha +\mu ) . \\ \end{array}\right) \end{aligned}$$

To guarantee the local asymptotic stability of the disease-free equilibrium \(E_0\), the conditions \(\mathrm{trace}(J_{0})< 0\) and \(\mathrm{det}(J_{0})>0\) should be held. Since

$$\begin{aligned} \mathrm{trace}(J_{0})=\beta -(\alpha +\mu )-(\theta +\gamma +\mu ) \end{aligned}$$

and

$$\begin{aligned} \mathrm{det}(J_{0})=(\alpha +\mu )(\gamma +\mu +\theta )-\beta (\alpha +\mu )-(1-\sigma ) r \beta \theta , \end{aligned}$$

then the condition \(\mathrm{det}(J_{0})>0\) implies the condition \(\mathrm{trace}(J_{0})< 0\). Hence, \(E_0\) is locally asymptotically stable if and only if \(R_0 < 1\) where

$$\begin{aligned} R_{0}= & {} \frac{\beta }{(\gamma +\mu +\theta )}+\frac{(1-\sigma ) r \beta \theta }{(\alpha +\mu )(\gamma +\mu +\theta )}\end{aligned}$$
(3)
$$\begin{aligned}= & {} \frac{\beta }{\gamma + \mu + \theta } \left[ 1 + (1-\sigma )\frac{ r \theta }{\alpha + \mu }\right] \end{aligned}$$
(4)

is the basic reproduction number.

The form (3) means that \(R_0\) is the additive contribution of the two infective classes (\(\bar{I}\) and \(\bar{Q}\)) to the generation of the secondary cases of infectious when \(\bar{S}(0)\approx 1\). Clearly, if \(r=0\), (totally effective quarantine), then \(R_0\) is reduced to what one gets when the Q-class is incapable of generating secondary cases of infections. On the other hand, if \(r = 1\) and \(\sigma = 0\), then we have the worst case scenario; that is, quarantine plays no role.

On the other hand, the form (4) shows clearly that \(R_0\) is the multiplication of two terms. The first term

$$\begin{aligned} \frac{\beta }{\gamma + \mu + \theta } \end{aligned}$$

represents the basic reproduction number for the model if the quarantine is totally perfect. However, the second term contains in part the expression

$$\begin{aligned} (1-\sigma )\frac{ r \theta }{\alpha + \mu } \end{aligned}$$

which represents the percent increase in the reproduction number due to the ineffectiveness of quarantine. We have therefore established the following stability result.

Theorem 1

System (2) has a unique disease-free equilibrium point \(E_{0}=(1,0,0,0)^{\prime }\), which is locally asymptotically stable for \(R_{0}\le 1\) and is unstable for \(R_{0}> 1\).

3.2.2 Existence and Stability of a Unique Endemic Equilibrium

The equilibrium analysis of the nonlinear dynamical system (2) shows that it has (in addition to the IFE) a unique endemic equilibrium corresponding to the persistence of the infection, for values of \(R_0 > 1\). The following theorem gives insight on that equilibrium and its local stability.

Theorem 2

If \(R_{0}> 1\), then system (2) has a uniquely determined nonnegative equilibrium point given by \(E^{*}=(S^{*},I^{*},Q^{*},R^{*})^{\prime }\), where \(S^{*}\), \(I^{*}\), \(Q^{*}\) and \(R^{*}\) are given by the following formulae ( in terms of \(R_{0}\))

$$\begin{aligned} I^{*}= & {} \frac{R_{0}-1}{bR_{0}-\sigma a}, \qquad Q^{*}=aI^{*}=a\frac{R_{0}-1}{bR_{0}-\sigma a}, \qquad S^{*}=1-bI^{*}=\frac{b-\sigma a}{bR_{0}-\sigma a}, \nonumber \\ R^{*}= & {} 1 - S^{*} - I^{*} - R^{*} = (b-a-1) \frac{R_{0}-1}{bR_{0}-\sigma a}= \frac{\gamma +\alpha a}{\mu } \times \frac{R_{0}-1}{bR_{0}-\sigma a} \end{aligned}$$
(5)

where

$$\begin{aligned} a=\frac{\theta }{\alpha +\mu } \quad \mathrm{and} \quad b=\frac{\gamma +\mu +\theta }{\mu }. \end{aligned}$$

In fact, it will be shown in Sect. 3.3 that a Hopf bifurcation may occur as parameters are varied. We see that the stability of \(E^{*}\) is characterized sometimes a stable spiral. We will see that periodic solutions around \(E^{*}\) can in fact be supported.

Proof

It is easy to check that the components of the disease-endemic equilibrium \(E^{*}\) of system (2) are given by (5). To investigate its stability, we compute its corresponding \(4\times 4\) Jacobian matrix. It could easily be checked that it has an eigenvalue \(-\mu (< 0)\), while the other three eigenvalues are those of the submatrix

$$\begin{aligned} J_\mathrm{sub}= & {} \left( \begin{array}{ccc} -A_1-\mu &{}\quad -B_1&{}\quad -C_1\\ A_1&{}\quad B_1-D_1&{}\quad C_1\\ 0&{}\quad \theta &{}\quad -E_1 \end{array}\right) \end{aligned}$$

with

$$\begin{aligned} A_1= & {} \beta \frac{I^{*}+ r (1-\sigma ) aI^{*}}{1-\sigma aI^{*}} = \beta \left( 1 - \frac{1}{R_0}\right) \left( \frac{1+(1-\sigma )r a}{b - \sigma a} \right) ,\\ B_1= & {} \beta \frac{1-bI^{*}}{1-\sigma aI^{*}} = \frac{\beta }{R_0} = \frac{(\alpha + \mu )(\gamma +\theta + \mu )}{\alpha + \mu + (1-\sigma )r \theta },\\ C_1= & {} \frac{r(1-\sigma ) + \sigma I^{*}}{1 - \sigma a I^{*}} B_1 = \frac{B_1}{b-\sigma a} \left( \sigma + (1-\sigma )rb - \frac{(1 + (1-\sigma )ra)\sigma }{R_0} \right) , \\ D_1= & {} \theta +\gamma +\mu \qquad \qquad \text {and}\quad E_1=\alpha +\mu . \end{aligned}$$

\(\square \)

The characteristic equation of \(J_\mathrm{sub}\) is a third-degree polynomial given by

$$\begin{aligned} P(\lambda )=a_{3}\lambda ^{3}+a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}, \end{aligned}$$
(6)

with coefficients

$$\begin{aligned} a_{3}= & {} 1,\\ a_{2}= & {} \mu + A_1+ E_1 +(D_1 - B_1),\\ a_{1}= & {} (\mu + A_1) E_1 + (\mu + E_1) (D_1 - B_1) + D_1 A_1 - \theta C_1,\\ a_{0}= & {} \mu E_1 (D_1 - B_1) + A_1 D_1 E_1 - \mu \theta C_1 . \end{aligned}$$

It is easy to check that

$$\begin{aligned} D_1 - B_1 = (\gamma + \theta + \mu ) \left( 1 - \frac{\alpha + \mu }{\alpha + \mu + (1-\sigma ) r \theta }\right) > 0. \end{aligned}$$

Hence, \(a_2 > 0\). Moreover, the coefficient \(a_1\) could be proven positive by considering it as a function of \(R_0\). To this end, we compute

$$\begin{aligned} a_1\vert _{R_0 = 1}= & {} \mu (\alpha + \mu ) + \mu (\gamma +\theta +\mu )\left( 1 - \frac{\alpha + \mu }{\alpha + \mu + (1-\sigma ) r \theta }\right)> 0,\\ \frac{\partial a_1}{\partial R_0}= & {} \frac{(\alpha +\mu )(\gamma +\theta + \mu )(1 + (1-\sigma )r a)}{(\alpha + \mu + (1-\sigma )r \theta )(b-\sigma a)} \left( \alpha {+} \gamma {+} 2\mu {+} \theta \left( 1 {-} \frac{\sigma }{R_0^2}\right) \right) {>} 0. \end{aligned}$$

Thus, \(a_1 > 0\). Similarly, we have

$$\begin{aligned} a_0\vert _{R_0 = 1}= & {} 0,\\ \frac{\partial a_0}{\partial R_0}= & {} \frac{(\alpha +\mu )(\gamma +\theta + \mu )(1 + (1-\sigma )r a)}{(\alpha + \mu + (1-\sigma )r \theta )(b-\sigma a)} \left( (\alpha {+} \mu )(\gamma {+} \mu {+} \theta ) {-} \frac{\sigma \mu \theta }{R_0^2}\right) {>} 0. \end{aligned}$$

Hence, \(a_0 > 0\) for \(R_0 > 1\). Thus, for \(R_0 > 1\), all coefficients of the characteristic polynomial (6) are positive.

Based on the application of the Routh–Hurwitz criteria, it remains to show that the Hurwitz determinants \(\Delta _{i}\) are all positive Lancaster (1969). For the third-degree polynomial (6), the Hurwitz determinants are given explicitly by \(\Delta _{1}=a_{2}\), \(\Delta _{2}=a_{2}a_{1}-a_{3}a_{0}\), and \(\Delta _{3} = a_{0} \Delta _{2}\) where

$$\begin{aligned} \Delta _{1}= & {} A_1+\mu +D_1+E_1-B_1 > 0,\\ \Delta _{2}= & {} (A_1+\mu +D_1+E_1-B_1)(A_1 D_1+D_1 E_1 +A_1 E_1\\&+\,\mu (D_1{+}E_1-B_1){-}B_1 E_1{-}\theta C_1){-}(A_1 D_1 E_1{+}\mu (D_1 E_1{-}B_1 E_1{-}\theta C_1)),\\ \Delta _{3}= & {} (A_1 D_1 E_1+\mu (D_1 E_1-B_1 E_1-\theta C_1))\Delta _{2}. \end{aligned}$$

The Hurwitz necessary and sufficient conditions for the local asymptotic stability require that all coefficients \(a_i\) as well as the determinants \(\Delta _i\) (\(i=1,2,3\)) should be positive. Now, since \(a_0> 0, \Delta _1 > 0\) and \(\Delta _3 = a_0 \Delta _2\), then the Hurwitz conditions are reduced to the inequality \(\Delta _2 > 0\). However, \(\Delta _2\) has subtracted terms so that it may have negative values for some range of the model parameters, which means that the Hurwitz conditions may not always be satisfied. Hence, for certain values of the parameters, some eigenvalues may cross the horizontal line to have purely imaginary values. Thus, a Hopf bifurcation may exist.

3.3 Existence of Hopf Bifurcation

Hopf bifurcation is the local appearance or disappearance of a periodic solution from an equilibrium when a parameter crosses a critical value. More precisely, it occurs when a branch of periodic solutions bifurcates from an equilibrium when that equilibrium loses its stability, as a complex conjugate pair of eigenvalues crosses the imaginary axis and changes its sign due to a change in the value of some model parameters (Guckenheimer and Holmes 1983). In terms of mathematical notations, in “Appendix B,” we state (without proof) the classical result of Hopf on the conditions exhibiting Hopf bifurcation and a lemma that gives equivalent conditions required for the existence of Hopf bifurcation.

In this work, we will numerically show that our model exhibits Hopf bifurcation by applying Lemma 5. Accordingly, since our characteristic polynomial (6) is of degree three and since all the coefficients \(a_{i}\) are positive and \(\Delta _{1}>0\), we will focus on the surface in parameter space where \(\Delta _2\) is zero. That is the surface where complex conjugate pair of eigenvalues is pure imaginary. The left subfigure of Fig. (2) shows the surface in the space \((\sigma , R_0, \theta )\) for fixed values of \(r, \mu , \alpha \) and \(\gamma \). It shows that there is a small “bump” for values of \(0.995< \sigma < 1\). A cross section for the Hopf surface in the space \((\alpha , R_0, \theta )\) is shown in the right subfigure of Fig. (2). The bump appearing in Fig. (2) (left) occurs at a value of \(R_0\) corresponding to the minimum value of \(\sigma \) at which Hopf bifurcation occurs. The value of \(\sigma \) at which Hopf bifurcation occurs is drawn as a function of \(R_0\), for different values of \(\theta \), in Fig. 3b. The figure shows that on the Hopf bifurcation surface, if we keep \(\theta \) fixed, then for a feasible value of \(R_0\), Hopf bifurcation starts to appear when \(\sigma = 1\). If we let \(R_0\) increases, then \(\sigma \) decreases till reaching a minimum after which it starts to increase again till reaching one. On the other hand, if we keep \(R_0\) fixed at a feasible level, but let \(\theta \) increases, then the value of \(\sigma \) that produces Hopf bifurcation decreases. Our results have also been realized using MATCONT. Figure 3a shows that the model exhibits Hopf bifurcation for parameter values as shown in the figure’s caption. It shows that the Hopf bifurcation occurs for very high enough values of \(\sigma \) (very close to 1). Time series analysis and phase space solutions are shown in Figs. (4, 5). For \(\sigma = 1\) and other parameter values as in the captions, the analysis shows the existence of limit cycles, see Fig. (4). However, if \(\sigma \) is reduced enough, while other parameter values are kept fixed as in Fig. (4), then the analysis shows that the trajectories are inward spirals, see Fig. (5).

Fig. 2
figure 2

(Color figure online) Hopf bifurcation surface in the space (\(\sigma , R_0, \theta \)) for parameter values \(\mu = 1/3650\approx 0.00027397, \gamma = 0.5, \alpha = 0.4\) per week and \(r=0.11\) (left figure). The right figure shows the cross section of the Hopf surface in the \((\alpha , R_0, \theta )\) space for parameter values \(\mu = 1/3650, \gamma = 0.5\) per week, \(r=0.11\) and \(\sigma = 1\)

Full size image
Fig. 3
figure 3

(Color figure online) a Curve obtained using MATCONT that represents the values of \(\sigma \) and the real part of one of the complex eigenvalues. The mark represents the point at which the Hopf bifurcation appears at \(\sigma =0.9973971\). Simulations are done with parameter values \(\mu = 1/3650, \gamma = 0.5, \alpha \,=\,0.4, \theta \,=\,4\) per week, \(r\,=\,0.11\) and \(R_0\,=\,2.5\). b The critical value of \(\sigma \) at which Hopf bifurcation appears as a function of \(R_0\) for different values of \(\theta \), while the other parameters are kept fixed as in part (a)

Full size image
Fig. 4
figure 4

(Color figure online) For the values of the parameters \(\mu = 1/3650, \alpha =0.4, \gamma =0.5, \theta = 4\) per week, \(r = 0.11, R_0=2.5\) and \(\sigma =1\) we can see that trajectories of the infectives oscillate. The orbits in the phase space suggest the existence of limit cycles

Full size image
Fig. 5
figure 5

(Color figure online) For the values of the parameters \(\mu = 1/3650, \alpha =0.4, \gamma =0.5, \theta = 4\) per week, \(r = 0.11, R_0=2.5\) but \(\sigma = 0.8\), we can see that trajectories of the infectives are damped. The orbits in the phase space are inward spirals

Full size image

4 Global Stability and Uniform Persistence

Model (2) could be rescaled by putting

$$\begin{aligned} x=\frac{\bar{S}}{A},\qquad y=\frac{\bar{I}}{A},\qquad q=\frac{(1-\sigma ) \bar{Q}}{A},\qquad z=\frac{\bar{R}}{A} \end{aligned}$$

where

$$\begin{aligned} A = 1-\sigma \bar{Q} \quad \text {and}\quad \frac{\mathrm{d}A}{\mathrm{d}t} = - \sigma \frac{\mathrm{d}\bar{Q}}{\mathrm{d}t}=-\sigma \theta \bar{I}+\sigma (\alpha +\mu )\bar{Q} \end{aligned}$$

and introduce the rescaled parameters

$$\begin{aligned} \hat{\alpha }=\frac{\alpha }{\beta },\qquad \hat{\theta }=\frac{\theta }{\beta },\qquad \hat{\gamma }=\frac{\gamma }{\beta },\qquad \hat{\mu }=\frac{\mu }{\beta } \end{aligned}$$

and rescaled time \( s = \beta t\) leading to the following equivalent system

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}= &{}\hat{\mu }(1-x) +\frac{\sigma }{1-\sigma } \hat{\mu }q - x y +x(\sigma \hat{\theta }y-(m+ r )q), \\ \dot{y}=&{} r xq+y(x+\sigma \hat{\theta }y-mq-(\hat{\theta }+\hat{\gamma }+\hat{\mu })), \\ \dot{q}=&{}(1+\frac{\sigma }{(1-\sigma )}q)(\hat{\theta }(1-\sigma ) y-(\hat{\alpha }+\hat{\mu })q), \\ \dot{z}=&{}\frac{1}{(1-\sigma )}\hat{\alpha }q-\hat{\mu }z+\hat{\gamma }y+z(\sigma \hat{\theta }y-m q), \\ \end{array} \right. \end{aligned}$$
(7)

where the dot means differentiation with respect to s (i.e., \( \dot{x}={dx}/{ds}\)) and \(m={\sigma (\alpha +\mu )}/{[(1-\sigma )\beta ]}\). The relation \(A=1-\sigma \bar{Q}\) implies that

$$\begin{aligned} x+y+q+z=1. \end{aligned}$$
(8)

The use of relation (8) means that one of the equations in (7) is “redundant.” The elimination of the equation for \(\dot{x}\) leads to the following three-dimensional equivalent system of nonlinear differential equations.

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{y}=&{} (r q + y)(1-y-q-z)+y(\sigma \hat{\theta }y-mq-(\hat{\theta }+\hat{\gamma }+\hat{\mu })), \\ \dot{q}=&{}(1+\frac{\sigma }{(1-\sigma )}q)(\hat{\theta }(1-\sigma ) y-(\hat{\alpha }+\hat{\mu })q), \\ \dot{z}=&{}\frac{1}{(1-\sigma )}\hat{\alpha }q-\hat{\mu }z+\hat{\gamma }y+z(\sigma \hat{\theta }y-m q), \\ \end{array} \right. \end{aligned}$$
(9)

As model (7) monitors human population, all its parameters and state variables should be nonnegative for \(t > 0\). Moreover, in order that this model makes epidemiologically meaningful sense, it is important to prove that all its state variables are nonnegative for all times. That is, we need to show that solutions starting with initial positive values remain positive for all time \(t > 0\). Therefore, we state and prove theorem [3] that determines the basic dynamical features of model (7). Its proof is deferred to “Appendix A.”

Theorem 3

Let \(x_{0}\), \(y_{0}\), \(q_{0}\), \(z_{0}\) \(\ge 0\) , \(x_{0}+y_{0}+q_{0}+z_{0}=1\). Then there exists a unique solution x, y, q and z of (7) with initial data \(x_{0}\), \(y_{0}\), \(q_{0}\), \(z_{0}\) at time 0 that is defined for all forward times. Moreover, x, y, q and z are nonnegative, where \(x+y+q+z=1\). If \(y_{0}=0\), then \(y(t)\equiv 0\). If \(y_{0}> 0\), then x(t), y(t), q(t), z(t) are strictly positive for all \(t> 0\). Furthermore, q is bounded by \(\hat{q}\), where \(\hat{q}=\max \{q_{0},(1-\sigma )\frac{\hat{\theta }}{\hat{\alpha }+\hat{\mu }}\}\).

4.1 Global Stability of the Infection-free Equilibrium

We start this section by introducing some notation that is needed in the analysis below. For a bounded real-valued function f on \([0,\infty )\), we define

$$\begin{aligned} f_{\infty }=\liminf _{t\rightarrow \infty }f(t),\quad f^{\infty }=\limsup _{t\rightarrow \infty }f(t). \end{aligned}$$

We also define

$$\begin{aligned} u:=\frac{y}{1+\frac{\sigma }{(1-\sigma )}q}. \end{aligned}$$
(10)

Thus, from (7) we get

$$\begin{aligned} \dot{u}=u\left[ x\left( 1+ r \frac{q}{y}\right) -(\hat{\theta }+\hat{\gamma }+\hat{\mu })\right] . \end{aligned}$$
(11)

Now, to establish the global asymptotic stability of the infection-free equilibrium, two lemmas are needed. The first lemma is known as the fluctuation lemma and it will be stated without proof, while the second lemma will be stated with a detailed proof.

Lemma 1

Let \(f:[0,\infty )\rightarrow \mathbf {R}\) be bounded and twice differentiable with bounded second derivative. Then there are sequences \(t_{n}\rightarrow \infty \), \(s_{n}\rightarrow \infty \) such that for all \(n \rightarrow \infty \), it holds \(\lim _{n\rightarrow \infty }f(t_{n})=f^{\infty }\), \(\lim _{n\rightarrow \infty }f(s_{n})=f_{\infty }\), \(f'(t_{n})=f'(s_{n})=0\), \(f''(t_{n}) \le 0\) and \(f''(s_{n}) \ge 0\) , \(n \in N\).

Lemma 2

If u converges, so do y, q and z.

Proof

In Theorem 3, we proved that the set

$$\begin{aligned} D=\{(x,y,q,z): 0\le x\le 1, 0\le y \le 1, 0\le q \le \kappa , 0\le z \le 1\} \end{aligned}$$

is forward invariant for any \(\kappa \ge {(1-\sigma )\hat{\theta }}/{(\hat{\alpha }+\hat{\mu })}\). A direct use of Lemma 1 means that we can choose two sequences \({t_n}\) and \({s_n}\) with \(t_{n}\rightarrow \infty \) and \(s_{n}\rightarrow \infty \) such that

$$\begin{aligned} q(t_{n})\rightarrow q^{\infty },\quad \dot{q}(t_{n})\rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} q(s_{n})\rightarrow q_{\infty },\quad \dot{q}(s_{n})\rightarrow 0. \end{aligned}$$

Then from (7) we have

$$\begin{aligned} q^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y^{\infty },\quad q_{\infty }\ge \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y_{\infty }. \end{aligned}$$
(12)

Using (11) and (12), we have

$$\begin{aligned} q^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}(1+\frac{\sigma }{(1-\sigma )}q^{\infty })u^{\infty }, \end{aligned}$$

and

$$\begin{aligned} q_{\infty }\ge \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y_{\infty }\ge \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}(1+\frac{\sigma }{(1-\sigma )}q_{\infty })u_{\infty }. \end{aligned}$$

Therefore, since u converges, then \(u^{\infty }=u_{\infty }\). Consequently,

$$\begin{aligned} \frac{q^{\infty }}{1+\frac{\sigma }{(1-\sigma )}q^{\infty }}\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}u^{\infty }=\frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}u_{\infty }\le \frac{q_{\infty }}{1+\frac{\sigma }{(1-\sigma )}q_{\infty }} \end{aligned}$$

and

$$\begin{aligned} q^{\infty }\left( 1+\frac{\sigma }{(1-\sigma )}q_{\infty }\right) \le q_{\infty }\left( 1+\frac{\sigma }{(1-\sigma )}q^{\infty }\right) . \end{aligned}$$

It follows that \(q^{\infty }\le q_{\infty }\) and therefore that q converges. From (10), it follows that y also converges.

To show that z converges, we let \(\bar{y}=y^{\infty }=y_{\infty }\), \( \bar{q}=q^{\infty }=q_{\infty }\). Applying Lemma 1 to the \(\dot{z}\) equation in (7) means that we can choose two sequences \({t_n}\) and \({s_n}\) with \(t_{n}\rightarrow \infty \) and \(s_{n}\rightarrow \infty \) such that

$$\begin{aligned} z(t_{n})\rightarrow z^{\infty },\quad \ddot{z}(t_{n}) \rightarrow 0,\quad z(s_{n})\rightarrow z_{\infty },\quad \ddot{z}(s_{n}) \rightarrow 0. \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{\hat{\alpha }}{(1-\sigma )}\bar{q}-\hat{\mu }z_{\infty }+\hat{\gamma }\bar{y}+\sigma \hat{\theta }\bar{y}z_{\infty }-m \bar{q}z_{\infty }\le & {} \frac{\hat{\alpha }}{(1-\sigma )}\bar{q}-\hat{\mu }z^{\infty }\nonumber \\&+\,\hat{\gamma }\bar{y}+\sigma \hat{\theta }\bar{y}z^{\infty }-m \bar{q}z^{\infty } \end{aligned}$$

or, equivalently,

$$\begin{aligned} \hat{\mu }z^{\infty }+(m \bar{q}-\sigma \hat{\theta }\bar{y})z^{\infty }\le \hat{\mu }z_{\infty }+(m \bar{q}-\sigma \hat{\theta }\bar{y})z_{\infty }. \end{aligned}$$

From (12) we have that \( m \bar{q}=\sigma \hat{\theta }\bar{y}\) and therefore \(z^{\infty }\le z_{\infty }\). That is, z converges. \(\square \)

Theorem 4

For model (7), if \(R_{0} < 1\), then the unique disease-free equilibrium point \(E_{0}=(1, 0, 0, 0)\) of system (7) is globally asymptotically stable.

Proof

Let \(R_{0}\le 1\). The use of Lemma 1 means that we can choose a sequence \({t_n}\) with \(t_{n}\rightarrow \infty \) such that

$$\begin{aligned} u(t_{n})\rightarrow u^{\infty },\quad \dot{u}(t_{n})\rightarrow 0. \end{aligned}$$

Direct use of (11) and (12) implies that

$$\begin{aligned} 0\le \left( 1+\frac{(1-\sigma )r\hat{\theta }}{\hat{\alpha }+\hat{\mu }}\right) u^{\infty }\left( x^{\infty }-\frac{1}{R_{0}}\right) \end{aligned}$$

Since \(\frac{1}{R_{0}}> 1\) and \(x^{\infty }\le 1\), we have \(u^{\infty }\le 0\). However, \(u\ge 0\), and therefore, \(u^{\infty }\ge 0\) from which it follows that \(u(t)\rightarrow 0\) as \(t\rightarrow \infty .\) In addition, since \(q^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }},\) then it follows from (10), (12) and the fact that \(u^{\infty }\ge 0\) that

$$\begin{aligned} y^{\infty }\le \left( {1+\frac{\sigma }{(1-\sigma )}q}\right) u^{\infty }=0,\quad q^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}\left( {1+\frac{\sigma }{(1-\sigma )}q}\right) u^{\infty }=0. \end{aligned}$$

Therefore, \(y(t)\rightarrow 0\), \( q(t)\rightarrow 0\) as \(t\rightarrow \infty .\) Using Lemma 1, the z equation in (7) and \(y^{\infty }=q^{\infty }=0\), we can show that \(z^{\infty }=0\). That is, we have that \(z(t)\rightarrow 0\) as \(t\rightarrow \infty \) and therefore

$$\begin{aligned} x(t)=1-y(t)-z(t)-q(t)\rightarrow 1\quad as\quad t\rightarrow \infty . \end{aligned}$$

Let \(R_{0}=1\). From (11) and the fact that \( \dot{u}(t)\le 0\), we conclude that u(t) converges. There are two cases.

  • Case 1, \(u(t)\rightarrow 0\) as \(t\rightarrow \infty .\) Similar to the proof for \(R_{0}<1\), it can be easily shown that

    $$\begin{aligned} y(t)\rightarrow 0,\quad q(t)\rightarrow 0, \quad z(t)\rightarrow 0\quad \mathrm{and} \quad x(t)\rightarrow 1\quad as\quad t\rightarrow \infty . \end{aligned}$$

  • Case 2, \(u^{\infty }>0.\) Choose \({t_n}\) with \(t_{n}\rightarrow \infty \) and such that \(u(t_{n})\rightarrow u^{\infty }\) and \(\dot{u}(t_{n})\rightarrow 0\). Then from (11) we see that \(u(t_{n})(x(t_{n})-1)\rightarrow 0\) as \(n\rightarrow \infty \). Since \(u^{\infty }>0\), we have \(x(t_{n})\rightarrow 0\) and therefore \(x_{\infty }\ge 1\). However, since it is also true that \(x^{\infty }\le 1\), \(x^{\infty }=x_{\infty }=1.\) Consequently,

    $$\begin{aligned} x(t)\rightarrow x^{\infty }=1\quad as \quad t\rightarrow \infty . \end{aligned}$$

    We conclude from (8) that \(y(t)\rightarrow y^{\infty }=0\), \(q(t)\rightarrow q^{\infty }=0\) and \(z(t)\rightarrow z^{\infty }=0\) as \(t\rightarrow \infty \).

\(\square \)

4.2 Uniform Persistence

In this subsection, we study the uniform persistence of our rescaled model (7). Before going into details, we state and prove two lemmas which are needed in the analysis later on.

Lemma 3

Let \(R_{0}>1\). If \(u(0)>0\), then u does not converge to 0 and \(x_{\infty }\le \frac{1}{R_{0}}.\)

Proof

Assume that \(u(t)\rightarrow 0\) as \(t\rightarrow \infty .\) Then the fluctuation lemma guarantees that there exists a sequence \({t_n}\) with \(t_{n}\rightarrow \infty \) such that \(u(t_{n})\rightarrow 0\) as \(n\rightarrow \infty \) and \(\dot{u}(t_{n})<0.\) From (12), we see that if u(t) goes to zero then y(t) and q(t) also go to zero. Then making the use of z equation in (7) and Lemmas 1 and 2, it is easily shown that z(t) goes to zero and therefore, \(x(t)\rightarrow 1\) as \(t\rightarrow 0\). Since \(R_{0}>1\), \(x(t_{n})-\frac{1}{R_{0}}>0\) for sufficiently large n. Hence, from (11) it is seen that \(\dot{u}(t_{n})\ge 0\) but since \(\dot{u}(t_{n})<0\), we have reached a contradiction. Therefore, u(t) does not go to zero.

Now, from (11), we have

$$\begin{aligned} \dot{u} = u\left[ x\left( 1+ r \frac{q}{y}\right) -\left( \theta +\gamma +\mu \right) \right] \ge u\left[ x\left( 1+ r \frac{q_{\infty }}{y}\right) -\left( \hat{\theta }+\hat{\gamma }+\hat{\mu }\right) \right] . \end{aligned}$$
(13)

Therefore, with the application of the fluctuation method, there exists a sequence \((t_n)\) such that \(t_n \rightarrow \infty , u(t_n) \rightarrow u_{\infty }\) and \(\dot{u}(t_n) \rightarrow 0\) as \(n \rightarrow \infty \). Hence,

$$\begin{aligned} 0 \ge u_{\infty } \left[ x_{\infty }\left( 1 + r q_{\infty }/y_{\infty }\right) - (\hat{\theta }+ \hat{\gamma }+\hat{\mu })\right] \end{aligned}$$

and with the help of (12) we have

$$\begin{aligned} x_{\infty } \le \frac{\hat{\theta }+ \hat{\gamma }+ \hat{\mu }}{1 + r q_{\infty }/y_{\infty }} \le \frac{\hat{\theta }+ \hat{\gamma }+ \hat{\mu }}{1 + r (1-\sigma )\hat{\theta }/(\hat{\alpha }+ \hat{\mu })} = 1/R_{0}. \end{aligned}$$

Thus, \(x_{\infty } \le \frac{1}{R_0}\) and the proof of Lemma 3 is now complete. \(\square \)

Lemma 4

Let \(R_{0}>1\) and \(y(0)>0\). Then there exists a small \(\delta >0\) independent of y(0) such that \(y^{\infty }>\delta .\)

Proof

By the z-equation in (7) we have

$$\begin{aligned} \dot{z}\le \frac{\alpha }{(1-\sigma )}q-\hat{\mu }z+\hat{\gamma }y+\sigma \hat{\theta }y. \end{aligned}$$

The fluctuation lemma guarantees the existence of a sequence \({t_n}\) with \(t_{n}\rightarrow \infty \) such that \(z(t_{n})\rightarrow z^{\infty }\) and \(\dot{z}(t_{n})\rightarrow 0\) as \(n\rightarrow \infty .\) Therefore,

$$\begin{aligned} 0\le \frac{\hat{\alpha }}{(1-\sigma )}q^{\infty } - \hat{\mu }z^{\infty } + \hat{\gamma }y^{\infty } + \sigma \hat{\theta }y^{\infty } \end{aligned}$$

and using (12) we have that

$$\begin{aligned} z^{\infty }\le & {} \frac{\hat{\alpha }}{(1-\sigma )\hat{\mu }}q^{\infty }+\frac{\hat{\gamma }+\sigma \hat{\theta }}{\hat{\mu }}y^{\infty }\\ z^{\infty }\le & {} \frac{\hat{\alpha }}{(1-\sigma )\hat{\mu }}\frac{(1-\sigma )\hat{\theta }}{(\hat{\alpha }+\hat{\mu })}y^{\infty }+\frac{\hat{\gamma }+\sigma \hat{\theta }}{\hat{\mu }}y^{\infty }\\ z^{\infty }\le & {} \left( \frac{\hat{\alpha }\hat{\theta }}{\hat{\mu }(\hat{\alpha }+\hat{\mu })}+\frac{\hat{\gamma }+\sigma \hat{\theta }}{\hat{\mu }}\right) y^{\infty }\\ y^{\infty }+z^{\infty }+q^{\infty }\le & {} \left( 1+\frac{\hat{\alpha }\hat{\theta }}{\hat{\mu }(\hat{\alpha }+\hat{\mu })}+\frac{\hat{\gamma }+\sigma \hat{\theta }}{\hat{\mu }}+\frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}\right) y^{\infty }. \end{aligned}$$

The use of Equation (8) leads to

$$\begin{aligned} y^{\infty }+z^{\infty }+q^{\infty }\ge (y+q+z)^{\infty }=(1-x)^{\infty }=1-x_{\infty } \end{aligned}$$

and by Lemma 3 we have that \(x_{\infty }\le \frac{1}{R_{0}}\); therefore,

$$\begin{aligned} y^{\infty }+z^{\infty }+q^{\infty }\ge 1-\frac{1}{R_{0}}>0 \end{aligned}$$

which implies that

$$\begin{aligned} y^{\infty }\ge \delta \end{aligned}$$

where \(\delta =(1+\frac{\hat{\alpha }\hat{\theta }}{\hat{\mu }(\hat{\alpha }+\hat{\mu })}+\frac{\hat{\gamma }+\sigma \hat{\theta }}{\hat{\mu }}+\frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }})^{-1}(1-\frac{1}{R_{0}}).\) \(\square \)

In addition to the above-mentioned lemmas, we need the following persistence results which are taken from (Thieme 1993). Let us consider the system \(\dot{y}=h(y)\) on \(\mathbf {R}^{n}\) and define a metric space (U, d), where U is the union of two disjoint subsets \(U_{1}\) and \(U_{2}\) of \(\mathbf {R}^{n}\). Assume that the solution of \(\dot{y}=h(y)\) exists for all \(t\ge 0\) if \(y(0)\in U_{1}\). Let \(U_{1}\) be an open set in U and \(y(t,y_0)\) be continuous solution in \(U_{1}\) with \(y(0)=y_0\), i.e., \(y(t,y_0)\in U_{1}\) for all \(t\ge 0\) and \(y_0\in U_{1}\). The distance between two points \(x=(x_1,x_2,\ldots ,x_n)\) and \(y=(y_1,y_2,\ldots ,y_n)\) is given by

$$\begin{aligned} d(x,y)=\sum _{k=1}^{n}\left| x_k-y_k\right| , \end{aligned}$$

and the distance of a point \(x\in U\) from a subset E of U is defined by

$$\begin{aligned} d(x,E)=\inf _{u\in E}d(x,u). \end{aligned}$$

Let us further give the following definitions and theorem as stated in Thieme (1993).

Definition 1

\(U_2\) is called a uniform weak repeller for \(U_1\) if

$$\begin{aligned} \limsup _{t\rightarrow \infty }d(y(t,y_0),U_2)>\epsilon , \end{aligned}$$

for all \(y_0\in U_1\), for some \(\epsilon >0\) that is independent of \(y_0\).

Definition 2

\(U_2\) is called a uniform strong repeller for \(U_1\) if

$$\begin{aligned} \liminf _{t\rightarrow \infty }d(y(t,y_0),U_2)>\epsilon , \end{aligned}$$

for all \(y_0\in U_1\), for some \(\epsilon >0\) that is independent of \(y_0\).

Theorem 5

Let (U, d) be locally compact metric space and let U be the disjoint union of two sets \(U_1\) and \(U_2\) such that \(U_2\) is compact. Let \(\Phi \) be a continuous semi-flow on \(U_1\). Then \(U_2\) is a uniform strong repeller for \(U_1\), whenever it is a uniform weak repeller for \(U_1\).

We now state and prove the following theorems on the uniform persistence of our system.

Theorem 6

For \(R_0 > 1\), model (9) is uniformly persistent. That is, the solutions are eventually uniformly bounded by positive constants from both below and above.

Proof

Let \(R_0>1\) and choose

$$\begin{aligned} U_1= & {} \{(y,q,z): 0< y \le 1, 0\le q \le \kappa , 0\le z \le 1\}\\ U_2= & {} \{(0,q,z): 0\le q \le \kappa , 0\le z \le 1\} \end{aligned}$$

where \(\kappa \ge {(1-\sigma )\hat{\theta }}/{(\hat{\alpha }+\hat{\mu })}\). \(U_1\) and \(U_2\) are two disjoint subset of \(\mathbf {R^{3}}\). It can be easily shown that for the given \(U_1\) and \(U_2\), \(U_2\) is compact and \(U=U_1UU_2\) is also compact. Note that \(y(t)>0\) if \(y(0)>0\) and therefore by Theorem 3, we have \((y(t),q(t),z(t))\in U_1\) if \((y(0),q(0),z(0))\in U_1\) and hence, \(q(0) < \kappa \) and \(q^{\infty }\le {(1-\sigma )\hat{\theta }}/{(\hat{\alpha }+\hat{\mu })}\); therefore, there exists a \(t_1>0\) such that

$$\begin{aligned} q(t_1)<\frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}+\frac{1}{2}\left( \kappa -\frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}\right) \le \kappa . \end{aligned}$$

Therefore, without lose of generality, it can be assumed that \((y(0),q(0),z(0))\in U_1\) for all solutions. By Lemma 4, \(y^{\infty }>\delta \) as long as \(y_0=y(0)>0\) where \(\delta \) is independent of the initial conditions. Hence, if \((y_0, q_0, z_0)\in U_1\) then

$$\begin{aligned} \limsup _{t\rightarrow \infty }d((y(t,y_0),q(t,q_0),z(t,z_0)),U_2)>\delta , \end{aligned}$$

that is, \(U_2\) is a uniform weak repeller for \(U_1\). From Theorem 5, it follows that \(U_2\) is a uniform strong repeller for \(U_1\). Hence, there is a \(\delta _1\) independent of the initial conditions such that

$$\begin{aligned} \liminf _{t\rightarrow \infty }d((y(t,y_0),q(t,q_0),z(t,z_0)),U_2)>\delta _1. \end{aligned}$$

Now, since \(d((y(t,y_0),q(t,q_0),z(t,z_0)),U_2) = y(t, y_0)\), then \(\liminf _{t\rightarrow \infty }y(t,y_0) > \delta _1\). Thus, \(y_{\infty }>\delta _1\). Further, since

$$\begin{aligned} \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y_{\infty }\le q_{\infty }\le q^{\infty }\le \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y^{\infty }, \end{aligned}$$

the use of the z-equation in (7) and Lemma 1 means that we can choose a sequence \({t_n}\) with \(t_n\rightarrow \infty \) such that \(z(t_n)\rightarrow z_{\infty }\) and \(\dot{z}(t_n)\rightarrow 0\). Therefore,

$$\begin{aligned} 0\ge & {} \frac{\hat{\alpha }}{(1-\sigma )}q_{\infty }-\hat{\mu }z_{\infty }+\hat{\gamma }y_{\infty }+\sigma \hat{\theta }y_{\infty }z_{\infty }-m q^{\infty }z_{\infty }\\\ge & {} \frac{\hat{\alpha }}{(1-\sigma )}q_{\infty }-\hat{\mu }z_{\infty }-m q^{\infty }z_{\infty }\\\ge & {} \frac{\hat{\alpha }}{(1-\sigma )}q_{\infty }-(\hat{\gamma }+\hat{\mu }+\hat{\theta }) z_{\infty } \end{aligned}$$

or equivalently

$$\begin{aligned} z_{\infty }\ge \frac{\hat{\alpha }}{(1-\sigma )(\hat{\gamma }+\hat{\mu }+\hat{\theta })}q_{\infty }. \end{aligned}$$

The fact that \(R_0>1\) and \(q_{\infty }\ge \frac{(1-\sigma )\hat{\theta }}{\hat{\alpha }+\hat{\mu }}y_{\infty }\) leads to

$$\begin{aligned} z_{\infty }\ge \frac{\hat{\alpha }}{(1-\sigma )(\hat{\gamma }+\hat{\mu }+\hat{\theta })}q_{\infty }\ge \frac{\hat{\alpha }\hat{\theta }}{\hat{\alpha }+\hat{\mu }+ r (1-\sigma )\hat{\theta }}y_{\infty }. \end{aligned}$$

Further,

$$\begin{aligned} x^{\infty }=1-y^{\infty }-q^{\infty }-z^{\infty }\le 1-y_{\infty }-q_{\infty }-z_{\infty }, \end{aligned}$$

completing the proof. \(\square \)

Theorem 7

Let \(R_0>1\) and \(y(0)>0\) and define

$$\begin{aligned} \bar{x}(t)=\frac{1}{t}\int _{0}^{t}x(s)\mathrm{d}s \end{aligned}$$

Then

$$\begin{aligned} \limsup _{t\rightarrow \infty }\bar{x}(t)\le \left( 1+\frac{ r (1-\sigma )\theta }{\alpha +\mu }\right) x^{*}. \end{aligned}$$

Proof

By Theorem 2, we know that there exists a unique positive equilibrium point \((S^{*},I^{*},Q^{*})\) for \(R_0>1\) of system (2). \(x^{*}=\frac{S^{*}}{A^{*}}=\frac{1}{R_0}\). We also know from Theorem 6 that y(0) is bounded away from zero and therefore I(0) is also bounded away from zero. Therefore, from the equation for \(I'(t)\) in System (2), we conclude that

$$\begin{aligned} I'(t)= & {} \beta S\frac{[I+ r (1-\sigma ) Q]}{A}-(\theta +\gamma +\mu )I,\\ I'(t)\ge & {} \beta S\frac{I}{A}-(\theta +\gamma +\mu )I,\\ \frac{I'(t)}{I(t)}\ge & {} \beta \frac{S}{A}-(\theta +\gamma +\mu ). \end{aligned}$$

Integrating both sides of the last inequality gives

$$\begin{aligned} \ln I(t)-\ln I(0)\ge \beta \int _{0}^{t}x(s)\mathrm{d}s-(\theta +\gamma +\mu )t. \end{aligned}$$

Dividing both sides by \(\beta t\) and taking the limit as t goes to infinity give

$$\begin{aligned} 0\ge \limsup _{t\rightarrow \infty }\bar{x(t)}-({\theta }+{\gamma } +{\mu }). \end{aligned}$$

Dropping the hats and making the use of the expression for \(R_0\) give

$$\begin{aligned} \limsup _{t\rightarrow \infty }\bar{x}(t)\le \left( 1+\frac{ r (1-\sigma )\theta }{\alpha +\mu }\right) x^{*}. \end{aligned}$$

We conclude that the average number of susceptibles on the long run is always less than or equal to the equilibrium value times a constant. \(\square \)

5 Discussion

Disease patterns generated by communicable diseases have been documented for various pathogens across multiple levels of organization and spatial scales over the past two centuries. Recurrent epidemic outbreaks like those generated by measles or influenza are of extreme biological, epidemiological and health public importance. It is therefore not surprising that efforts to identify and assess the importance of mechanisms responsible for recurrent epidemic patterns have been carried out for over a century with the aid of mathematical models. The impact of the continuous evolution of influenza genetic diversity driven by antigenic “drift,” the driver of strain heterogeneity and antigenic “shift,” the generator of subtype variability across levels of organization is one of the most challenging evolutionary biology problems due to its implications on the health and lives of more than seven billion people (Thacker 2005). The fact that influenza lives in avian and mammal populations with genetic recombination and human local, regional and global mobility playing a major role on its local, regional and global dynamics provides one of a most challenging convergence research landscapes at the interface of the life, social, computational and mathematical sciences. Influenza dynamics live in a changing environmental landscape that it is altered in response to seasonality, delays driven by human interventions (quarantine/isolation), human population structure and heterogeneity, behavioral responses, public health policy and technological advances. (Castillo-Chavez et al. 1988, 1989; Valle et al. 2005; Hethcote 2000; Hethcote et al. 2002; Nuño 2005).

Our work focuses on the role of host quarantine/isolation within a broad of epidemiological framework. Our work is motivated by our interest on the mathematical resilience of influenza dynamics, with emphasis on the role of intervention policies that are not carried out effectively, imperfect quarantine. The work is theoretical and so the effectiveness of quarantine is measured by a single parameter \(\sigma \in [0, 1]\). The mathematical analysis shows that the model has a disease-free equilibrium which is globally stable whenever control is effective, that is, when \(R_0 < 1\) and otherwise it is unstable. Furthermore, it is shown that this model has a unique endemic equilibrium whenever \(R_0 > 1\) with the disease being uniformly persistent as long as \(R_0 > 1\).

Past research has studied the mathematical impact of quarantine/isolation on disease dynamics whenever \(R_0 > 1\). It has been shown that such public health interventions support, within appropriate regimes of parameter space (see Fig. 2), the existence of stable periodic solutions (recurrent outbreaks); that is instability as parameters are varied. These results are not robust as the quarantine policy is varied within the epidemiological parameter regime that will support them when quarantine is perfect. Our results provide strong support for the existence of periodic solutions (via Hopf bifurcation) as quarantine effectiveness (\(\sigma \)) varies but only when it is executed close to perfection (results verified numerically via MATCONT, Fig. 3). Our model assumes that infective individuals gain full immunity after recovery and so the results in Fig. 4 suggest that interepidemic periods are in the range of 9.5–11 years when the effectiveness of quarantine \(\sigma \) is slightly smaller than 1. As the level of inefficiency increases, imperfect quarantine, damped periodic solutions arise (see Fig. 5). Note that the values for the reproduction number \(R_0\) inside the Hopf Bifurcation curves in Fig. 2 (right) are chosen between 1 and 16, which include estimated influenza values of 1 and 2.5 (Nishiura et al. 2009, 2010; Nuño 2005). The parameter values \(\mu =1/3650\), \(\gamma =0.5\), and \(\theta =1, 2, 4\) and 6 per week used for Fig. 2 (right) are plausible, since they correspond to an average lifetime \({1}/{\mu }\) of 3650 weeks, about 70 years; an average infectious period \({1}/{\theta }\) before quarantine of 0.15 to 1 week; and an average infectious period \({1}/{\gamma }\) before going to the removed class of 2 weeks. Note that the Hopf bifurcation curves in Fig. 2 (right) are almost independent of the value of \(\gamma \) in the range between 0.1 and 2, but are strongly dependent on the value of \(\theta \). From a practical point of view, it is likely that the quarantine period \({1}/{\alpha }\) would be chosen to be at least as large as the average infectious period \({1}/{\gamma }\), so that \(\alpha \le \gamma \).

The issue of what epidemiological models actually support sustained oscillations is of mathematical and biological interest. The data and time series available are not long enough to in fact determine whether or not what we are seeing are the results of periodic dynamics or damp oscillations. Nevertheless, it is important from a theoretical epidemiological perspective to know what are the mechanisms that stabilize or destabilize disease dynamics under appropriate parameter regimes. The results of this paper address the mathematical robustness of such models. We show that simple epidemiological models can’t generate sustained oscillations as a result of quarantine policies, since their implementation at larger population scales will be in general impossible due to errors, human behavior and lack of resources.

Theoretical results can impact public policy. For example, the problems raised by the distribution and misuses of antibiotics or by nosocomial infections have been documented and models have been developed to study the impact of errors in drug administration with the impact of those results closely tied in to the policy objective (Chow et al. 2011; Lipsitch et al. 2000). And so the value of this contribution is tied in to the fact that it uses parameters that are common to influenza outbreaks and it shows, perhaps clearly for the first time, that human decisions, policy effectiveness can shift disease dynamics from apparently unstable (ups and downs) to predictable, that is, endemic.