1 Introduction

Increasingly cities around the world are building urban emergency shelters because of a heightened awareness of the potential for natural hazards and disasters, such as earthquakes, floods, typhoons, and tsunamis (Xu et al. 2007; Tai et al. 2010; Bashawri et al. 2014). With the rapid development of the Chinese economy and the urbanization process, urban populations have greatly increased. Natural hazards and disasters, as well as technological disasters, can cause great loss of lives and properties (Wei et al. 2012). This threat requires effective disaster prevention, mitigation, and preparedness in cities. One of the most important tasks of disaster management is the planning and construction of urban emergency shelters that guarantee public security in cities (Tong et al. 2012). Many investigations have been done in the field of shelter selection and evaluation. Tai et al. (2010) proposed a method for analyzing road network factors and evacuation choices of residents in the case of an earthquake. Liu et al. (2011) used the 2008 Wenchuan Earthquake as an example for analyzing and applying the principles of emergency shelter selection for a disastrous earthquake. The analysis results in their studies can be utilized by the government as a decision-support tool for decision makings in earthquake recovery and reconstruction programs. Kılcı et al. (2015) explored the need to locate temporary shelter areas in an earthquake disaster. They introduced a new methodology for selecting the location of temporary shelter sites for Kartal, a district of Istanbul, Turkey. These recent studies have demonstrated that urban emergency shelter assessment work can better help evacuate citizens in a disaster.

To conduct the spatial assessment of the location-allocation of shelters, a number of methods and models have been proposed globally. Dalal et al. (2007) considered the stochastic nature of hurricanes by generating different scenarios and introduced shelter location planning under hurricane conditions. Alçada-Almeida et al. (2009) employed a multiobjective approach to locating shelter sites and identifying evacuation routes. Pan (2010) presented the shelter site location problem after a disaster by formulating two models that are variations of a maximum set-covering problem. Li et al. (2012) proposed a bi-level optimization method for selecting the location of shelter sites after a hurricane. Coutinho-Rodrigues et al. (2012) developed a multiobjective approach to identifying evacuation paths and shelter locations for urban evacuation planning based on GIS technology. Chu and Su (2012) established a fixed seismic shelter evaluation system that comprises three first-level indices generated using the analytic hierarchy process (AHP), entropy methods, and the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) method. Nappi and Souza (2015) provided criteria and important aspects that need to be addressed by a multi-criteria model for risk management, specifically with respect to moving and temporarily sheltering the residents affected by a disaster. Qualitative and quantitative aspects were identified and summarized into 10 criteria and hierarchically structured in their study. All of these studies had the same objectives, that is to maximize the population covered, minimize the distance between shelters and residents, and select the most reliable set of emergency shelters by considering the safety of these shelters.

Optimal spatial distribution of urban shelters must be based on a reasonable estimation of population in an area or region. The urbanization process has made the structure of cities more complex (Jia et al. 2014). The study of urban population distribution has become more critical in disaster management and risk assessment. Determining population exposure in a disaster is regarded as one of the prerequisite tasks of risk assessment (Freire et al. 2013). Wood et al. (2014) examined how post-disaster redevelopment after a catastrophic tsunami may have changed the vulnerability of coastal populations to future tsunamis. Masuya et al. (2015) assessed the spatial distribution of flood shelters and vulnerable residential units with respect to flood hazards. They attempted to identify potential flood shelter locations based on vulnerable housing units and estimated the potential population served by the shelters. Zhang et al. (2013) also considered population vulnerability distribution to optimize the population evacuation scenarios and to improve the efficiency of evacuations. These studies indicated that the description and mapping of population distribution are basic and indispensable steps for disaster management, shelter selection, and emergency evacuations. Furthermore, daytime population distribution and density in urban areas are very different from the nighttime situation (Ara 2014). Freire (2010) used a dasymetric mapping approach to refine population distribution in Portugal. He separated population into nighttime (residential) population, daytime residential population, daytime worker and student population, and ambient population. Sample applications were then presented in the context of emergency management, such as examples of technological hazards, natural hazards, and terrorist attack. Freire et al. (2013) considered the time dependence of population exposure with respect to tsunami threat and developed high-resolution daytime and nighttime population distribution maps. These were combined with a tsunami hazard map, information on infrastructure, and terrain slope to assess evacuation scenarios.

This article presents a spatial distribution assessment framework for urban emergency shelters based on the multi-criteria method. The purpose of the study was the integration of three main aspects in the framework: (1) a high-precision population estimation that can quantify the numbers of different kinds of people in different buildings and at other locations; (2) a multi-criteria sensitivity analysis that can reduce the uncertainty in criteria weighting and generate an improved spatial distribution assessment; and (3) a spatial distribution assessment of urban shelters in the daytime and at nighttime, respectively, that can help make better location-allocation decisions for shelters. The assessment results generated from this framework can reveal the spatial satisfaction differences of sheltering services for the residents in the study area and further support the spatial allocation work for urban shelters. Section 2 introduces the study area. Section 3 presents the assessment process in accordance with the proposed framework, and Sect. 4 presents the shelter distribution evaluation results for the selected scenarios.

2 Study Area

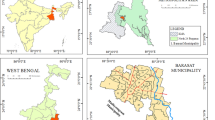
Jing’an District is one of the central urban districts of Shanghai Municipality, China (Fig. 1). It has 14 subdistricts, which covers an area of 37.37 km2. Before it was merged with Zhabei District in 2015, it only had five subdistricts. The study area covers these five subdistricts, with an area of 7.62 km2 (7.57 km2 of land area and 0.05 km2 of water area). As one of the downtown districts in Shanghai, Jing’an District has a business zone represented by Westgate Mall, Citic Square, and Plaza66, and a hotel zone of upscale hotels, such as the Jing’an Hilton Hotel, the Shanghai JC Mandarin, and the Shanghai International Equatorial Hotel. The business zone and the hotel zone are in Jing’ansi and West Nanjing Road subdistrict. Contemporary district functions and status combine a high concentration of talents, materials, capital, and information, making the district an ideal destination for investment from people both in and outside of China.

Fig. 1
figure 1

Location of Jing’an District in Shanghai and the five subdistricts of the study area

Full size image

At the end of 2010, there were 246,788 registered permanent residents in the five subdistricts. But until 2014, there was only one existing urban shelter and another under construction in all of Jing’an District. Considering the large residential and working population of Jing’an District, it is urgent to build more shelters. Selecting shelter sites and evaluating the spatial distribution of urban shelters in Jing’an District are essential preconstruction steps. Optimal distribution and capacity of urban shelters are vital to minimizing casualties and economic losses from disasters.

3 The Assessment Process

The assessment framework illustrated in Fig. 2 was designed in this study to evaluate the sheltering services of urban emergency shelters. The input data include land use, population, road network, and the population capacity of shelters. These four types of data were integrated to generate the criteria layers for the spatial distribution assessment of shelters. The criteria layers include the supply–demand ratio of shelters, the service distance of shelters, the daytime or nighttime population distribution, the distance from high buildings and the distance to main roads. The layers were integrated using the AHP method to obtain the criteria weights. To reduce the uncertainty in the AHP analysis, a weight sensitivity analysis was conducted to confirm the decision maker perceptions in their assignment of the AHP pairwise matrixes. The spatial distribution assessment results in two satisfaction maps were generated for daytime and nighttime scenarios in order to make the evaluation process more comprehensive. A case study applying the framework was conducted in the five subdistricts of Jing’an District.

Fig. 2
figure 2

Evaluation framework for the spatial distribution of urban emergency shelters

Full size image

3.1 Data Collection and Processing

To generate the criteria layers for the spatial distribution assessment, different spatial data were acquired and preprocessed.

3.1.1 Land Use Data

Land use data were interpreted from the 2013 high-resolution aerial images (0.25 m resolution) of Shanghai. In 2012 the Ministry of Housing and Urban–Rural Development of China published the Classification of Urban Land Use and Planning Standards of Development Land (CULSPDL, GB50137-2011) (Wang et al. 2012). In this document, a new “town and country land classification system” was added and the categorization of urban development land was optimized. The land use classification in the HAZUS (Hazards U.S.) model developed by FEMA (Federal Emergency Management Agency of the United Stated) (Ploeger et al. 2010; Neighbors et al. 2012; Dinitz and Taketa 2013; Subramanian et al. 2013) can help make disaster risk evaluation better. Based on the CULSPDL and the land classification standard of the HAZUS model, we introduced a revised urban land categorization. The land use types in this study are listed in Table 1, and Fig. 3 shows the land use map of the case study area. Some land use types (Type Code II) can be further broken down into subtypes (Type Code III), but these are not listed in the table.

Table 1 Land use classification system used for the Shanghai case study
Full size table
Fig. 3
figure 3

Land use in the study area in Jing’an District in downtown Shanghai

Full size image

3.1.2 Population Data

Population distribution is an important topic in disaster risk research. Various approaches have been introduced to simulate high-resolution spatiotemporal population distribution, such as the population-employment ratio model (Choi et al. 2014), surface model (Lloyd and Nejad 2014), local spatial correlation analysis (Shiode et al. 2014), and the LIDAR-based volume model (Yu et al. 2010; Lwin and Murayama 2011; Hu et al. 2015). Recent studies involved specified land use data in the estimation of population, such as vegetation types (Siméoni and Lebot 2012), road networks (Quinn 2013), and greenbelts (Jun 2012). These studies found that population distributions have a remarkable relation to land use types. At nighttime, for example, most urban residents are in residential buildings, and in the daytime, employees are in office buildings and other working places. Building-specific population data are often not available for public use (Lwin and Murayama 2011). But statistical data of population at the level of census tracts or districts may be distributed into different land uses to generate more accurate spatial population distribution or population density data.

Nighttime population and daytime population are considered in this study. Nighttime population distribution was based on the Sixth National Census of Shanghai in 2010 (Shanghai Bureau of Statistics 2011). The census bulletin published the information of registered permanent residents. But it did not consider population such as shoppers and tourists (Qi et al. 2015). In this study, floating population and random population were not included in nighttime population because the population distribution is relatively stable at nighttime. Most shops and scenic spots are closed. There are few people moving around. Random population exists in the daytime, that is people who appear randomly in various places, such as shoppers, guests, tourists, and hospital visitors and patients (Qi et al. 2015). The statistical data of total random population were acquired from the Shanghai Jing’an Statistical Yearbook 2011 (The Compiling Committee of Jing’an Yearbook 2011) and the distribution was acquired by field surveys. The field surveys were conducted during 2 months in 2014. People in different places, such as plazas, markets, scenic spots, hospitals, and green spaces were counted in the morning, at noon, and in the afternoon. Because of the temporal variability of these distributions, an annual mean value was calculated for assessing total random population.

Population size and age structure data for each subdistrict and residential community can be obtained from the census. For a precise assessment of the spatial variability of shelters, an accurate population estimation for each residential building is desirable. Lwin and Murayama (2009) introduced two building population estimation methods: (1) an areametric method that does not require information on the number of building floors; and (2) a volumetric method that requires information on the number of floors. The latter is suitable for high-rise buildings, especially in central urban districts (Lwin and Murayama 2011). Equation 1 was utilized to estimate the nighttime population of a residential building by adapting the volumetric method.

$${\text{Pop}}_{{{\text{B}}(n)}} = {{{\text{Pop}}_{{{\text{C}}(k)}} \cdot {\text{A}}_{{{\text{B}}(n)}} \cdot {\text{F}}_{{{\text{B}}(n)}} } \mathord{\left/ {\vphantom {{{\text{Pop}}_{{{\text{C}}(k)}} \cdot {\text{A}}_{{{\text{B}}(n)}} \cdot {\text{F}}_{{{\text{B}}(n)}} } {\left( {\sum\limits_{i = 1}^{M} {{\text{A}}_{{{\text{B}}(i)}} \cdot {\text{F}}_{{{\text{B}}(i)}} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{i = 1}^{M} {{\text{A}}_{{{\text{B}}(i)}} \cdot {\text{F}}_{{{\text{B}}(i)}} } } \right)}}\,,\quad {\text{Pop}}_{\text{nighttime}} = \sum\limits_{k = 1}^{K} {{\text{Pop}}_{{{\text{C}}(k)}} } = \sum\limits_{n = 1}^{N} {{\text{Pop}}_{{{\text{B}}(n)}} }$$
(1)

where PopB(n) is the population of the nth residential building; Popnighttime is the total residential population at nighttime in the study area; PopC(k) is the residential population in the census tract (community) where the nth residential building is located (the census tract is the kth census tract in the study area); AB(i) is the footprint area of the ith residential building; FB(i) is the number of floor levels of the ith residential building; M is the number of residential buildings in a community; N is the number of total residential buildings in the study area; K is the number of census tracts (communities) in the study area. The value of PopC(k) was obtained from the Sixth National Census of Shanghai (Shanghai Bureau of Statistics 2011).

The estimation of population in the daytime is more complex than that at nighttime. Qi et al. (2015) divided population into home population, pendulum population, and random population. Home population refers to people who are mostly at home in the daytime, including the elderly, preschool children, and the unemployed. Pendulum population refers to people who regularly go to their workplace (or school) during the daytime and come back home at night. Random population refers to people who appear randomly in places, such as hospital visitors and patients, shoppers, guests, and tourists. Based on the Qi et al. (2015) classification method, we divided daytime population into four types: (1) residential population; (2) working population; (3) students; and (4) random population (customers, tourists, and patients). The population estimation is based on the land use data, which can be expressed by Eq. (2):

$${\text{Pop}}_{\text{daytime}} = \sum\limits_{n = 1}^{N} {{\text{Pop}}_{{{\text{Bd}}(n)}} } + \sum\limits_{m = 1}^{M} {{\text{Pop}}_{{{\text{W}}(m)}} } + \sum\limits_{l = 1}^{L} {{\text{Pop}}_{{{\text{S}}(l)}} } + \sum\limits_{k = 1}^{K} {{\text{Pop}}_{{{\text{CT}}(k)}} }$$
(2)

where Popdaytime is the total residential population in the daytime; PopBd(n) is the daytime population of the nth residential building; PopW(m) is the working population of the mth working building or place; PopS(l) is the number of students of the lth school or university; PopCT(k) is the number of customers, tourists, patients of the kth green space, shopping mall, plaza, or hospital.

Residential population in the daytime mainly includes the elderly and preschool children (Qi et al. 2015). The elderly and preschool child population of each census tract (community) can also be obtained from census data. Therefore, a similar calculation method to the nighttime residential population estimation (Eq. 1) can be utilized for the residential population of each residential building in the daytime. PopBd(n) in Eq. (2) can be estimated by Eq. (3):

$${\text{Pop}}_{{{\text{Bd(}}n )}} = {{{\text{Pop}}_{\text{Cd}} \cdot {\text{A}}_{{{\text{B}}(n)}} \cdot {\text{F}}_{{{\text{B}}(n)}} } \mathord{\left/ {\vphantom {{{\text{Pop}}_{\text{Cd}} \cdot {\text{A}}_{{{\text{B}}(n)}} \cdot {\text{F}}_{{{\text{B}}(n)}} } {\left( {\sum\limits_{i = 1}^{M} {{\text{A}}_{{{\text{B}}(i)}} \cdot {\text{F}}_{{{\text{B}}(i)}} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{i = 1}^{M} {{\text{A}}_{{{\text{B}}(i)}} \cdot {\text{F}}_{{{\text{B}}(i)}} } } \right)}}$$
(3)

where PopCd is the residential population of the elderly and preschool children. Limited by the data availability of the study area and considering the situation in China, PopCd in this study includes people age 5 and younger and age 61 and older in each census tract (community). The other parameters are the same as Eq. (1).

The working population was obtained from the Second National Economic Census of Shanghai (Shanghai Bureau of Statistics 2010) where all organizations and companies located in the study area can be found, including their addresses and the number of employees of each organization/company. The location of an organization or company was determined by its address using the geocoding function in GIS. If there are several organizations or companies at a single address, such as in a business building, the numbers of employees were summed up. The calculation equation is:

$${\text{Pop}}_{{{\text{W(}}m )}} = \left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{I} {{\text{E}}_{i} } ,\;{\text{if}}\;\sum\limits_{i = 1}^{I} {{\text{E}}_{i} } < {\text{LimitPop}}} \\ {{\text{LimitPop}},\;{\text{if}}\;\sum\limits_{i = 1}^{\text{I}} {{\text{E}}_{i} } \ge {\text{LimitPop}}} \\ \end{array} } \right.$$
(4)

In Eq. (4), E i is the number of employees of the ith organization/company located in the mth working place in the study area. LimitPop is the maximum number of people in a working building. It is an empirical value estimated during the field surveys (in this study, LimitPop is equal to 2500). Among the more than 10,000 companies and organizations registered in the study area, there is a large number of big companies and interregional organizations whose employees work in offices outside of this district as well. It is very difficult to determine the number of people working regularly in these offices. Therefore, LimitPop was used to limit the maximum population in a working building/place at any given time to make population estimation more reasonable.

Data for PopS(l) were collected from the education department of Shanghai (Education Bureau of Jing’an District 2010). PopCT(k) was acquired from the Shanghai Jing’an Statistical Yearbook 2011 (Compiling Committee of Jing’an Yearbook 2011) and the field surveys. Samples were obtained to estimate the average population density of green spaces, plazas, and hospitals. The population of each green space, plaza, or hospital can be estimated by Eq. (5):

$${\text{Pop}}_{{{\text{CT(}}k )}} = \left( {{{\sum\limits_{i = 1}^{I} {{\text{Pop}}_{{{\text{Sample(}}i )}} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{I} {{\text{Pop}}_{{{\text{Sample(}}i )}} } } {\sum\limits_{i = 1}^{I} {{\text{A}}_{{{\text{Sample(}}i )}} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{I} {{\text{A}}_{{{\text{Sample(}}i )}} } }}} \right) \cdot {\text{A}}_{{{\text{CT}}(k)}}$$
(5)

where PopSample(i) is the ith population sample of green spaces, plazas, or hospitals, ASample(i) is the area of the ith sample; ACT(k) is the area of the kth green space, plaza, or hospital. We selected 20 green spaces, 10 plazas, and 10 hospitals to sample the population. The population sample was taken in the morning, at noon, and in the afternoon for 7 days (5 workdays and 2 weekend days). PopSample(i) was assigned the average value of all sampled population of these places at different times.

Using the methods and equations above, the population distribution of the study area was obtained (Fig. 4). The daytime population distribution differed significantly from the nighttime population distribution. At night, more people were located in the Caojiadu and Jiangning Road subdistricts, because there are more residential areas in these two subdistricts, especially newly built residential areas. Most residential buildings in the new residential areas have over 10 floors, and the population densities in these areas are higher than in older neighborhoods. In the Jing’ansi and West Nanjing Road subdistricts, most residential buildings were constructed before the 1950s with less than five floors. The residential population densities there are lower at nighttime than in the other subdistricts.

Fig. 4
figure 4

Daytime and nighttime population of the study area in Jing’an District in downtown Shanghai

Full size image

Population distribution in the daytime shows great variations. Jing’ansi and West Nanjing Road subdistricts have a lot of working people in their central business districts. Compared with the nighttime population, the daytime population increases by 39.2% in the study area as a whole, but the daytime populations in Jing’ansi and West Nanjing Road subdistricts are 139.7 and 147.7% higher than the nighttime populations. The daytime population distributions of the other three subdistricts also have great variations, although the total numbers of people of the subdistricts do not appear to be much different from those at nighttime.

3.1.3 Road Data

Road data in line format were interpreted and extracted from the land use data of the study area and stored in a feature dataset in ESRI Geodatabase. A network dataset was created based on the road line data to support network analysis, such as road distance measurements, service area generation, and service circle designation.

3.1.4 Shelter Site Selection and Shelter Population Capacity Calculation

In the downtown area of the city of Shanghai, land use is under great pressure. Considering the circumstances of the current land use, this study chose 29 green spaces and squares, each of which has an area more than 2000 m2, to be potentially available shelters (Fig. 5a) because these lands can be easily transformed into urban shelters at a lower cost. It was assumed that shelters have been built at these sites both for normal and emergency uses and will be opened in a disaster or emergency situation. The satisfaction assessment of the spatial distribution of shelters is based on these assumed shelter locations. The population capacities of the potentially available shelter sites correlate with the areas of these sites. The equation for the capacity estimation is:

Fig. 5
figure 5

Criteria layers for the spatial distribution of urban shelters in the study area in Jing’an District in downtown Shanghai

Full size image
$${\text{C}}_{\text{S}} = {S \mathord{\left/ {\vphantom {S {\text{Apc}}}} \right. \kern-0pt} {\text{Apc}}}$$
(6)

where S is the covered area of a shelter, Apc is the required minimum area per capita for a shelter. The value of Apc is 1.5 m2 in this study, which was taken from the Emergency Shelters Plan in the Central City of Shanghai (2009) and the Shanghai Construction Code of Urban Green Emergency Disaster Mitigation Shelter (Draft for Discussion) (Dai et al. 2013).

3.2 Criteria Layers

Five criteria layers were set for the spatial distribution assessment, including the daytime or nighttime supply–demand ratio of shelters (SDR), service distance of shelters (SD), daytime or nighttime population (DP or NP), distance from high buildings (BD), and the distance to main roads (RD). These criteria were selected based on expert opinion, literature review (Cheng and Yang 2012; Soltani et al. 2014), and the data availability for the study area. The SDR criteria layer is calculated by Eq. (7):

$${\text{SDR}} = {{C_{S} } \mathord{\left/ {\vphantom {{C_{S} } {{\text{Pop}}_{\text{SA}} }}} \right. \kern-0pt} {{\text{Pop}}_{\text{SA}} }}$$
(7)

where C S is population capacity of a shelter, PopSA is population in the service area of the shelter. The service areas of the shelters are generated by network analysis in ArcGIS based on road data. Overlaying daytime or nighttime sheltering population data with the service areas of the shelters, the number of sheltering people in each shelter can be acquired.

To generate a continuous distribution of population in the daytime and at nighttime, kernel density estimation (Botev et al. 2010)—a fundamental spatial smoothing method—was utilized. The road dataset was compiled and imported into ArcGIS software to generate a road network dataset. Integrating the road network with the locations of the shelters, a service distance map of the shelters was generated based on the ArcGIS Network Analyst module. Table 2 gives the threshold values of the criteria for each of the five evaluation classes. The threshold values were determined mainly based on local expert knowledge and the field surveys. We also referred to the literature (Liu et al. 2011; Tong et al. 2012; Ye et al. 2012) to help ascertain some values of the criteria, such as SD and BD. Spatial data of criteria datasets were classified into five classes—highly satisfied (S1), medium–high satisfied (S2), moderately satisfied (S3), marginally satisfied (S4), and unsatisfied (S5)—and converted into integer raster layers based on Table 2. The criteria layers in raster format are shown in Fig. 5.

Table 2 Criteria for the spatial distribution evaluation of urban shelters in the study area in Jing’an District in downtown Shanghai
Full size table

3.3 Analytic Hierarchy Process (AHP) and Weight Sensitivity Analysis

The analytic hierarchy process has been widely used in various domains to solve multi-criteria evaluation problems (Saaty 1977; Chen et al. 2007; Ohta et al. 2007; Chen et al. 2010; Chen and Paydar 2012). It has also been utilized in the field of disaster risk assessment and management (Zhang and Wang 2011; Yang et al. 2012; Orencio and Fujii 2013; Chen et al. 2015). But one of the main shortcomings of this method is that it is unable to address the uncertainty and the imprecision of the decision makers in generating the pairwise comparison matrixes. Among all sources of uncertainty, such as data processing, criteria selection, and threshold determination, criteria weight is regarded as the greatest factor contributing to the uncertainty of AHP. Therefore, it is important to conduct a sensitivity analysis for criteria weights to help decision makers ascertain their preferences of criteria and reduce the uncertainty of the assignments of criteria weights.

In this study, a one-at-a-time (OAT) based AHP weight sensitivity analysis method, as proposed by Chen et al. (2013), was utilized to verify the criteria weighting results. The method can estimate criteria weight sensitivity by changing the relative importance scales between criteria in an AHP pairwise comparison matrix (PCM). The OAT technique alters the value of one element in the PCM at a time without changing other elements. The change of element value is in accordance with a scale of intensity of importance (IOI), which represents relative importance between each pair of criteria. The sensitivity analysis process is divided into four steps:

  1. (1)

    Select an element to be estimated from the PCM according to the row number and column number.

  2. (2)

    Set the changing range for the element based on the base element value. The changing range is a user-defined changing radius (R), which is a threshold to decide how many IOI values will be examined in the sensitivity analysis. The equation to select a set of IOIs for the changing range of element values is (Chen et al. 2013):

    $${\text{CREV}}(Base\_EV,R) \, = \, \{ IOI \, (i) \, |{\text{ Index}}_{B} {-}R \le i \le {\text{ Index}}_{B} + R\,{\text{and }}0 \, \le i \le \, 16\}$$
    (8)

    where Base_EV is the base element value; Index B is the index of the IOI in Eq. (9) whose value is equal to Base_EV; R is a buffer threshold that restricts the upper and lower bounds of IOI selection.

    $${\text{IOI}}(i) = \left\{ {\begin{array}{*{20}l} {(9 - i )^{ - 1} ,\,\, i < 8} \\ {1,\quad \quad\quad i = 8} \\ {i - 7,\quad\quad i > 8} \\ \end{array} } \right.\quad i = 1,\;2,\;3,\; \ldots ,\;16$$
    (9)
  3. (3)

    When changing the element value according to the IOI in CREV (Base_EV, R), the weights of all criteria will be recalculated and the consistency ratio (CR) of the PCM will be checked. If the CR checking is passed, a new assessment map will be generated, or the current PCM will be regarded as unqualified. This procedure is a loop until all the elements in CREV (Base_EV, R) have been tested.

  4. (4)

    Summarize the sequence of assessment maps and generate a relative summary statistics table that includes weight values, cell numbers at different ranking levels, and changes of cells between different ranking levels.

In this study, a base PCM was generated by expert initial opinion (Table 3). All elements in the AHP PCM were then picked to check the weight sensitivity. The weight sensitivity analysis of the element that compared SDR and DP was selected as an example among the total number of 10 tables. The base value of the element is 2. R in Eq. (8) was set as 4. Therefore, CREV(2, 4) = {1/4, 1/3, 1/2, 1, 2, 3, 4, 5, 6}. Corresponding to the IOIs in this changing range, a summary table was generated (Table 4). In the table, detailed information, including the IOI, weight values of criteria, cell numbers of classes (S1–S5), and changes in cell numbers between two classes with the change of IOI value are listed. The assessment maps are in Fig. 6, including one base run map and eight simulation maps. The simulation maps can be compared with the base run map to detect the spatial distribution changes. Figure 6j and Table 4 show that S1 is stable despite a slight variation of the cell numbers. S2 and S4 have the most significant change in area. The change of the spatial pattern can also be observed from Fig. 6a–i. The areas of S4 and S5 are clearly enlarged, especially in the western and northern regions of the study area, while S1–S3 have different degrees of reduction. Therefore, sensitivity analysis can provide information on the stability of spatial distribution assessment results, which can help stakeholders to reduce uncertainty in decision making.

Table 3 Base pairwise comparison matrix of AHP for five criteria weighting
Full size table
Table 4 Example of a summary table generated from the nine weight sensitivity analysis runs for the element of SDR to DP in satisfaction assessment, showing the eight simulation runs plus the base run (bold)
Full size table
Fig. 6
figure 6

Satisfaction maps of the base run and the eight simulation runs, and the cell number change of classes in simulation runs

Full size image

4 Results and Discussion

When the base PCM was generated by expert initial opinion, one or more elements may have uncertainty in value assignment. Using the OAT-based AHP weight sensitivity analysis method introduced in Sect. 3.3, the elements of the PCMs that have uncertainty in value assignment were checked and adjusted. The new element values were generated by expert opinions after a new discussion and thorough check of the uncertainty in criteria weighting. For the nighttime scenario, the element value of the base PCM that compared SDR and DP was changed from 2 to 3. For the daytime scenario, the element value that compared SD and NP was changed from 1 to 2. Thus, two final PCMs and two corresponding resultant maps were generated for nighttime and daytime scenarios, respectively (Fig. 7). The spatial satisfaction degree of the sheltering services for the residents is also classified into five classes: highly satisfied (S1), medium–high satisfied (S2), moderately satisfied (S3), marginally satisfied (S4), and unsatisfied (S5). In the resultant maps, different satisfaction levels are related to the degree of the nearby shelters satisfying the sheltering demand of citizens. If there are large S4 or S3 areas in a region, it means more shelters need to be set up in this region. The resultant nighttime satisfaction map indicates that the S5 and S4 areas are mainly distributed in the northern and eastern parts of the study area. S3 areas exist in all five subdistricts, while the S2 areas are largely in the southern and eastern parts of the study area. The S1 areas are in Jing’ansi subdistrict and in the eastern corner of Shimen Second Road subdistrict and West Nanjing Road subdistrict.

Fig. 7
figure 7

Satisfaction assessment result of the spatial distribution of emergency shelters for daytime and nighttime in the study area

Full size image

In the daytime scenario, the difficulty of sheltering is aggravated in the central and southern areas. The S3 and S4 areas increase from 19 and 23% at nighttime to 28 and 32% in the daytime. The S1 and S2 areas decrease from 19 and 27% to 11 and 17% for the whole study area. S1 does not even exist in the Jiangning Road subdistrict. The spatial satisfaction patterns in Caojiadu, Jiangning Road, and Shimen Second Road subdistricts are relatively stable. But there is a significant decreasing trend of spatial distribution satisfaction in Jing’ansi and West Nanjing Road subdistricts.

Further analysis of the spatial distribution of urban shelters can be conducted by estimating the satisfaction conditions of the buildings or land parcels (BDLPs) in which people live, work, or study in the area. Land use data and the assessment result of nighttime and daytime scenarios were overlaid to derive the statistical results illustrated in Fig. 8. In the nighttime scenario, there are 1169 BDLPs in S1 class. The numbers of BDLPs of S2 and S3 classes are 1972 and 1573, respectively. There are 1671 BDLPs in S4 class, which is about 23.5% of all the BDLPs. S5 class is of critical concern in this study because the BDLPs that are in this class have the lowest satisfaction level of urban shelter service and a higher risk in a disaster or emergency situation. In nightime, 730 BDLPs are in the S5 range. It can also be estimated from Fig. 8a that Jing’ansi subdistrict has the highest satisfaction situation while Jiangning Road and Caojiadu subdistricts have the lowest satisfaction.

Fig. 8
figure 8

Number of buildings (or land parcels) in each shelter satisfaction class in the daytime and at nighttime in the five study area subdistricts of Jing’an District in downtown Shanghai

Full size image

Figure 8b presents the satisfaction situations of BDLPs in the daytime. The BDLP numbers in S1 and S2 classes decrease to 543 and 1201, and there is no BDLP in S1 class in Jiangning Road subdistrict. Changes in proportions of BDLP numbers in S3 and S4 classes are insignificant. But the BDLP numbers of S5 class in the daytime decrease to 475. Jing’ansi subdistrict still has the highest satisfaction, but the BDLP number in S1 class is greatly reduced. Although Jiangning Road and Caojiadu subdistricts still have a serious situation, the numbers of BDLPs in S4 and S5 classes in Jiangning Road significantly decrease when compared with the nighttime scenario.

The measurement of how many people are in different satisfaction classes is also important for the spatial distribution assessment of urban shelters. With a spatial overlay of the daytime/nighttime population, the administrative divisions, and the satisfaction maps for nighttime and daytime, the statistical diagrams were generated in Fig. 9. In the nighttime scenario, only about 5.5% people of all the people in the study area are in the S1 areas. S2 and S3 areas have 19.6 and 16.3% people, respectively. More people are in the areas of S4 and S5 classes. The percentages of people in these two areas are 30.3 and 28.3%, respectively. In the daytime scenario, people in S4 class have greatly increased from 75,149 to 150,147. People in S5 and S3 areas have also increased from 40,579 and 70,365 to 72,975 and 83,529, while people in the other two classes are reduced from 13,571 and 48,574 to 9454 and 29,560, respectively. The increase of people in the S3 to S5 classes is mostly due to the population increase in West Nanjing Road and Jing’ansi subdistricts in the daytime.

Fig. 9
figure 9

Number of people in each satisfaction class in the daytime and at nighttime in the five study area subdistricts of Jing’an District in downtown Shanghai

Full size image

Preschool children and the elderly are more vulnerable than others when facing emergency and unexpected events. Their satisfaction situations are of great significance to the evaluation of the spatial distribution of urban shelters. The distribution of children and the elderly in different satisfaction classes in the daytime and at nighttime are assessed and presented in Fig. 10. The total number of children and elderly in the study area at nighttime is 62,640, in which 5.9% are in S1, 20.5% in S2, 17.3% in S3, 29.3% in S4, and 27.0% in S5 classes. Children and the elderly who are in the S4 and S5 classes need more attention. Figure 10a indicates that these people are mostly in Jiangning Road and Caojiadu subdistricts. In the daytime scenario, the distributions of children and the elderly in different satisfaction classes have changed. There are 5.8% children and elderly in the S1, 15.2% in S2, 26.9% in S3, 36.9% in S4, and 15.2% in S5 classes. Children and elderly who are in the classes of S4 and S5 are still concentrated in Jiangning Road and Caojiadu subdistricts. But more children and elderly appear in West Nanjing Road and Shimen Second Road subdistricts than in the nighttime scenario.

Fig. 10
figure 10

Number of preschool children and elderly in each satisfaction class in the daytime and at nighttime in the five study area subdistricts of Jing’an District in downtown Shanghai

Full size image

Based on the above analysis, it can be summarized that both at nighttime and in the daytime, even if all the selected potentially available shelter sites are built and open in an emergency event, they still cannot satisfy the sheltering demands of all the residents in the study area, especially in the northern and eastern parts close to residential areas and the central business district. In the nighttime scenario, the northern and eastern areas that are mainly in Jiangning Road and Caojiadu subdistricts have the lowest satisfaction situation. A large number of residents, especially children and the elderly, are in unsatisfied and marginally satisfied regions. In the daytime scenario, the low satisfaction regions expand to the central area. The situation eases slightly in Jiangning Road and Caojiadu subdistricts, but many working people are in marginally satisfied areas in West Nanjing Road subdistrict. It is urgent to build more urban shelters in the study area, especially in the northern, eastern, and central regions, to guarantee the safety of the residents. More affiliated lands of government departments and institutions need to be opened to the public and more open green infrastructure or squares need to be built in the study area to cope with disasters and other emergency events.

The above analysis proves that the method proposed in this study is not only able to map the distribution of different satisfaction regions of sheltering services, but also able to provide statistical estimation of the building and population coverage of different satisfaction regions. The satisfaction map is an important assessment of the spatial distribution of urban shelters that can be used to support further shelter location-allocation decisions. New shelters are more likely to be allocated in the unsatisfied (S4) or marginally satisfied (S3) areas, taking into consideration spatial satisfaction results in daytime and nighttime scenarios (Fig. 7) simultaneously. In big cities, it is not an easy task to build new shelters in downtown areas because there is limited land that can be allocated. Residential, commercial, and industrial lands often cannot be converted into shelters. Only some green infrastructure and squares, public management and service lands, and unused lands can be used to build new urban shelters. The satisfaction maps derived from this study are indispensable for potential shelter site selection. In practice, an objective function can be defined to derive optimized locations for new shelters. The function can have four spatial parameters: (1) the spatial scope of a candidate shelter area that contains S4 and S5 areas in the satisfaction maps; (2) a current land use map that identifies land parcels that cannot be allocated; (3) the overall satisfaction level of residents in the daytime; and (4) the overall satisfaction level at nighttime. The object of the function is to find the maximum value of the function, because the most optimal location-allocation scheme is to improve the satisfaction levels of residents to the greatest extent. Once the maximum value is found, the spatial locations of new shelters can be determined.

5 Conclusion

This study proposed a new satisfaction assessment framework of spatial distribution of urban shelters on the basis of the distribution of nighttime and daytime population. The population data acquisition relied on land use data, population census, economic census, local statistical data, and field surveys. Using a series of equations, the spatial distributions of the nighttime and daytime population were derived. Through integrating the population capacities of shelters, population distribution, and road network data, five criteria were selected to conduct a spatial distribution assessment using the AHP method. In order to reduce the uncertainty in AHP criteria weighting, an OAT-based sensitivity analysis was utilized to help the decision makers ascertain the preferences of the criteria weights. The advantage of the sensitivity analysis lies in the weight calculation compared with the traditional weight judgment method in AHP. The framework can reveal the capacity of the shelters and the spatial satisfaction in a region. It can also visualize the distribution of different satisfaction classes of sheltering services and quantitatively describe the number of buildings or land parcels, total population, and children and elderly in various satisfaction classes.

The case study showed that the framework is effective and feasible. It can be implemented in practical urban shelter evaluation and location-allocation work. The generated thematic maps can help spatially and quantitatively indicate whether the shelters can satisfy the requirements of evacuation and emergency sheltering of urban residents in different locations. Therefore, the framework developed in this study can support stakeholders (such as local government departments, including the Civil Affairs Bureau and the Department of Urban Construction Management) in making better decisions and is easy to use in other case studies. In our future work, we will pursue further quantitative evaluations in different disaster scenarios to reveal potential problems and solutions in urban evacuation and sheltering.