Skip to main content
SpringerLink
Log in

Bilinear state space systems for nonlinear dynamical modelling

  • Published:
Theory in Biosciences Aims and scope Submit manuscript

Summary

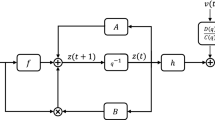
We discuss the identification of multiple input, multiple output, discrete-time bilinear state space systems. We consider two identification problems. In the first case, the input to the system is a measurable white noise sequence. We show that it is possible to identify the system by solving a nonlinear optimization problem. The number of parameters in this optimization problem can be reduced by exploiting the principle of separable least squares. A subspace-based algorithm can be used to generate initial estimates for this nonlinear identification procedure. In the second case, the input to the system is not measurable. This makes it a much more difficult identification problem than the case with known inputs. At present, we can only solve this problem for a certain class of single input, single output bilinear state space systems, namely bilinear systems in phase variable form.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Sjöberg, Q. Zhang, L. Ljung, A. Benveniste, B. Delyon, P.-Y. Glorennec, H. Hjalmarsson, and A. Juditsky, “Nonlinear black-box modeling in system identification: A unified overview,” Automatica, no. 12, pp. 1691–1724, 1995.

  2. C. Bruni, G. Dipillo, and G. Koch, “Bilinear systems: An appealing class of nearly linear systems in theory and applications,” IEEE Transactions on Automatic Control, vol. 19, pp. 334–348, Aug. 1974.

    Article  Google Scholar 

  3. R. R. Mohler and W. J. Kolodziej, “An overview of bilinear system theory and applications,” IEEE Transactions on Systems, Man and Cybernetics, vol. 10, pp. 683–688, Oct. 1980.

    Article  Google Scholar 

  4. A. Isidori, “Direct construction of minimal bilinear realizations from nonlinear input-output maps,” IEEE Transactions on Automatic Control, vol. 18, pp. 626–631, Dec. 1973.

    Article  Google Scholar 

  5. B. Hanzon and R. Peeters, “Balanced parameterizations of stable SISO all-pass systems in discrete-time,” tech. rep., Maastricht University, 1997.

  6. G. H. Golub and V. Pereyra, “The differentiation of pseudo-inverses and nonlinear least squares problems whose variables separate,” SIAM Journal of Numerical Analysis, vol. 10, pp. 413–432, Apr. 1973.

    Article  Google Scholar 

  7. M. B. Priestley, Non-linear and Non-stationary Time Series Analysis. London: Academic Press, 1988.

    Google Scholar 

  8. M. Verhaegen, “Identification of the deterministic part of MIMO state space models given in innovations form from input-output data,” Automatica, vol. 30, no. 1, pp. 61–74, 1994.

    Article  Google Scholar 

  9. P. Van Overschee and B. De Moor, “N4SID: Subspace algorithms for the identification of combined deterministic and stochastic systems,” Automatica, vol. 30, no. 1, pp. 75–93, 1994.

    Article  Google Scholar 

  10. V. Verdult, M. Verhaegen, C. T. Chou, and M. Lovera, “Efficient and systematic identification of MIMO bilinear state space models,” in Proceedings of the 37th IEEE Conference on Decision and Control, (Tampa, Florida), pp. 1260–1265, Dec. 1998.

  11. V. Verdult, M. Verhaegen, and C. T. Chou, “Identification of MIMO bilinear state space models using separable least squares,” in Proceedings of the American Control Conference, (San Diego, California), pp. 838–842, June 1999.

  12. W. Favoreel and B. De Moor, “Subspace identification of bilinear systems,” in Proceedings of MTNS 98, (Padova, Italy), July 1998.

  13. W. Favoreel, B. De Moor, and P. Van Overschee, “Subspace identification of bilinear systems subject to white inputs,” IEEE Transactions on Automatic Control, vol. 44, pp. 1157–1165, June 1999.

    Article  Google Scholar 

  14. V. Verdult and M. Verhaegen, “Subspace identification of MIMO bilinear systems,” in Proceedings of the European Control Conference, (Karlsruhe, Germany), Sept. 1999.

  15. K. K. Johnson and I. W. Sandberg, “The stability of quadratic filters,” International Journal of Circuit Theory and Applications, vol. 26, pp. 191–197, 1998.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Applied Physics, University of Twente, P.O. Box 217, NL-7500 AE, Enschede, The Netherlands

    Vincent Verdult & Michel Verhaegen

Authors
  1. Vincent Verdult
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michel Verhaegen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vincent Verdult.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Verdult, V., Verhaegen, M. Bilinear state space systems for nonlinear dynamical modelling. Theory Biosci. 119, 1–9 (2000). https://doi.org/10.1007/s12064-000-0001-9

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12064-000-0001-9

Key words

Search

Navigation