Skip to main content
SpringerLink
Log in

Nonlinear Dynamics of Slipping Flows

  • Published:
Radiophysics and Quantum Electronics Aims and scope

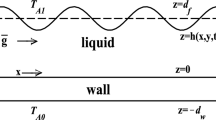
We develop a new concept for the formation of behavior features of inviscid incompressible fluids on the rigid boundary due to breaking of slipping flows. The breaking possibility is related to the compressibility of such flows due to the boundary. For two- and three-dimensional inviscid Prandtl equations, we analytically obtain the criteria for a gradient catastrophe for slipping flows. For the two-dimensional Prandtl equations, breaking occurs for both the velocity component parallel to the boundary and the vorticity gradient. The explosive growth of the vorticity gradient correlates with the appearance of a jet in the direction perpendicular to the boundary. For the three-dimensional Prandtl flows, breaking (fold formation) leads to an explosive growth for both the symmetric part of the velocity-gradient tensor and its antisymmetric part, i.e., vorticity. The blow-up generation of vorticity is possible due to the fluid suction from the slipping flow with simultaneous formation of a jet perpendicular to the boundary. These factors can be considered as a tornado-formation mechanism. Within the framework of the two-dimensional Euler equations, we numerically study the problem of the formation of increasing velocity gradients for the flows between two parallel plates. It is revealed that on the rigid boundary, the maximum velocity gradient exponentially increases with time simultaneously with an increase in the vorticity gradient according to the double exponential law. This process is also accompanied by a jet formation in the direction perpendicular to the boundary.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. N.Kolmogorov, Dokl. Akad. Nauk SSSR, 31, 538–541 (1941).

    Google Scholar 

  2. D. Chae, in: C. M. Dafermos and M.Pokorny, eds.,Handbook of Differential Equations: Evolutionary Equation, Elsevier, Amsterdam (2008), pp. 1–55.

    Google Scholar 

  3. J. D. Gibbon, Physica D, 237, Nos. 14–17, 1894–1904 (2008). https://doi.org/10.1016/j.physd.2007.10.014

    Article  ADS  MathSciNet  Google Scholar 

  4. W.Wolibner, Math. Z., 37, 698–726 (1933). https://doi.org/10.1007/BF01474610

    Article  MathSciNet  Google Scholar 

  5. T. Kato, Arch. Ration. Mech. Anal., 25, 188–200 (1967). https://doi.org/10.1007/BF00251588

    Article  Google Scholar 

  6. V. I.Yudovich, Zh. Vych. Mat. Mat. Fiz., 3, No. 6, 1032–1063 (1963).

    Google Scholar 

  7. E. A. Kuznetsov, V. Naulin, A.H.Nielsen, and J. J.Rasmussen, Phys. Fluids, 19, No. 10, 105110 (2007). https://doi.org/10.1063/1.2793150

    Article  ADS  Google Scholar 

  8. D. S.Agafontsev, E.A.Kuznetsov, and A.A. Mailybaev, Phys. Fluids, 27, No. 8, 085102 (2015). https://doi.org/10.1063/1.4927680

    Article  ADS  Google Scholar 

  9. D. S.Agafontsev, E.A.Kuznetsov, and A.A. Mailybaev, JETP Lett., 104, No. 10, 685–689 (2016). https://doi.org/10.1134/S002136401622001X

    Article  ADS  Google Scholar 

  10. D. S.Agafontsev, E.A.Kuznetsov, and A.A. Mailybaev, J. Fluid Mech., 813, R1 (2017). https://doi.org/10.1017/jfm.2017.1

    Article  ADS  Google Scholar 

  11. E. A. Kuznetsov and E. V. Sereshchenko, JETP Letters, 109, No. 4, 239–242 (2019). https://doi.org/10.1134/S0021364019040039

    Article  ADS  Google Scholar 

  12. D. S.Agafontsev, E.A.Kuznetsov, A.A.Mailybaev, and E.V. Sereshchenko, Phys. Usp., 65, No. 2, 189–208 (2022). 103367/UFNe.2020.11.048875

  13. M. E. Brachet, M. Meneguzzi, A.Vincent, et al., Phys. Fluids A, 4, No. 12, 2845–2854 (1992). https://doi.org/10.1063/1.858513

  14. E.A. Kuznetsov and V.P.Ruban, JETP Lett., 67, No. 12, 1076–1081 (1998). https://doi.org/10.1134/1.567795

    Article  ADS  Google Scholar 

  15. E.A. Kuznetsov and V.P.Ruban, J. Exp. Theor. Phys., 91, No. 4, 775–785 (2000). https://doi.org/10.1134/1.1326970

    Article  ADS  Google Scholar 

  16. E. A. Kuznetsov, JETP Lett., 76, No. 6, 346–350 (2002). https://doi.org/10.1134/1.1525034

    Article  ADS  Google Scholar 

  17. G. Luo and T. Y. Hou, PNAS, 111, No. 26, 12968–12973 (2014). https://doi.org/10.1073/pnas.1405238111

    Article  ADS  Google Scholar 

  18. A. Kiselev and V. Šverák, Ann. Math., 180, No. 3, 1205–1220 (2014). https://doi.org/10.4007/annals.2014.180.3.9

    Article  MathSciNet  Google Scholar 

  19. E. A. Kuznetsov and E. A. Mikhailov, Ann. Phys., 447, No. 2, 169088 (2022). https://doi.org/10.1016/j.aop.2022.169088

    Article  Google Scholar 

  20. E. A. Kuznetsov and E. A. Mikhailov, in: The XXth Sci. School “Nonlinear Waves 2022.” November 7–13, 2022. Nizhny Novgorod, Russia https://nonlinearwaves.ipfran.ru/lectors/prezentation/Kyznetsov_E_A.pdf

  21. W.E and B. Engquist, Comm. Pure Appl. Math., 50, No. 12, 1287–1293 (1997). https://doi.org/10.1002/(SICI)1097-0312(199712)50:12<1287::AID-CPA4>3.0.CO;2-4

  22. L. L. van Dommelen and S. F. Shen, J. Comp. Phys., 38, No. 2, 125–140 (1980). https://doi.org/10.1016/0021-9991(80)90049-2

    Article  ADS  Google Scholar 

  23. I. Kukavica, V.Vicol, and F.Wang, Adv. Math., 307, 288–311 (2017). https://doi.org/10.1016/j.aim.2016.11.013

    Article  MathSciNet  Google Scholar 

  24. L. Hong and J.K.Hunter, Comm. Math. Sci., 1, No. 2, 293–316 (2003). https://doi.org/10.4310/CMS.2003.v1.n2.a5

    Article  Google Scholar 

  25. L. Crocco, Rend. Math. Appl., 5, 138–152 (1941).

    Google Scholar 

  26. L. Crocco, Atti Guidonia XVII, 7, 118–127 (1939).

    Google Scholar 

  27. U. Frisch, Turbulence. The Legacy of A. N. Kolmogorov, Cambridge Univ. Press, Cambridge (1995). https://doi.org/10.1017/S0022112096210791

  28. N. N.Kalitkin and A. A. Belov, Dokl. Math., 88, No. 2, 596–600 (2013). https://doi.org/10.1134/S1064562413050128

    Article  MathSciNet  Google Scholar 

  29. B. G.Konopelchenko and G. Ortenzi, J. Phys. A: Math. Theor., 55, No. 3, 035203 (2022). https://doi.org/10.1088/1751-8121/ac42aa

    Article  ADS  Google Scholar 

  30. E. A. Kuznetsov, Physica D, 184, Nos. 1–4, 266–275 (2003). https://doi.org/10.1016/S0167-2789(03)00225-2

    Article  ADS  MathSciNet  Google Scholar 

  31. S. F. Shandarin and Ya.B. Zeldovich, Rev. Mod. Phys., 61, No. 2, 185–220 (1989). https://doi.org/10.1103/RevModPhys.61.185

    Article  ADS  Google Scholar 

  32. B. G.Konopelchenko and G. Ortenzi, https://arxiv.org/abs/2302.08318

Download references

Author information

Authors and Affiliations

  1. P. N. Lebedev Physics Institute of the Russian Academy of Sciences, Moscow, Russia

    E. A. Kuznetsov & E. A. Mikhailov

  2. L. D. Landau Institute of Theoretical Physics of the Russian Academy of Sciences, Chernogolovka, Russia

    E. A. Kuznetsov

  3. Skolkovo Institute of Science and Technology, Moscow, Russia

    E. A. Kuznetsov & E. A. Mikhailov

  4. M. V. Lomonosov Moscow State University, Moscow, Russia

    E. A. Mikhailov & M. G. Serdyukov

Authors
  1. E. A. Kuznetsov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. A. Mikhailov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. G. Serdyukov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. A. Kuznetsov.

Additional information

Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Radiofizika, Vol. 66, Nos. 2–3, pp. 145–160, February–March 2023. Russian DOI: https://doi.org/10.52452/00213462_2023_66_02_145

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuznetsov, E.A., Mikhailov, E.A. & Serdyukov, M.G. Nonlinear Dynamics of Slipping Flows. Radiophys Quantum El 66, 129–142 (2023). https://doi.org/10.1007/s11141-023-10281-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11141-023-10281-9

Search

Navigation