Skip to main content
SpringerLink
Log in

A Two-component Generalization of the Camassa-Holm Equation and its Solutions

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

Abstract

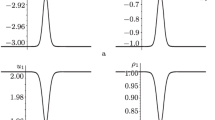
An explicit reciprocal transformation between a two-component generalization of the Camassa–Holm equation, called the 2-CH system, and the first negative flow of the AKNS hierarchy is established. This transformation enables one to obtain solutions of the 2-CH system from those of the first negative flow of the AKNS hierarchy. Interesting examples of peakon and multi-kink solutions of the 2-CH system are presented

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abenta S., Grava T. Modulation of Camassa–Holm equation and reciprocal transformations. math-ph/0506042

  2. Ablowitz M.J., Kaup D.J., Newell A.C., Segur H. (1974). The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math. 53:249–315

    MathSciNet  Google Scholar 

  3. Alber M.S., Camassa R., Fedorov Yu.N., Holm D.D., Marsden J.E. (2001). The complex geometry of weak piecewise smooth solutions of integrable nonlinear PDEs of shallow water and Dym type. Comm. Math. Phys. 221:197–227

    Article  MATH  ADS  MathSciNet  Google Scholar 

  4. Antonowicz M., Fordy A.P. (1987). Coupled K dV equations with multi-Hamiltonian structures. Physica D28:345–357

    Article  MATH  ADS  MathSciNet  Google Scholar 

  5. Antonowicz M., Fordy A.P. (1988). Coupled Harry Dym equations with multi-Hamiltonian structures. J. Phys. A21:L269–L275

    Article  ADS  MathSciNet  Google Scholar 

  6. Antonowicz M., Fordy A.P. (1989). Factorisation of energy dependent Schrödinger operators: Miura maps and modified systems. Comm. Math. Phys. 124:465–486

    Article  MATH  ADS  MathSciNet  Google Scholar 

  7. Beals R., Sattinger D.H., Szmigielski J. (2000). Multipeakons and the classical moment problem. Adv. Math. 154:229–257

    Article  MATH  MathSciNet  Google Scholar 

  8. Camassa R., Holm D.D. (1993). An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 71:1661–1664

    Article  MATH  ADS  MathSciNet  Google Scholar 

  9. Camassa R., Holm D.D., Hyman J.M. (1994). A new integrable shallow water equation. Adv. Appl. Mech. 31:1–33

    Google Scholar 

  10. Constantin A. (2001). On the scattering problem for the Camassa–Holm equation. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 457:953–970

    MATH  ADS  MathSciNet  Google Scholar 

  11. Constantin A., McKean H.P. (1999). A shallow water equation on the circle. Comm. Pure Appl. Math. 52:949–982

    Article  MathSciNet  Google Scholar 

  12. Constantin A., Strauss W.A. (2002). Stability of the Camassa–Holm solitons. J. Nonlinear Sci. 12:415–422

    Article  MATH  ADS  MathSciNet  Google Scholar 

  13. Constantin A., Strauss W.A. (2000). Stability of peakons. Comm. Pure Appl. Math. 53:603–610

    Article  MATH  MathSciNet  Google Scholar 

  14. Degasperis, A., Holm, D.D., Hone, A.N.W.: Integrable and non-integrable equations with peakons. In: Nonlinear physics: theory and experiment, II (Gallipoli, 2002), pp. 37–43, World Scientific, River Edge, (2003).

  15. Dubrovin, B., Zhang, Y.: Normal forms of integrable PDEs, Frobenius manifolds and Gromov–Witten invariants. math.DG/0108160

  16. Dubrovin, B., Liu, S.Q., Zhang, Y.: On Hamiltonian perturbations of hyperbolic systems of conservation laws, I: quasi-triviality of bi-Hamiltonian perturbations. Commun. Pure Appl. Math. (to appear) math.DG/0410027

  17. Falqui, G., On a two-component generalization of the CH equation. In: Talk given at the conference “Analytic and geometric theory of the Camassa–Holm equation and Integrable systems”, Bologna (2004)

  18. Fokas A.S. (1995). On a class of physically important integrable equations. Physica D87:145–150

    ADS  MathSciNet  Google Scholar 

  19. Fuchssteiner B. (1996). Some tricks from the symmetry-toolbox for nonlinear equations: Generalizations of the Camassa–Holm equation. Physica D95:229–243

    Article  MATH  MathSciNet  Google Scholar 

  20. Fuchssteiner B., Fokas A.S. (1981). Symplectic structures, their Bäcklund transformations and hereditary symmetries. Physica D4:47–66

    Article  ADS  MathSciNet  Google Scholar 

  21. Gu C.H., Zhou Z.X. (1987). On the Darboux matrices of Bäcklund transformations for AKNS systems. Lett. Math. Phys. 13:179–187

    Article  MATH  MathSciNet  Google Scholar 

  22. Hone A.N.W. (1999). The associated Camassa–Holm equation and the K dV equation. J. Phys. A 32:L307–L314

    Article  MATH  ADS  MathSciNet  Google Scholar 

  23. Jaulent M., Jean C. (1976). The inverse problem for the one-dimensional Schrödinger equation with an energy-dependent potential. I. Ann. Inst. H. Poincar Sect. A (N.S.) 25:105–118

    MathSciNet  MATH  Google Scholar 

  24. Johnson R.S. (2003). On solutions of the Camassa–Holm equation. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 459:1687–1708

    Article  MATH  ADS  MathSciNet  Google Scholar 

  25. Li Y.S., Zhang J.E. (2004). The multiple-soliton solution of the Camassa–Holm equation. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 460:2617–2627

    MATH  ADS  Google Scholar 

  26. Li, Y.S., Zhang, J.E.: Analytical multiple-soliton solution of the Camassa–Holm equation. Preprint 2004, J. Nonlinear Math. Phys. (to appear)

  27. Liu S.Q., Zhang Y. (2005). Deformations of semisimple bihamiltonian structures of hydrodynamic type. J. Geom. Phys. 54:427–453

    Article  MATH  ADS  MathSciNet  Google Scholar 

  28. Martĺnez Alonso L. (1980). Schrödinger spectral problems with energy-dependent potentials as sources of nonlinear Hamiltonian evolution equations. J. Math. Phys. 21:2342–2349

    Article  ADS  MathSciNet  Google Scholar 

  29. Matveev V.B., Salle M.A. (1991). Darboux transformations and solitons In: Springer series in nonlinear dynamics. Springer, Berlin Heildelberg New York

  30. McKean H. (2003). The Liouville correspondence between the Korteweg-de Vries and the Camassa-Holm hierarchies. Dedicated to the memory of Jürgen K. Moser. Comm. Pure Appl. Math. 56:998–1015

    MATH  MathSciNet  Google Scholar 

  31. McKean H. (2004). Breakdown of the Camassa–Holm equation. Comm. Pure Appl. Math. 57:416–418

    Article  MATH  MathSciNet  Google Scholar 

  32. Schiff J. (1998). The Camassa–Holm equation: a loop group approach. Physica D 121(1–2):24–43

    Article  MATH  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, People’s Republic of China

    Ming Chen, Si-Qi liu & Youjin Zhang

Authors
  1. Ming Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Si-Qi liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Youjin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ming Chen.

Additional information

Mathematics Subject Classifications (2000). 35Q53, 37K35

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, M., liu, SQ. & Zhang, Y. A Two-component Generalization of the Camassa-Holm Equation and its Solutions. Lett Math Phys 75, 1–15 (2006). https://doi.org/10.1007/s11005-005-0041-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11005-005-0041-7

Keywords

Search

Navigation