Quantum Information Transmission with Topological Edge States

Abstract

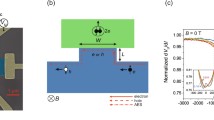
Superconducting heterostructures can host subgap states known as Andreev bound states. In topological superconducting systems, novel zero-energy Andreev states were discovered known as Majorana zero modes. Local Majorana zero modes serve as basic ingredients of topological quantum computations. To simplify manipulations, one can use chiral Majorana-fermion edge transport in gapped two-dimensional systems. Here we demonstrate how this approach can be used with continuous-spectrum edge Majorana in the Kitaev honeycomb model and discuss quantum-state transmission along the edge and its fidelity, using auxiliary external qubits as edge probes.

Appendix A: Summary of the Kitaev model

In this appendix, we provide a brief reminder of the Kitaev honeycomb spin model and its solution [10], which is essential for our analysis of the edge modes. It is defined by the Hamiltonian

$$\begin{aligned} H&= -J_x\sum _{x-\textrm{links}} \sigma _x^i \sigma _x^j -J_y\sum _{y-\textrm{links}} \sigma _y^i \sigma _y^j \nonumber \\&\quad -J_z\sum _{z-\textrm{links}} \sigma _z^i \sigma _z^j -\textbf{h}\sum _j \pmb {\sigma }^j \end{aligned}$$

(A1)

with summations over links (between sites i, j) with three different directions on the honeycomb lattice, referred to as x-, y-, and z-links, see Fig. 1. The effect of the last Zeeman term, with summation over sites j, is discussed later, while first we consider the case of no magnetic field, $\textbf{h}=0$. Analysis of this model is convenient in terms of Majorana fermionic modes: on each site i one defines four Majorana fermion operators, $c^i$, $b^i_{x,y,z}$, and the subspace of physical states in the whole Hilbert space is defined by additional constraints, which can be understood as fixing a Z$_2$ gauge: $D^i\equiv b^i_xb^i_yb^i_zc^i=+1$, while the spin operators are replaced by $\sigma ^i_\alpha =ib_\alpha ^ic^i$ with $\alpha =x,y,z$. This constraint ensures that they satisfy the standard spin algebra. Although after such fermionization the Hamiltonian appears to be of the fourth order, conservation of the relevant products $u^{jk}=i b^j_\alpha b^k_\alpha$ along all links (with $\alpha \equiv \alpha ^{ij}=x,y,z$ depending on the link direction) immediately renders the Hamiltonian quadratic in each sector of fixed $u^{jk}$, with nearest-neighbor couplings $\frac{i}{2}Ju^{jk}c_jc_k$, which allows for an exact solution [10].

In the lowest-energy sector, the system is translationally invariant [10, 51], and in the momentum representation the Hamiltonian reads:

$$\begin{aligned} H&= \frac{1}{2} \sum _\textbf{q} A(\textbf{q})_{\lambda \mu } c_{-\textbf{q}\lambda } c_{\textbf{q}\mu } \,, \end{aligned}$$

(A2)

$$\begin{aligned} A(\textbf{q})&=\begin{pmatrix} 0&{}i f(\textbf{q})\\ -i f(-\textbf{q})&{}0 \end{pmatrix}\,, \end{aligned}$$

(A3)

$$\begin{aligned} f(\textbf{q})&= 2 (J_x e^{i\textbf{qn}_1} + J_y e^{i\textbf{qn}_2} + J_z)\,, \end{aligned}$$

(A4)

where $\textbf{n}_{1,2} = (\pm 1,\sqrt{3})/2$. Here $\lambda$, $\mu$ indicate the even or odd (black or white) sublattice. For real wave vectors $\textbf{q}$ we have $f(-\textbf{q})=f^*(\textbf{q})$, but the notation in Eq. (A4) allows one to consider also complex momenta, which will be relevant near the edge. The resulting excitation spectrum is

$$\begin{aligned} \varepsilon (\textbf{q}) = |f(\textbf{q})| \,. \end{aligned}$$

(A5)

Depending on the values of the coupling constants $J_{x,y,z}$ various phases can be realized [10]. If they satisfy the triangle inequality ($|J_x|<|J_y+J_z|$, $|J_y|<|J_x+J_z|$, $|J_z|<|J_x+J_y|$), the system is in a gapless B-phase, which will be of interest to us below. In this case, the gap in the spectrum closes at two opposite values of momentum, $\pm \textbf{q}^*$, in the Brillouin zone. The existence of these nodes is topologically protected by time-reversal symmetry (since under time reversal the structure of (A3) persists). Below we assume that $J_{x,y,z}$ are in this range, and for most quantitative estimates that they are equal, where this does not change the situation qualitatively.

We are interested in a situation with a gapful 2D bulk. The gap can be opened by breaking the time-reversal symmetry with a (pseudo-)magnetic field, the last term in Eq. (A1) (its physical nature depends on a specific realization of the Kitaev model). In a weak field, $h\ll J$, the effect of the field is described, perturbatively, by the third-order contribution:

$$\begin{aligned} V^{(3)} = -\kappa \sum _{jkl} \sigma _x^j\sigma _y^k\sigma _z^l \,, \end{aligned}$$

(A6)

where summation is performed over triples jkl, in which one site is connected with the other two [10]. In this case, $\kappa \propto h^3$; more generally, if other inevitable perturbations are taken into account [28, 39], $\kappa$ is linear in h with a small prefactor and anisotropic, cf. Section 4 for more details. Thus, we obtain Majorana fermions on a honeycomb lattice with nearest- and next-nearest-neighbor couplings (J- and $\kappa$-terms), cf. Equation (48) in Ref. [10].

This term (A6) also reduces to a term, quadratic in fermions, which couples next-nearest neighbors, $\frac{i}{2}\kappa c_jc_l$, and the updated Hamiltonian (A2) involves the matrix

$$\begin{aligned} A(\textbf{q}) = \begin{pmatrix} \Delta (\textbf{q})&{}i f(\textbf{q})\\ -i f(-\textbf{q})&{}-\Delta (\textbf{q}) \end{pmatrix}\,. \end{aligned}$$

(A7)

Here $\Delta (\textbf{q}) = 4\kappa [\sin (\textbf{qn}_1) + \sin (-\textbf{qn}_2) + \sin (\textbf{q}(\textbf{n}_2-\textbf{n}_1))]$. Near the nodes $\pm \textbf{q}^*$ of the spectrum it reduces to

$$\begin{aligned} \varepsilon (\textbf{q}) \approx \pm \sqrt{3J^2\delta \textbf{q}^2 + \Delta ^2} \,, \ \delta \textbf{q}=\textbf{q} \mp \textbf{q}^* \,, \Delta =6\sqrt{3}\kappa \,. \end{aligned}$$

(A8)