Abstract
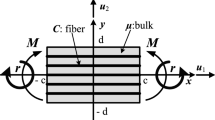
The problems on the non-uniqueness and stability of a two-family fiber-reinforced anisotropic incompressible hyper-elastic square sheet under equibiaxial tensile dead loading are examined within the framework of finite elasticity. For a two-family fiber-reinforced square sheet, which is in-plane symmetric and subjected to the in-plane symmetric tension in dead loading on the edges, three symmetrically deformed configurations and six asymmetrically deformed configurations are possible for any values of the loading. Moreover, another four bifurcated asymmetrically deformed configurations are possible for the loading beyond a certain critical value. The stability of all the solutions is discussed in comparison with the energy of the sheet. It is shown that only one of the symmetric solutions is stable when the loading is less than the critical value. However, this symmetric solution will become unstable when the loading is larger than the critical value, while one of the four bifurcated asymmetric solutions will be stable.
Similar content being viewed by others
References
Ogden, R. W. On the stability of asymmetric deformations of a symmetrically-tensioned elastic sheet. Int. J. Eng. Sci., 25(10), 1305–1314 (1987)
Reese, S. and Wriggers, P. Material instabilities of an incompressible elastic cube under triaxial tension. Int. J. Solids Struct., 34(26), 3435–3454 (1997)
Kearsley, E. A. Asymmetric stretching of symmetrically loaded elastic sheet. Int. J. Solids Struct., 22(1), 111–119 (1986)
Rivlin, R. S. Stability of pure homogeneous deformations of an elastic cube under dead loading. Quart. Appl. Math., 32(2), 265–271 (1974)
Sawyers, K. N. Stability of an elastic cube under dead loading: two equal forces. Int. J. Non-Linear Mech., 11(1), 11–23 (1976)
Ball, J. M. and Schaeffer, D. D. Bifurcation and stability of homogeneous equilibrium configurations of an elastic body under dead-load tractions. Math. Proc. Cam. Philos. Soc., 94(3), 315–339 (1983)
Ogden, R. W. Local and global bifurcation phenomena in plane-strain finite elasticity. Int. J. Solids Struct., 21(1), 121–132 (1985)
Treloar, L. R. G. Stresses and birefringence in rubber subjected to general homogeneous strain. Proc. Phys. Soc. London, 60(1), 135–142 (1948)
Hoger, A. On the dead load boundary value problem. J. Elasticity, 25(1), 1–15 (1991)
Beatty, M. F. and Pan, F. Stability of an internally constrained hyperelastic slab. Int. J. Non-Linear Mech., 33(5), 867–906 (1998)
deBotton, G. and Shmuel, G. Mechanics of composites with two families of finitely extensible fibers undergoing large deformations. J. Mech. Phys. Solids, 57(12), 1165–1181 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (No. 10772104) and the Shanghai Leading Academic Discipline Project (No. S30106)
Rights and permissions
About this article
Cite this article
Ren, Js., Cheng, Cj. Non-uniqueness and stability of two-family fiber-reinforced incompressible hyper-elastic sheet under equibiaxial loading. Appl. Math. Mech.-Engl. Ed. 34, 1513–1520 (2013). https://doi.org/10.1007/s10483-013-1763-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-013-1763-x
Key words
- two-family fiber-reinforced incompressible hyper-elastic square sheet
- non-uniqueness
- stability
- symmetric and asymmetric deformation
- equibiaxial loading