1 Introduction

Multiscale composites organized across two or more length scales are often encountered in nature, as well as in artificial materials designed to optimize specific properties (see, e.g., [10]). Relevant applications involving hierarchical systems include, but are not limited to, rocks and fracture [11], biomechanics and nanomedicine [28], poroelasticity [21], and the bone tissue [26].

Fig. 1
figure 1

Cross sections of the periodic composite: a whole material, b\(\varepsilon _1\)-structural level. c\(\varepsilon _2\)-structural level

Full size image

Multiscale modeling via suitable homogenization techniques is of crucial importance in the analysis of composite materials. On one hand, it can be exploited to obtain information concerning the coarser scale behavior of a system at hand (where experimental measurements are often easier to provide) on the basis of given microstructural properties of the finer scales. On the other hand, it can provide a deeper understanding on how to modify the microstructural arrangement of the finer scales constituents to achieve the optimal design of artificial constructs (e.g. biomimetic materials).

The most widely exploited techniques dealing with this issue in terms of mechanical properties rely on either the average field techniques, such as Eshelby-based approaches or representative volume elements formulations, as well as the asymptotic homogenization technique, see, e.g., the review [9] for a comparison. The former have been much more extensively applied to complex, hierarchical systems, although also the computational potential and theoretical reliability of the asymptotic homogenization technique has been recently investigated (see, e.g., [4, 19, 20]). In particular, the reiterated homogenization technique [1, 3, 12, 30] has been considered in the theoretical study of heterogeneous composites presenting multiple length scales. From the application point of view, an extensively discussed hierarchical hard tissue has been bone and several hierarchical modeling via homogenization and continuum micromechanics methods have been used in the analysis of its mechanical properties [7, 14, 29].

In the present work we apply the three-scale asymptotic homogenization developed in [25] (which is therein applied to hierarchical layered materials) to investigate the effective behavior of fibrous hierarchical composites. The linear elastic constitutive framework and the homogenization steps developed in [25] are briefly illustrated in Sects. 2 and 3, respectively. We apply the latter to find the effective out-of-plane shear of a hierarchical linear elastic reinforced composite assuming a square-like arrangement of uniaxially aligned cylindrical fibers at all hierarchical levels of organization. We solve the resulting anti-plane cell problems (which are depicted in Sect. 4) for isotropic and piecewise constant materials properties using results of our previous works (see e.g. [5, 6]). Our novel results (which match those computed numerically via finite elements) are presented and discussed in Sect. 5 in terms of the out-of-plane shear versus the fibers’ volume fraction. We conclude the manuscript (cf. Sect. 6) highlighting possible applications to realistic scenarios of interest, such as hierarchical modeling of fibril bundles and/or fusing mineral crystals as analyzed for example in [22] in the context of aged bone modeling.

2 The linear elastic problem

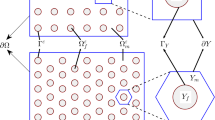
Let us denote by \(\Omega \subset \mathbb {R}^3\) a periodic composite possessing two hierarchical levels of organization (Fig. 1). The domain \(\Omega \) at the first structural level (referred to as \(\varepsilon _1\)) is assumed to be reinforced by uniaxially aligned fibers, that is \(\overline{\Omega } = \overline{\Omega }_1^{\varepsilon _1} \cup \overline{\Omega }_2^{\varepsilon _1}\), where \(\Omega _2^{\varepsilon _1} = \cup _{i=1}^N{}_{i}\Omega _2^{\varepsilon _1}\) denotes the ensemble of fibers and \(\Omega _1^{\varepsilon _1}\) is the host medium at the \(\varepsilon _1\) level. The interface between \(\Omega _1^{\varepsilon _1}\) and \(\Omega _2^{\varepsilon _1}\) is denoted by \(\Gamma ^{\varepsilon _1}\). At the second structural level (referred to as \(\varepsilon _2\)), each fiber \({}_{i}\Omega _2^{\varepsilon _1}\) is supposed to be as well reinforced by aligned fibers oriented in the same direction of the composite fiber \({}_{i}\Omega _2^{\varepsilon _1}\). Then, \({}_{i}\Omega _2^{\varepsilon _1} = \overline{\Omega }_1^{\varepsilon _2}\cup \overline{\Omega }_2^{\varepsilon _2}\), where \(\Omega _2^{\varepsilon _2} = \cup _{j=1}^M{}_{j}\Omega _2^{\varepsilon _2}\) represents the ensemble of fibers and \(\Omega _1^{\varepsilon _2}\) is the host medium at the \(\varepsilon _2\)-structural level. The interface between \(\Omega _1^{\varepsilon _2}\) and \(\Omega _2^{\varepsilon _2}\) is denoted by \(\Gamma ^{\varepsilon _2}\). At this stage, we assume that all constituents of the hierarchical composite behave as linear elastic materials with constitutive relationship for the stress tensor given by,

$$\begin{aligned} {\varvec{\sigma }}= \mathbf{ C}:{\varvec{\xi }}(\mathbf{ u}), \quad \mathrm{with}\quad {\varvec{\xi }}(\mathbf{ u}) = \frac{\nabla \mathbf{ u}+ \nabla \mathbf{ u}^T}{2}\quad \mathrm{in}\quad \Omega \end{aligned}$$

where \({\varvec{\xi }}(\mathbf{ u})\) is the elastic strain tensor and \(\mathbf{ u}(\mathbf{ x})\) is the elastic displacement at \(\mathbf{ x}= (x_1,x_2,x_3)\) with components \(u_1(\mathbf{ x})\), \(u_2(\mathbf{ x})\) and \(u_3(\mathbf{ x})\), being the components of \(\mathbf{ u}(\mathbf{ x})\) in an orthonormal cartesian vector basis. The fourth rank tensor \(\mathbf{ C}\) with components \(C_{ijkl}\) (\(i,j,k,l=1,2,3\)) is the stiffness tensor, which is assumed to be phase-wise smooth and positive definite and satisfies the standard symmetries, i.e., componentwise

$$\begin{aligned} C_{ijkl} = C_{jikl} = C_{ijlk} = C_{klij}, \quad C_{ijkl}\omega _{ij}\omega _{kl} \ge \varkappa \omega _{ij}\omega _{ij}, \end{aligned}$$

respectively, where \({\varvec{\omega }}\) is a second order symmetric tensor and \(\varkappa > 0\) is a constant. Then, ignoring inertia and volume forces, the problem in \(\Omega \) reads

$$\begin{aligned} (\mathbf{ P}^{\varepsilon }) {\left\{ \begin{array}{ll} \nabla \cdot \left[ \mathbf{ C}^{\varepsilon }:{\varvec{\xi }}\left( \mathbf{ u}^{\varepsilon }\right) \right] = 0 &{} \mathrm{in}\quad \Omega \backslash (\Gamma ^{\varepsilon _{1}} \cup \Gamma ^{\varepsilon _{2}})\\ \mathbf{ u}^{\varepsilon } = \mathbf{ u}^* &{} \mathrm{on}~\partial \Omega _d,\\ \left[ \mathbf{ C}^{\varepsilon }:{\varvec{\xi }}\left( \mathbf{ u}^{\varepsilon }\right) \right] \cdot \mathbf{ n}= \mathbf{ S}^* &{} \mathrm{on}~\partial \Omega _n, \end{array}\right. } \end{aligned}$$
(1)

where \(\mathbf{ n}\) is the outward unit vector normal to the surface \(\partial \Omega \) and \(\mathbf{ u}^*\) and \(\mathbf{ S}^*\) are the prescribed displacement and traction on \(\partial \Omega = \partial \Omega _d\cup \partial \Omega _n\) (with \(\partial \Omega _d\cap \partial \Omega _n = \emptyset \)), respectively. Moreover, continuity conditions for displacements and tractions are imposed on both \(\Gamma ^{\varepsilon _1}\) and \(\Gamma ^{\varepsilon _2}\), i.e.

(2)

where \(\mathbf{ n}_{{\varvec{\eta }}} = (n^\eta _1,n^\eta _2,n^\eta _3)\) and \(\mathbf{ n}_{{\varvec{\zeta }}} = (n^\zeta _1,n^\zeta _2,n^\zeta _3)\) represent the outward unit vectors to the surfaces \(\Gamma ^{\varepsilon _1}\) and \(\Gamma ^{\varepsilon _2}\), respectively. The operator denotes the jump across the interface between two constituents.

3 Three scales asymptotic homogenization

We consider three different scales, namely \(d_1\), \(d_2\) and L, which characterize the different structural sizes and we assume that they are well-separated, i.e.

$$\begin{aligned} \varepsilon _1 = \frac{d_1}{L} \ll 1\quad \mathrm{and}\quad \varepsilon _2 = \frac{d_2}{d_1} \ll \varepsilon _1. \end{aligned}$$
(3)

Using relation (3), two formally independent variables

$$\begin{aligned} {\varvec{\eta }}= \frac{\mathbf{ x}}{\varepsilon _1}\quad \mathrm{and}\quad {\varvec{\zeta }}= \frac{\mathbf{ x}}{\varepsilon _2} \end{aligned}$$
(4)

are introduced. Additionally, each field and material property is considered to be \({\varvec{\eta }}\) and \({\varvec{\zeta }}\) periodic [15]. As a consequence of the performed spatial scale decoupling (4) and using the chain rule, it holds that

$$\begin{aligned} \nabla \rightarrow \nabla _{\mathbf{ x}} + \varepsilon _1^{-1}\nabla _{{\varvec{\eta }}} + \varepsilon _2^{-1}\nabla _{{\varvec{\zeta }}}, \end{aligned}$$
(5)

where \(\nabla _{\mathbf{ j}}\) indicates that the derivative is performed with respect to \(\mathbf{ j}=\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }}\). We now assume that the elastic displacement \(\mathbf{ u}^{\varepsilon }\) can be represented as a power series in terms of the small parameters \(\varepsilon _1\) and \(\varepsilon _2\), namely

$$\begin{aligned} \mathbf{ u}^\varepsilon (\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }})&= \tilde{\mathbf{ u}}^{0}(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }}) + \sum _{i=1}^{\infty }\tilde{\mathbf{ u}}^i(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }})\varepsilon _2^i, \end{aligned}$$
(6)

where \(\tilde{\mathbf{ u}}^{(0)}\) is defined as

$$\begin{aligned} \tilde{\mathbf{ u}}^{0}(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }}) = \mathbf{ u}^0(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }}) + \sum _{i=1}^{\infty }\mathbf{ u}^i(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }})\varepsilon _1^i. \end{aligned}$$
(7)

Since the quantities involved vary on the \({\varvec{\eta }}\) and \({\varvec{\zeta }}\) scales, the following cell average operators are defined

$$\begin{aligned} \left\langle \bullet \right\rangle _{{\varvec{\eta }}} = \frac{1}{\left| Y\right| }\int _{Y}\bullet ~\mathrm{d}{\varvec{\eta }}\quad \mathrm{and}\quad \left\langle \bullet \right\rangle _{{\varvec{\zeta }}} = \frac{1}{\left| Z\right| }\int _{Z}\bullet ~\mathrm{d}{\varvec{\zeta }}, \end{aligned}$$

where \(\left| Y\right| \) and \(\left| Z\right| \) represent the periodic cell volumes. Here and subsequently (unless necessary), the variable dependence is dropped out for convenience.

3.1 Homogenization technique

The homogenization technique, as depicted in [25], is sketched below. First, we substitute expansion (6) into (1) and (2), and then, use the chain rule and equate in powers of \(\varepsilon _2\) “freezing” the small parameter \(\varepsilon _1\). This allows to find the effective elastic properties at the \(\varepsilon _2\)-structural level and use the results as the inputs for the problems arising at the \(\varepsilon _1\)-structural level when equating in powers of \(\varepsilon _1\). Finally, the effective coefficients of the problem are obtained. The procedure is detailed as follows:

Step 1 :

Substituting expansion (6) into (1); using result (5) and considering terms in powers of \(\varepsilon _2\).

  1. (i)

    To \(O(\varepsilon ^0_2)\)

    $$\begin{aligned}&\frac{\partial }{\partial \zeta _j}\left( C^{\varepsilon }_{ijkl}\xi ^{\zeta }_{kl}(\tilde{\mathbf{ u}}^0)\right) = 0 \quad \mathrm{in}\quad Z\setminus \Gamma _\zeta , \end{aligned}$$
    (8)
    (9)
    (10)

    with

    $$\begin{aligned} \xi ^{h}_{kl}(\mathbf{ g}) = \frac{1}{2}\left( \frac{\partial g_k}{\partial h_l} + \frac{\partial g_l}{\partial h_k}\right) , \end{aligned}$$

    where \(\mathbf{ g}\) is a vector. Since the right hand side of Eq. (8) is zero, the solvability condition is satisfied [2]. Then,

    $$\begin{aligned} \tilde{\mathbf{ u}}^{0} = \tilde{\mathbf{ u}}^{0}(\mathbf{ x},{\varvec{\eta }}) \Leftrightarrow {\left\{ \begin{array}{ll} \mathbf{ u}^0 = \mathbf{ u}^0(\mathbf{ x},{\varvec{\eta }}),\\ \mathbf{ u}^i = \mathbf{ u}^i(\mathbf{ x},{\varvec{\eta }}), \end{array}\right. } \end{aligned}$$

    i.e. the homogeneity of (8) together with (9)–(10), leads to a periodic \({\varvec{\zeta }}\)-constant solution.

  2. (ii)

    To \(O(\varepsilon _2)\) and using the fact that \(\xi ^\zeta _{kl}(\tilde{\mathbf{ u}}^{0}) = 0\),

    $$\begin{aligned}&\frac{\partial }{\partial \zeta _j}\left( C^\varepsilon _{ijkl}\xi ^\zeta _{kl}(\tilde{\mathbf{ u}}^1)\right) \nonumber \\&\quad = -\frac{\partial }{\partial \zeta _j}\bigg (C^\varepsilon _{ijkl}\bigg (\xi ^x_{kl}(\tilde{\mathbf{ u}}^0)+ \varepsilon _1^{-1}\xi ^\eta _{kl}(\tilde{\mathbf{ u}}^0) \bigg )\bigg ) \quad \mathrm{in}\quad Z\setminus \Gamma _\zeta .\nonumber \\ \end{aligned}$$
    (11)

    By the \({\varvec{\zeta }}\)-periodicity of \(\mathbf{ C}^{\varepsilon }\) and the solvability condition, Eq. (11) has a \({\varvec{\zeta }}\)-periodic solution which is unique up to an additive constant. In particular, since the problem is linear and \(\tilde{\mathbf{ u}}^{0}\) does not depend on \({\varvec{\zeta }}\), \(\tilde{\mathbf{ u}}^1\) can be written as

    $$\begin{aligned} \tilde{u}^1_i(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }}) = \tilde{\chi }_{ikl}(\mathbf{ x},{\varvec{\eta }},{\varvec{\zeta }})\tilde{U}^0_{kl}(\mathbf{ x},{\varvec{\eta }}), \end{aligned}$$
    (12)

    where

    $$\begin{aligned} \quad \tilde{U}^0_{kl} = \xi ^x_{kl}\left( \tilde{\mathbf{ u}}^0(\mathbf{ x},{\varvec{\eta }})\right) + \varepsilon _1^{-1}\xi ^\eta _{kl}\left( \tilde{\mathbf{ u}}^0(\mathbf{ x},{\varvec{\eta }})\right) . \end{aligned}$$

    The third rank tensor \(\tilde{{\varvec{\chi }}}\) is \({\varvec{\eta }}\)- and \({\varvec{\zeta }}\)-periodic, and satisfies the local problem

    $$\begin{aligned}&\frac{\partial }{\partial \zeta _j}\left( C^{\varepsilon }_{ijkl} + C^{\varepsilon }_{ijpq}\xi ^\zeta _{pqkl}(\tilde{{\varvec{\chi }}})\right) = 0 \quad \mathrm{in}\quad Z\setminus \Gamma _\zeta , \end{aligned}$$
    (13)
    (14)
    (15)

    with

    $$\begin{aligned} \xi ^h_{pqkl}(\mathbf{ G}) = \frac{1}{2}\left( \frac{\partial G_{pkl}}{\partial h_q}+ \frac{\partial G_{qkl}}{\partial h_p}\right) , \end{aligned}$$

    where \(\mathbf{ G}\) is a third rank tensor. Equations (13)–(15) constitute the \(\varepsilon _2\)-cell problem. The condition \(\left\langle \tilde{{\varvec{\chi }}}\right\rangle _{{\varvec{\zeta }}} = 0\) is imposed in order to guarantee uniqueness.

  3. (iii)

    To \(O(\varepsilon ^2_2)\), applying the average operator \(\left\langle \bullet \right\rangle _{{\varvec{\zeta }}}\) and taking into account the \({\varvec{\zeta }}\) periodicity of the involved functions,

    $$\begin{aligned} \left( \frac{\partial }{\partial x_j} + \varepsilon ^{-1}_1\frac{\partial }{\partial \eta _j}\right) \check{C}^{\varepsilon }_{ijkl}\tilde{U}^{0}_{kl} = 0 \quad \mathrm{in} \quad \Omega ^{\varepsilon _1}_1, \end{aligned}$$
    (16)

    where

    $$\begin{aligned} \check{C}^{\varepsilon }_{ijkl} = \left\langle C^{\varepsilon }_{ijkl} + C^{\varepsilon }_{ijpq}\xi ^{\zeta }_{pqkl}(\tilde{{\varvec{\chi }}})\right\rangle _{{\varvec{\zeta }}} \end{aligned}$$
    (17)

    is the effective stiffness tensor at the\(\varepsilon _1\)-structural level. Note that the derivative in (16) depends on the small parameter \(\varepsilon _1\) and \(\check{\mathbf{ C}}^{\varepsilon } = \check{\mathbf{ C}}^{\varepsilon }(\mathbf{ x},{\varvec{\eta }})\).

Step 2 :

Using (7) in (16) and equating in powers of \(\varepsilon _1\).

  1. (i)

    To \(O(\varepsilon ^0_1)\), we have

    $$\begin{aligned}&\frac{\partial }{\partial \eta _j}\left( \check{C}^\varepsilon _{ijkl}\xi ^\eta _{kl}(\mathbf{ u}^0)\right) = 0 \quad \mathrm{in}~\quad Y\setminus \Gamma _\eta , \end{aligned}$$
    (18)
    (19)
    (20)

    Again the solvability condition is applied to (18)–(20), to obtain

    $$\begin{aligned} \mathbf{ u}^0 = \mathbf{ u}^0(\mathbf{ x}). \end{aligned}$$
  2. (ii)

    To \(O(\varepsilon _1)\), using the fact that \(\xi ^\eta _{kl}(\mathbf{ u}^0) = 0\) and applying the \(\zeta \) average operator,

    $$\begin{aligned}&\frac{\partial }{\partial \eta _j}\left( \check{C}^\varepsilon _{ijkl}\xi ^\eta _{kl}(\mathbf{ u}^1)\right) = -\frac{\partial }{\partial \eta _j}\left( \check{C}^\varepsilon _{ijkl}\xi ^x_{kl}(\mathbf{ u}^0)\right) . \end{aligned}$$

    By the \({\varvec{\eta }}\)-periodicity of \(\check{\mathbf{ C}}^{\varepsilon }\) and the solvability condition, the above equation has a \({\varvec{\eta }}\)-periodic solution which is unique up to an additive constant. In particular, since the problem is linear and \(\mathbf{ u}^0\) does not depend on \({\varvec{\eta }}\),

    $$\begin{aligned}&u^1_i(\mathbf{ x},{\varvec{\eta }}) = \chi _{ikl}(\mathbf{ x},{\varvec{\eta }})\xi ^{x}_{kl}(\mathbf{ u}^0(\mathbf{ x})), \end{aligned}$$
    (21)

    where the third rank tensor \({\varvec{\chi }}\) is \({\varvec{\eta }}\)-periodic and solution of

    $$\begin{aligned}&\frac{\partial }{\partial \eta _j}\left( \check{C}^\varepsilon _{ijkl} + \check{C}^\varepsilon _{ijpq}\xi ^\eta _{pqkl}({\varvec{\chi }})\right) = 0 \quad \mathrm{in}\quad Y\setminus \Gamma _\eta , \end{aligned}$$
    (22)
    (23)
    (24)

    Equations (22)–(24) represent the \(\varepsilon _1\)-cell problem. The condition \(\left\langle {\varvec{\chi }}\right\rangle _{{\varvec{\eta }}} = 0\) is imposed for guarantee uniqueness.

  3. (iii)

    To \(O(\varepsilon ^2_1)\), applying the average operator \(\left\langle \bullet \right\rangle _{{\varvec{\eta }}}\) and taking into account the \({\varvec{\eta }}\) periodicity of the functions involved. The homogenized problem becomes

    $$\begin{aligned} (\mathbf{ P}_h) {\left\{ \begin{array}{ll} \frac{\partial }{\partial x_j}\left( \hat{C}_{ijkl}\xi ^x_{kl}(\mathbf{ u}^0)\right) = 0 &{} \mathrm{in}\quad \Omega ,\\ u^0_i = u^*_i &{} \mathrm{on}~\partial \Omega _d,\\ \hat{C}_{ijkl}\xi ^x_{kl}(\mathbf{ u}^0)n_j = S^*_i &{} \mathrm{on}~\partial \Omega _n, \end{array}\right. } \end{aligned}$$

    where

    $$\begin{aligned} \hat{C}_{ijkl} = \left\langle \check{C}^{\varepsilon }_{ijkl} + \check{C}^{\varepsilon }_{ijpq}\xi ^{\eta }_{pqkl}({\varvec{\chi }})\right\rangle _{{\varvec{\eta }}} \end{aligned}$$
    (25)

    is the effective stiffness tensor.

4 Out-of-plane shear mechanical response

Since we are considering uniaxially aligned fibers, the three-dimensional cell problems can be equivalently formulated as two-dimensional problems over the cross-section of the cell. That is, by symmetry the auxiliary third rank tensors \(\tilde{{\varvec{\chi }}}\) and \({\varvec{\chi }}\) do not depend on \(\zeta _3\) and \(\eta _3\), respectively. Therefore, we can refer to the spatial coordinates vectors as \({\varvec{\eta }}= (\eta _1,\eta _2)\), \({\varvec{\zeta }}= (\zeta _1,\zeta _2)\) (keeping the same notation for the sake of simplicity), and the third components of the normal vectors \(\mathbf{ n}_{{\varvec{\zeta }}}\) and \(\mathbf{ n}_{{\varvec{\eta }}}\) reduce to zero, see also the appendix reported in [19].

We assume that \(\mathbf{ C}^{\varepsilon }\) is piecewise constant, such that, the parametric dependence of the \(\varepsilon _2\)-cell problem on the variables \({\varvec{\eta }}\) and \(\mathbf{ x}\) is lost and \(\tilde{{\varvec{\chi }}}\) depends only on \({\varvec{\zeta }}\). As a consequence, \(\check{\mathbf{ C}}^{\varepsilon }\) is also piecewise constant (as it is averaged on \({\varvec{\zeta }}\)), and therefore \({\varvec{\chi }}\) is depending only on \({\varvec{\eta }}\), so that finally also \(\hat{\mathbf{ C}}\) is piecewise constant.

Applying the above mentioned dimensional reduction, and the fact that \(\mathbf{ C}^{\varepsilon }\) and \(\check{\mathbf{ C}}^{\varepsilon }\) are piecewise constants, the differential problems (13)–(15), (22)–(24) can be rewritten as

(26)

and

(27)

respectively, with \(j,q = 1,2\) and \(i,k,l,p = 1,2,3\). In (26) and (27), \(\tilde{Y}_{\gamma }\) and \(\tilde{Z}_{\gamma }\) (\(\gamma =1,2\)), denote the two-dimensional unit cells at the \(\varepsilon _1\)- and \(\varepsilon _2\)-structural levels, respectively, with restrictions to the matrix (\(\gamma = 1\)) and fiber (\(\gamma = 2\)). The interface curves between the constituents \(\tilde{Y}_1\), \(\tilde{Y}_2\) and \(\tilde{Z}_1\), \(\tilde{Z}_2\) are denoted by \(\tilde{\Gamma }_\eta \) and \(\tilde{\Gamma }_\zeta \), respectively. Moreover, \(C^{\gamma ,\eta }_{ijkl}\) and \(C^{\gamma ,\zeta }_{ijkl}\) are the stiffness tensors of the constituent \(\gamma \) at the \(\varepsilon _1\)- and \(\varepsilon _2\)-structural levels, respectively. In particular, the stiffness tensor of the composite fiber at the \(\varepsilon _1\) structural level is \(C^{2,\eta }_{ijkl} = \check{C}_{ijkl}\).

We further assume that the constituents at the \(\varepsilon _2\) level are isotropic, therefore the fiber phase at the \(\varepsilon _1\)-structural level can be at most monoclinic (i.e. 13 independent elastic coefficients), see, e.g. [15, 16]. In our case, it is however tetragonal symmetric (6 independent elastic coefficients), as we are dealing with square-symmetric arrangement of cylindrical fibers (the cell’s cross section corresponds to a square embedding a circle, see also [15, 27]). In particular, the following relationships hold for both structural levels:

$$\begin{aligned} C^{\zeta }_{1313} = C^{\zeta }_{2323},\quad C^{\eta }_{1313} = C^{\eta }_{2323}, \end{aligned}$$
(28)

and, as both \(\mathbf{ C}^{\varepsilon }\) and \(\check{\mathbf{ C}}^{\varepsilon }\) are in particular orthotropic

$$\begin{aligned} C^{\zeta }_{1323} = C^{\zeta }_{2313}=0,\quad C^{\eta }_{1323} = C^{\eta }_{2313}=0. \end{aligned}$$
(29)

Here we focus on the shear mechanical response related to the third (out-of-plane) component of the elastic displacement. For a generic monoclinic material, the relevant constitutive relations are [15]

$$\begin{aligned} \sigma _{13}&= 2C_{1313}\xi _{13} + 2C_{1323}\xi _{23}, \end{aligned}$$
(30)
$$\begin{aligned} \sigma _{23}&= 2C_{2313}\xi _{13} + 2C_{2323}\xi _{23}, \end{aligned}$$
(31)

where \(\sigma _{13}\) and \(\sigma _{23}\) are the out-of-plane shear stresses and \(\xi _{13}\) and \(\xi _{23}\) are the shear strains. In our case, the resulting effective stiffness \(\hat{\mathbf{ C}}\) is still expected to be at most monoclinic (as the individual phases are tetragonal and the fibers are uniaxially aligned also on the \(\varepsilon _1\)-structural level).

We then aim at obtaining the effective elastic coefficients related to relationships (30) and (31), to characterize the out-of-plane shear mechanical response. This can be done by performing a standard decomposition of the problems (26) and (27) into in-plane and antiplane problems. Exploiting (28) and (29), and fixing \(i,p=3\) in (26) and (27), the resulting nontrivial anti-plane cell problems can be expressed in terms of the doubly periodic functions \(\tilde{\chi }^\gamma _{33\alpha } = \tilde{\chi }^\gamma _{\alpha }({\varvec{\zeta }})\) for \({\varvec{\zeta }}\in \tilde{Z}_{\gamma }\) and \(\chi ^\gamma _{33\alpha } = \chi ^\gamma _{\alpha }({\varvec{\eta }})\) for \({\varvec{\eta }}\in \tilde{Y}_{\gamma }\) as follows [15, 27]

(32)

and

(33)

with \(\alpha =1,2\). Once solved the cell problem (32), the relevant effective coefficients at the \(\varepsilon _1\) structural level are computed by

$$\begin{aligned} \check{C}_{\alpha 3\alpha 3}= & {} \left\langle C^{\zeta }_{\alpha 3\alpha 3} + C^{\zeta }_{\alpha 3\alpha 3}\frac{\partial \tilde{\chi }_\alpha }{\partial \zeta _\alpha }\right\rangle _{{\varvec{\zeta }}},\end{aligned}$$
(34)
$$\begin{aligned} \check{C}_{1323}= & {} \left\langle C^{\zeta }_{2323}\frac{\partial \tilde{\chi }_1}{\partial \zeta _2}\right\rangle _{{\varvec{\zeta }}},\end{aligned}$$
(35)
$$\begin{aligned} \check{C}_{2313}= & {} \left\langle C^{\zeta }_{1313}\frac{\partial \tilde{\chi }_2}{\partial \zeta _1}\right\rangle _{{\varvec{\zeta }}}. \end{aligned}$$
(36)

Solving (33), the effective coefficients are given by

$$\begin{aligned} \hat{C}_{\alpha 3\alpha 3}= & {} \left\langle \check{C}_{\alpha 3\alpha 3} + \check{C}_{\alpha 3\alpha 3}\frac{\partial \chi _\alpha }{\partial \eta _\alpha }\right\rangle _{{\varvec{\eta }}},\end{aligned}$$
(37)
$$\begin{aligned} \hat{C}_{1323}= & {} \left\langle \check{C}_{2323}\frac{\partial \chi _1}{\partial \eta _2}\right\rangle _{{\varvec{\eta }}},\end{aligned}$$
(38)
$$\begin{aligned} \hat{C}_{2313}= & {} \left\langle \check{C}_{1313}\frac{\partial \chi _2}{\partial \eta _1}\right\rangle _{{\varvec{\eta }}}. \end{aligned}$$
(39)

Since we assume square-symmetry also on the \(\varepsilon _1\) structural level, the resulting effective stiffness tensor is actually expected to exhibit tetragonal symmetry, so that in particular

$$\begin{aligned} \hat{C}_{1313}=\hat{C}_{2323}; \quad \hat{C}_{1323}=\hat{C}_{2313}=0, \end{aligned}$$
(40)

as also shown by the results that follow. The effective shear mechanical response is then completely characterized by the effective out-of-plane shear modulus\(\hat{C}_{1313}\).

5 Results and discussion

The theory of analytical functions in [13] can be applied to solve the cell problems (32) and (33), where doubly periodic harmonic functions need to be found (See “Appendix A”). In order to compute the effective properties at both structural levels, it is necessary to truncate the systems (46) and (47) into appropriate orders. Then,

$$\begin{aligned} \check{C}_{1313} - \mathrm {i}\check{C}_{2313}= & {} C^{1,\zeta }_{1313}\left( 1-2\pi \bar{\tilde{a}}_1\right) ,\end{aligned}$$
(41)
$$\begin{aligned} \check{C}_{1323} - \mathrm {i}\check{C}_{2323}= & {} -C^{1,\zeta }_{1313}\left( 1+2\pi \bar{\tilde{a}}_1\right) \mathrm {i},\end{aligned}$$
(42)
$$\begin{aligned} \hat{C}_{1313} - \mathrm {i}\hat{C}_{2313}= & {} C^{1,\eta }_{1313}\left( 1-2\pi \bar{a}_1\right) ,\end{aligned}$$
(43)
$$\begin{aligned} \hat{C}_{1323} - \mathrm {i}\hat{C}_{2323}= & {} -C^{1,\eta }_{1313}\left( 1+2\pi \bar{a}_1\right) \mathrm {i}, \end{aligned}$$
(44)

where \(\bar{a}_1\) (\(\bar{\tilde{a}}_1\)) denotes the conjugate of the complex coefficient \(a_1\) (\(\tilde{a}_1\)) and “\(\mathrm {i}\)” is the imaginary unit.

Using formulas (41)–(44) the effective coefficients at both structural levels can be found. For the sake of exemplifying, we choose the following material properties \(C^{1,\zeta }_{1313} = 1\), \(C^{2,\zeta }_{1313} = 10\) and \(C^{1,\eta }_{1313} = 5\), and made a parametric study by varying the volume fraction of the fiber at both structural levels. Particularly, the effective coefficients are computed for the same fiber volume fraction at each structural level, i.e. \(\phi = \phi _{{\varvec{\zeta }}} = \phi _{{\varvec{\eta }}}\). Then, we proceed in the following way:

  1. 1.

    Given the properties \(C^{1,\zeta }_{1313}\) and \(C^{2,\zeta }_{1313}\) and for a fixed volume fraction of \(\tilde{Z}_2\), denoted by \(\phi _{{\varvec{\zeta }}}\), the cell problem at the \(\varepsilon _2\)-structural level (32) is solved. To find the coefficient \(\tilde{a}_l\), the infinite linear system (46) is truncated at a certain order \(\tilde{K}\) and solved. The matrix \(\mathbf{ W}_k^{{\varvec{\zeta }}}\) is written in terms of \(\phi _{{\varvec{\zeta }}}\).

  2. 2.

    To compute the effective coefficients \(\check{C}_{1313}\), \(\check{C}_{1323}\), \(\check{C}_{2313}\) and \(\check{C}_{2323}\) of the composite fiber \(\Omega _2^{\varepsilon _1}\), the solution \(\tilde{a}_l\) of the linear system is substituted in (41) and (42).

  3. 3.

    Now, the cell problem at the \(\varepsilon _1\)-structural level (33) is solved. In particular, we only need to fix \(C^{1,\eta }_{1313}\) since \(C^{2,\eta }_{1313} = \check{C}_{1313}\) was found in the previous step. At this point the volume fraction of the fiber \(\tilde{Y}_2\) must be fixed. One way to proceed is to make \(\phi _{{\varvec{\eta }}} = \phi _{{\varvec{\zeta }}}\).

  4. 4.

    Finally, to find \(a_l\), and consequently the effective coefficients \(\hat{C}_{1313}\), \(\hat{C}_{1323}\), \(\hat{C}_{2313}\) and \(\hat{C}_{2323}\), the infinite linear system (47) is truncated at a certain order K and solved. In this case, the matrix \(\mathbf{ W}_k^{{\varvec{\eta }}}\) is equal to \(\mathbf{ W}_k^{{\varvec{\zeta }}}\), which is already computed.

Figure 2 presents the values obtained for the effective coefficients \(\check{C}_{1313}\) (left) and \(\hat{C}_{1313}\) (right) as a function of the fiber volume fraction. Specifically, the truncation order of the systems was fixed to \(\tilde{K} = K = 3\), thus, decreasing the computational cost. As a consequence of constituent’s isotropic behavior, we obtain \(\check{C}_{1313} = \check{C}_{2323}\), \(\hat{C}_{1313} = \hat{C}_{2323}\) and \(\check{C}_{2313} = \check{C}_{1323} = \hat{C}_{2313} = \hat{C}_{1323} = 0\). A comparison between the results by the three scales asymptotic homogenization method and the finite element method using FreeFEM++ is also shown in Fig. 2. Specifically, we approximate the involved functions by piecewise linear continuous finite elements. As observed, the curves overlap even when the truncation orders of the infinite linear systems are very small. Interestingly, for the particular set of parameters fixed, the effective behavior of \(\hat{C}_{1313}\) (in the context of elasticity \(\hat{C}_{1313}\) is the effective shear modulus \(\hat{\mu }\)) behaves as a quadratic curve in function of the fiber volume fraction. This behavior is a consequence of the fact that at the \(\varepsilon _2\)-structural level the fibers are stiffer than the host medium, and at the \(\varepsilon _1\)-structural level the matrix becomes the stiffer constituent. In several works similar patterns have been observed. For instance, the enhancement of the effective out-of-plane Young modulus was obtained in [24] for a periodic bilaminate, and in [31], for a particular type of composite material.

Fig. 2
figure 2

Effective out-of-plane shear moduli \(\check{C}_{1313}\) (formula (41)) (left) and \(\hat{C}_{1313}\) (formula (43)) (right) plotted against the fiber volume fraction. Comparisons with FEM are also shown

Full size image

6 Concluding remarks

In the present work, the effective behavior of hierarchical linear elastic composites at different length scales was studied. The approach permits the study of problems where several length scales are present (the two-scale asymptotic homogenization only deals with two different length scales). The novelty of this work relies in the solution, for the first time, of the effective elastic shear stiffness considering a nested arrangement of cylindrical and uniaxially aligned fibers. The corresponding cell problems are solved analytically using complex variables and the results are compared with a finite element approach. Since analytical formulas are found for computing the effective coefficients the computational cost is very low.

Future developments of this work will concern the analysis of the in-plane problems [16, 27] to fully characterize the effective mechanical response of hierarchical three-scale materials. Moreover, the extension of the present model to interface debonding conditions (see, e.g. [23]), as well as geometric heterogeneities (for example generalizing the non-macroscopically uniform homogenization approach developed in [8, 17, 18]) will provide more general and realistic results applicable to real-world hierarchical composites. The current method represents a first step towards computationally feasible multiscale modeling of complex hierarchical materials. For example, this approach could be exploited to model musculoskeletal mineralized tissues (such as bone and tendons) which are organized across several spatial scales. In this context, the three scales would represent the arragement on the basic constituents (i.e. collagen and mineral crystals), the resulting mineralized collagen fibril, and finally their packing into the mineralized collagen fibril bundle. Since the model is developed for fiber-reinforced composites, it can then serve as an approximation for both fibers embedded in a matrix, and for fusing inclusions of reinforcing material, such as for example the hydroxyapatite mineral crystals which are found in the aged bone tissue (see, e.g. [22]).