Abstract
We analyze competition through incentive contracts for managers in duopoly. Privately informed managers exert surplus enhancing effort that generates an externality on the rival. Asymmetric information on imperfectly correlated shocks creates a two-way distortion of efforts under strategic substitutability in effort and a double downward distortion under strategic complementarity in effort. In the first case, as with contracts for R&D activity or small contractual spillovers for quantity and price competition, increasing the correlation of types reduces the polarization of contracts and the differentials in managerial compensations between efficient and inefficient managers. In the second case, as with large contractual spillovers, the opposite occurs.


Similar content being viewed by others
Notes
Even the relation with external partners, such as exclusive dealers or upstream firms, can be governed by incentive contracts that affect (and are affected by) competition.
The same focus on moral hazard applies in the analysis by Baggs and de Bettignies (2007).
More recently Piccolo and Pagnozzi (2013) have found a two-way distortion in a model of information sharing between competing hierarchies when traded goods are substitutes.
In what follows we assume that the appropriate second order conditions are satisfied.
As is well known, strategic delegation can be used by each firm to affect the equilibrium outcomes, but we will not focus on this issue.
This contracting limitation may be due to problems of verifiability on the other firm’s variables for lack of auditing rights and abilities—see Brainard and Martimort (1996).
The denominator is always positive in case of strategic substitutability. We assume \(\Pi _{12}\left( e_{1}^{*},e_{1}^{*}\right) <g_{ee}\left( \theta _{1},e_{1}^{*}\right) /\lambda -\left( 1/\lambda -1\right) \Pi _{11}\left( e_{1}^{*},e_{2}^{*}\right) -\Pi _{11}\left( e_{1}^{*},e_{1}^{*}\right) \) in case of strategic complementarity. This is easily satisfied in our example.
Biglaiser and Mezzetti (2000) have considered auctions to hire managers in a principal-agent framework. With identical principals, the equilibrium gives all the surplus to each type of worker.
As mentioned before we always assume that firm i’s contract cannot be conditioned on the type of the manager of firm j or, more generally, on messages sent from that firm. The literature on competing mechanisms has investigated equilibria of this kind in different frameworks—see, for a survey, Dittrich and Städter (2015).
More efficient solutions to the moral hazard problem could be reached by changing the ownership structure and selling the right to control to the manager. However wealth constraints make this solution often unrealistic (see Lewis and Sappington 2000, for a general treatment), and we will not consider it here.
We can check later that the solution is monotonic, which guarantees global incentive compatibility. There is no need for a modified monotonicity condition as in Piccolo et al. (2008) because here incentives constraint are not modified by contract competition.
However, if goods are complements, strategic complementarity between efforts emerges.
Again, we exclude the possibility of conditioning contracts on messages from the other manager. As is well known since Crémer and McLean (1985), this would allow principals to exploit correlation in a more efficient way - see Bertoletti and Poletti (1997) and Laffont and Martimort (2000) for related applications. However, in our context, contracts based on effort of other managers do not appear realistic.
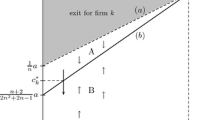
The generalized slopes \(h_{e}\left( e_{2},\theta _{2},\theta _{1},\alpha \right) \) and \(f_{e}\left( e_{2},\theta _{1},\alpha \right) \) satisfy \( \left| h_{e}\left( e_{2},\theta _{2},\theta _{1},\alpha \right) \right| >\left| f_{e}\left( e_{2},\theta _{1},\alpha \right) \right| \). Notice that \(f_{e}\left( e_{2},\theta _{1},\overline{\alpha } \right) =0\) and \(h_{e}\left( e_{2},\theta _{2},\theta _{1},\overline{\alpha } \right) \rightarrow \infty \).
We are grateful to an anonymous referee for suggesting the proofs by contradiction.
References
Aggarwal RK, Samwick AA (1999) The other side of the trade-off: the impact of risk on executive compensation. J Polit Econ 107(1):65–105
Aggarwal RK, Samwick AA (1999) Executive compensation, strategic competition, and relative performance evaluation: theory and evidence’. J Financ 54(6):1999–2043
Baggs J, de Bettignies J-E (2007) Product market competition an agency costs. J Ind Econ 55(2):289–323
Baron D, Myerson R (1982) Regulating a monopolist with unknown costs. Econometrica 50(4):911–930
Bernheim BD, Whinston MD (1986) Common Agency. Econom 54(4):923–942
Bertoletti P, EtroF (2016) Preferences, entry and market structure. RAND J Econ (in press)
Bertoletti P, Poletti C (1997) X-inefficiency, competition and market information. J Ind Econ 45(4):359–375
Biglaiser G, Mezzetti C (2000) Incentive auctions and information revelation. RAND J Econ 31(1):145–164
Brainard SL, Martimort D (1996) Strategic Trade policy design with asymmetric information and public contracts. Rev Econ Stud 63:81–105
Calzolari G, Scarpa C (2012) On regulation and competition: pros and cons of a diversified monopolist, WP 55, Fondazione Eni Enrico Mattei
Crémer J, McLean RP (1985) Optimal selling strategies under uncertainty for a discriminating monopolist when demands are interdependent. Econometrica 53(2):345–361
d’Aspremont C, Gerard-Varet C (1979) Incentives and incomplete information. J Public Econ 11(1):25–45
Demougin D, Helm C (2006) Moral hazard and bargaining power. Germ Econ Rev 7(4):463–470
Dittrich M, Städter M (2015) Moral hazard and bargaining over incentive contracts. Res Econ 69(1):75–85
Etro F (2011) Endogenous Market structures and contract theory: delegation, principal-agent contracts, screening, franchising and tying. Eur Econ Rev 55(4):463–479
Etro F, Cella M (2013) Equilibrium principal-agent contracts: competition and R&D incentives. J Econ Manag Strat 22(3):488–512
Gabaix X, Landier A (2008) Why has CEO pay increased so much? Q J Econ 123:49–100
Hotelling H (1929) Stability in competition. Econ J 39:41–57
Jensen M, Murphy K (1990) Performance pay and top-management incentives. J Polit Econ 98(2):225–264
Karuna C (2007) Industry product market competition and managerial incentives. J Account Econ 43(2–3):275–297
Laffont J-J, Martimort D (2000) Mechanism design with collusion and correlation. Econometrica 68(2):309–342
Laffont J-J, Tirole J (1993) A theory of incentives in procurement and regulation. MIT Press, Cambridge
Laffont J-J, Tirole J (1986) Using cost observation to regulate firms. J Polit Econ 94(3):614–641
Lazear (2015) The impatient salesperson and the delegation of pricing authority. Res Econ 69(1):63–74
Ledyard J, Palfrey TR (1999) A characterization of interim efficiency with public goods. Econometrica 67(2):435–448
Lewis TR, Sappington DEM (1989) Countervailing incentives in agency problems. J Econ Theory 49(2):294–313
Lewis TR, Sappington DEM (2000) Motivating wealth-constrained actors. Am Econ Rev 90(4):944–960
Martimort D (1996) Exclusive dealing, common agency, and multiprincipal incentive theory. RAND J Econ 27(1):1–31
Murphy KJ (1999) Executive compensation. In: Ashenfelter O, Card D (eds) Handbook of labor economics, vol 38. Elsevier, Oxford, pp 2485–2563
Myerson RB (1982) Optimal coordination mechanisms in generalized principal-agent problems. J Math Econ 10(1):67–81
Peters M (2014) Competing mechanisms. Can J Econ 47(2):373–397
Piccolo S, D’Amato M, Martina R (2008) Product market competition and organizational slack under profit-target contracts. Int J Ind Org 26:1389–1406
Piccolo S, Pagnozzi M (2013) Information sharing between vertical hierarchies. Games Econ Behav 79:201–222
Rosen S (1981) The economics of superstars. Am Econ Rev 71(5):845–858
Author information
Authors and Affiliations
Corresponding author
Additional information
We are thankful to the Editor Giacomo Corneo, and Patrick Rey, Giacomo Calzolari, Salvatore Piccolo, Elena Manzoni, Giovanna Iannantuoni, seminar participants at CSEF (Naples), participants at SAET 2011 (Faro, Portugal), SfED 2011 (Montreal, Canada) and in particular to two referees for useful comments.
Appendix
Appendix
Proof of Proposition 1
To prove \(e_{1}^{*}\ge e_{2}^{*}\) assume, by contradiction, that the opposite holds, that is \(e_{1}^{*}<e_{2}^{*}\).Footnote 18 Then, since \(g_{e\theta }>0\) and \(g_{ee\theta }\ge 0\) by A.1., it must be that:
Moreover, since \(\Pi _{11}\le 0\), it must be that:
which contradicts the previous inequality.
Proof of Proposition 2
To prove \(e_{1}\ge e_{2}\) assume, by contradiction, that the opposite holds, that is \(e_{1}<e_{2}\). Then, since \( g_{e\theta }>0\) and \(g_{ee\theta }\ge 0\) by A.1, it must be that:
which implies:
Moreover, since \(\Pi _{11}\le 0\), it must be that:
which contradicts the previous inequality.
Proof of Proposition 3
Let us consider the following system:
which defines \(\left( e_{1}^{*},e_{2}^{*}\right) \) if \(\mu =0\) and \( \left( e_{1},e_{2}\right) \) if \(\mu =1\). Applying the Cramer rule we have:
where
Notice that for any \(\theta _{2}>\theta _{1}\) we have \(\Phi _{e}\left( e_{2},\theta _{1},\theta _{2}\right) >0\) by A.1 and \(\Delta >0\) by A.2, therefore:
Analogously, we have:
Then, the introduction of asymmetric information with \(\Phi _{e}>0\) implies \( e_{1}>e_{1}^{*}\) and \(e_{2}<e_{2}^{*}\) (the two-way distortion) under strategic substitutability, and \(\left( e_{1},e_{2}\right) <\left( e_{1},e_{2}^{*}\right) \) (double downward distortion) under strategic complementarity.
Proof of Proposition 4
To characterize the comparative statics of the equilibrium effort levels \(\left( e_{1},e_{2}\right) \) with respect to \( \alpha \) when \(\Pi _{12}\left( e_{1},e_{2}\right) <0\) we totally differentiate the equilibrium system:
and apply the Cramer rule as before to obtain:
where again \(\Delta >0\) by A.2. Under strategic substitutability we have:
because \(\Pi _{1}\left( e_{1},e_{2}\right) >\Pi _{1}\left( e_{1},e_{1}\right) \) and \(\Pi _{1}\left( e_{2},e_{2}\right) >\Pi _{1}\left( e_{2},e_{1}\right) \). Analogously we have \(de_{2}/d\alpha >0\).
Proof of Proposition 5
To compare extreme effort levels under the assumption \(\Pi _{12}\left( e_{1},e_{2}\right) >0\), let us consider the effort of the efficient manager first. Notice that \(e_{1}(0)=e_{1}\) as defined in (24):
and \(e_{1}(\overline{\alpha })=e_{11}\) as defined in (13 ):
Strategic complementarity and \(e_{1}>e_{2}\) imply \(\Pi _{1}\left( e_{1},e_{1}\right) >\Pi _{1}\left( e_{1},e_{2}\right) \) and therefore \(e_{1}( \overline{\alpha })=e_{11}>e_{1}(0)=e_{1}\).
Consider the effort of the inefficient manager now. Notice that \( e_{2}(0)=e_{2}\) as defined in (25):
while \(e_{2}(\overline{\alpha })\) must satisfy:
For any \(e_{1}>e_{2}\) strategic complementarity implies \(\Pi _{1}\left( e_{2},e_{1}\right) >\Pi _{1}\left( e_{2},e_{2}\right) \), therefore \( e_{2}=e_{2}(0)>e_{2}(\overline{\alpha })\).
Rights and permissions
About this article
Cite this article
Cella, M., Etro, F. Contract competition between hierarchies, managerial compensation and imperfectly correlated shocks. J Econ 118, 193–218 (2016). https://doi.org/10.1007/s00712-016-0472-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-016-0472-x