Abstract
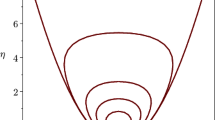
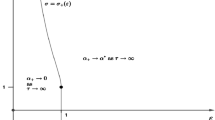
If the coexistence of two phases at the transition temperature is kept under observation for a long time, then one observes that the system is not exactly in equilibrium and a very slow evolution driven by surface tension is taking place. Theoretically, one should eventually see a spatially homogeneous state, but the time for settling down is so long that what one actually observes is “motion towards a stable state.” The complexity of the spatial distribution of the two phases keeps decreasing but appears to be stable for very long periods of time with intermittent periods of fast motion when there are small inclusions of one of the two regions embedded in the other phase. For a simple reaction diffusion model, it is shown that this phenomenon can be explained by investigating the flow on the attractor and the unstable manifolds of equilibria.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Angenent, S. (1988). The zeroset of a solution of a parabolic equation (preprint).
Benassi, A., and Fouque, J. P. (1988). Hydrodynamic limit for asymmetric simple exclusion processes.Ann. Probability 16 (to appear).
Brunovsky, P., and Fiedler, B. (1988a). Connecting orbits in scalar reaction diffusion equations. I. InDynamics Reported, Vol. 1, John Wiley, New York, pp. 57–89.
Brunovsky, P., and Fiedler, B. (1988)b. Connecting orbits in scalar reaction diffusion equations. II.J. Differential Equations (to appear).
Bongiorno, V., Scriven, L. E., and Davis, H. T. (1976). Molecular theory of fluid interfaces.J. Colloid Interface Sci. 57, 462–475.
Carr, J., and Pego, R. L. (1988). Metastable patterns in solutions ofut, =ɛ 2 uxx-f(u).Comm. Pure Appl. Math., (to appear).
Casten, R. C., and Holland, C. J. (1978). Instability results for reaction diffusion equations with Neumann boundary conditions.J. Differential Equations 27, 266–273.
Fusco, G., and Oliva, W. M. (1988). Jacobi matrices and transversality.Proc. R. Soc. Edinburgh (to appear).
Gantmacher, F. R. (1959).The Theory of Matrices, Vol. 2, Chelsea, New York.
Gurtin, M. E. (1986a). On the two-phase Stefan problem with interfacial energy and entropy.Arch. Rational Mech. Anal. 96, 199–241.
Gurtin, M. E. (1986b). On phase transitions with bulk, interfacial, and boundary energy.Arch. Rational Mech. Anal. 96, 243–264.
Hale, J. K. (1988). Asymptotic behavior of dissipative systems.Math. Surv. Monogr. 25.
Henry, D. (1983). Geometric theory of semilinear parabolic equations.Lect. Notes Math., Am. Math. Soc. 840, Springer-Verlag, New York.
Henry, D. (1985). Some infinite-dimensional Morse-Smale systems defined by parabolic partial differential equations.J. Differential Equations 53, 165–205.
Matano, H. (1979). Asymptotic behavior and stability of solutions of semilinear diffusion equations.Publ. Res. Inst. Math. Sci. 15, 401–458.
Matano, H. (1982). Nonincrease of lap-number of a solution for a one-dimensional semilinear parabolic equations.J. Fac. Sci. Univ. Tokyo [Sect. IA] 23, 401–441.
Novick-Cohen, A., and Segal, L. A. (1984). Nonlinear aspects of the Cahn-Hilliard equation.Physica D 10, 278–298.
Presutti, E. (1987). Collective behavior of interacting particle systems. InProceedings of the First World Congress of the Bernoully Society, Tashkent, USSR, September 1986, Vol. 1, VNU Scientific Press, Utrecht, The Netherlands, pp. 295–413.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fusco, G., Hale, J.K. Slow-motion manifolds, dormant instability, and singular perturbations. J Dyn Diff Equat 1, 75–94 (1989). https://doi.org/10.1007/BF01048791
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01048791